Corresponding Angles (Definition, Theorem & Examples)

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What are corresponding angles?

A corresponding angle is one that holds the same relative position as another angle somewhere else in the figure. Corresponding angles in plane geometry are created when transversals cross two lines.

Two angles correspond or relate to each other by being on the same side of the transversal. One is an exterior angle (outside the parallel lines), and one is an interior angle (inside the parallel lines).

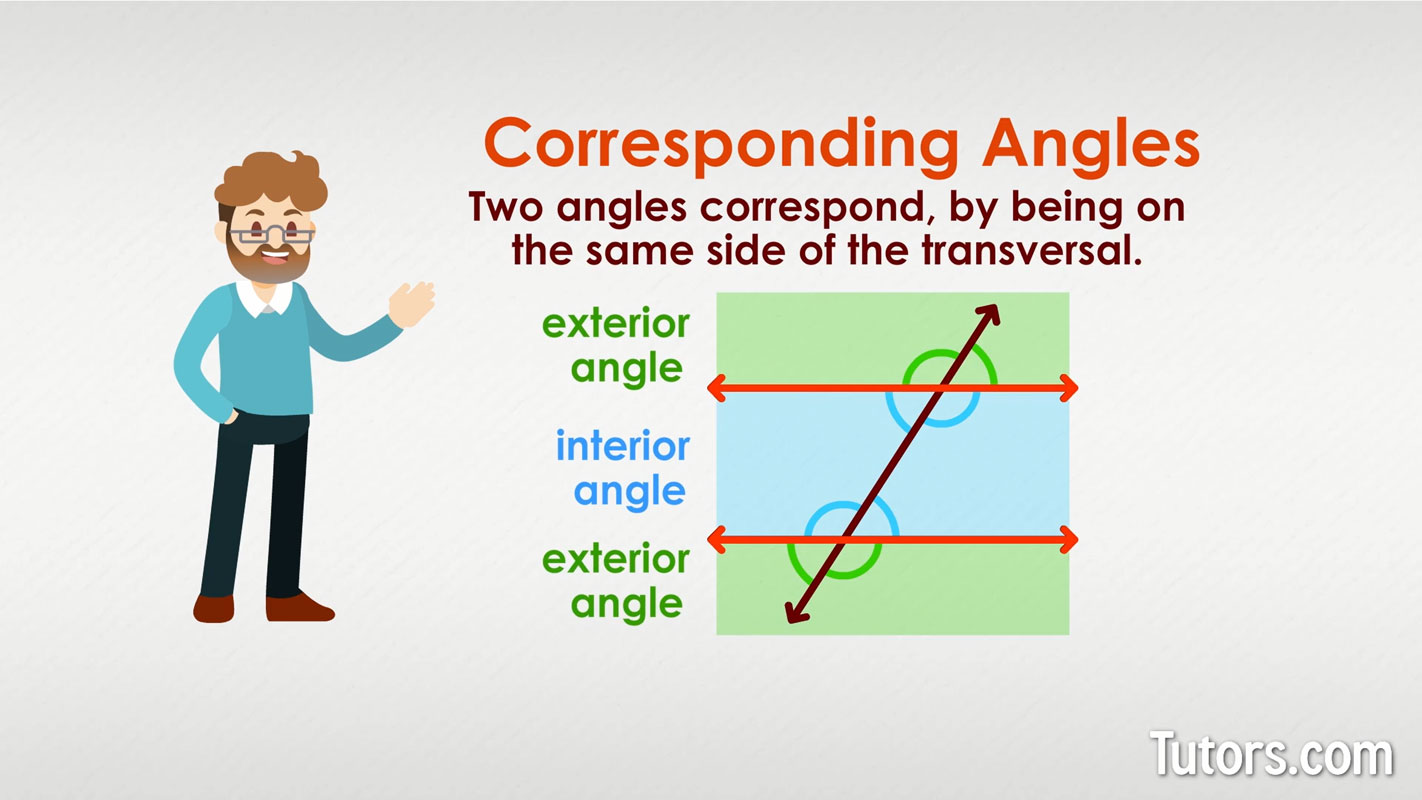
Corresponding angles are just one type of angle pair. Angles that are on the opposite side of the transversal are called alternate angles. You can have alternate interior angles and alternate exterior angles.

Corresponding angles are never adjacent angles. They do not touch, so they can never be consecutive interior angles.

Which angles are corresponding angles?

Can you find the corresponding angle for angle 2 in our figure?

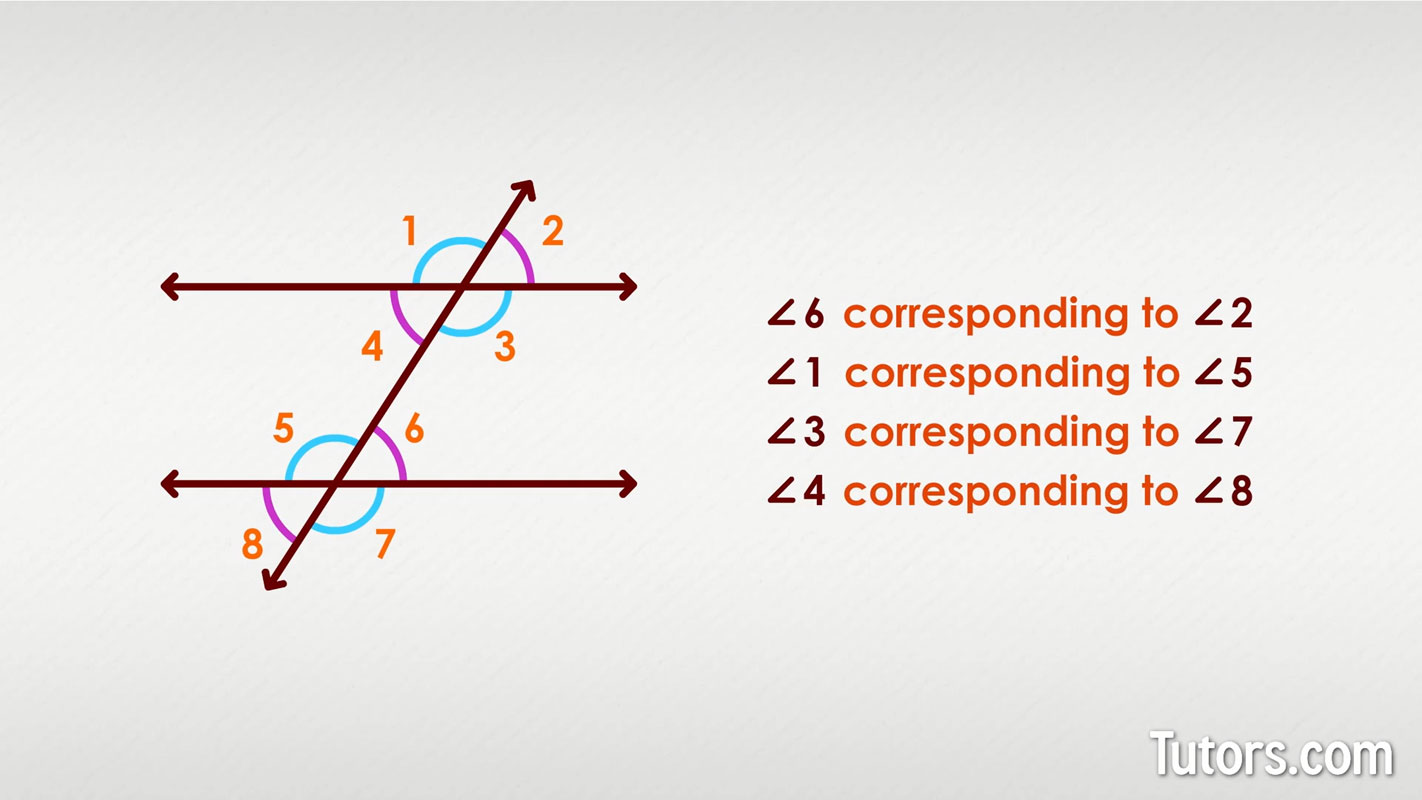
Did you notice angle 6 corresponds to angle 2? They are a pair of corresponding angles. Can you find all four corresponding pairs of angles?

Here are the four pairs of corresponding angles:

1. Angles 1 and 5

2. Angles 2 and 6

3. Angles 3 and 7

4. Angles 4 and 8

Corresponding angles theorem

When a transversal line crosses two lines, eight angles are formed. The Corresponding Angles Theorem says that:

The Corresponding Angles Postulate is simple, but it packs a punch because, with it, you can establish relationships for all eight angles of the figure.

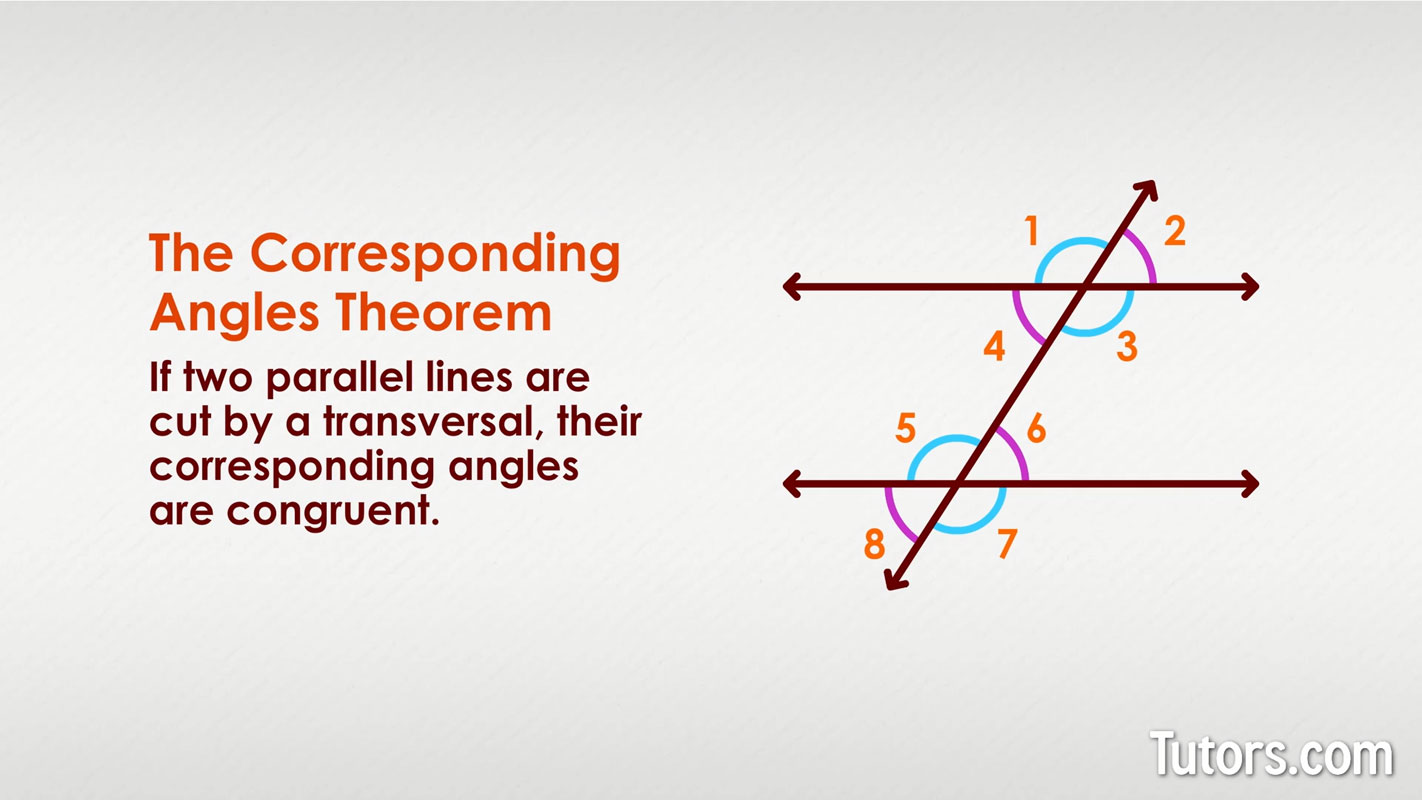
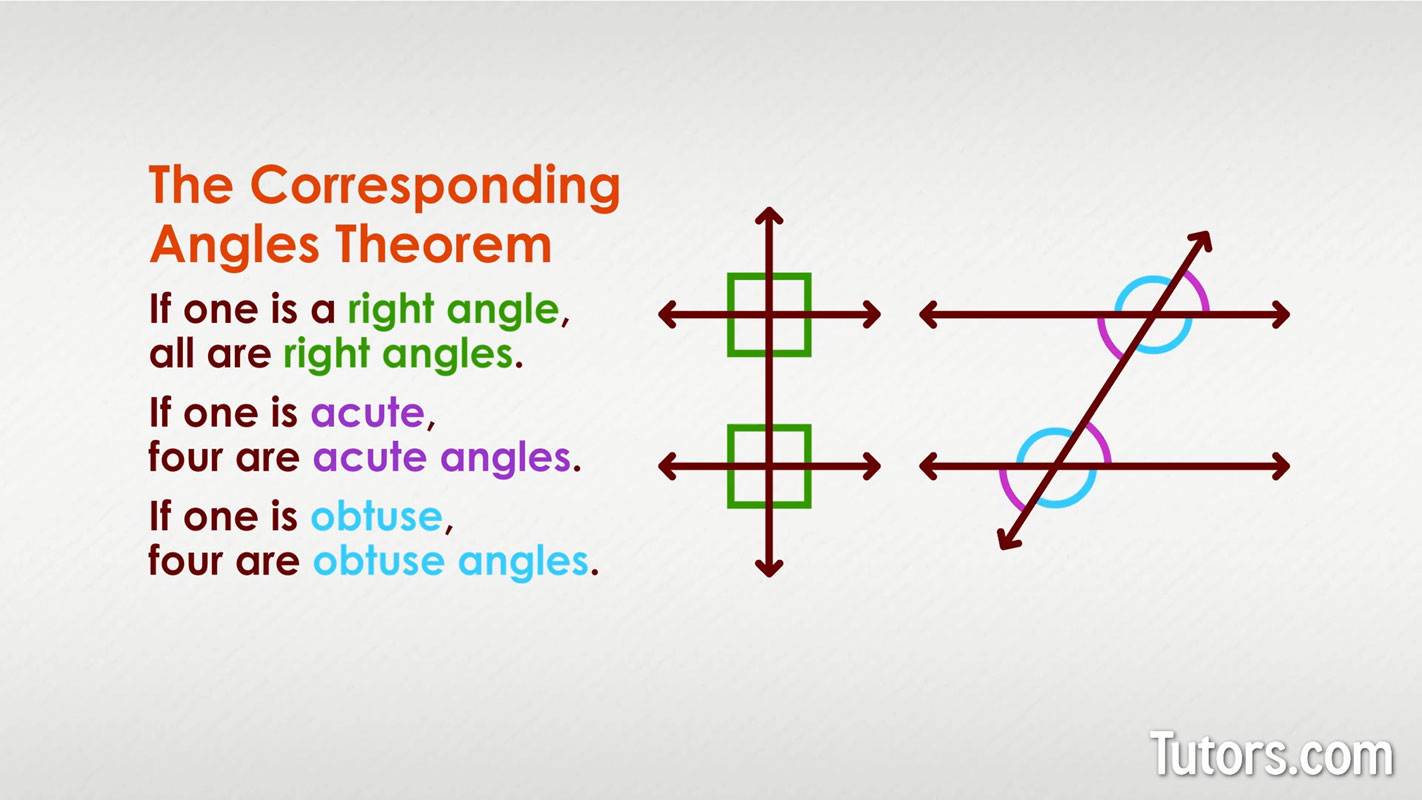
Because of the Corresponding Angles Theorem, you already know several things about the eight angles created by the three lines:

• If one is a right angle, all are right angles

• If one is acute, four are acute angles

• If one is obtuse, four are obtuse angles

• All eight angles can be classified as adjacent angles, vertical angles, and corresponding angles

If you have a two parallel lines cut by a transversal, and one angle (angle 2) is labeled 57°, making it acute, our theorem tells us that there are three other acute angles are formed.

The angles to either side of our 57° angle – the adjacent angles – are obtuse. Angle 3 is a vertical angle to angle 2. They share a vertex and are opposite each other.

Converse of corresponding angles theorem

The converse of the Corresponding Angles Theorem is also interesting:

The converse theorem allows you to evaluate a figure quickly. If you are given a figure similar to our figure below, but with only two angles labeled, can you determine anything by it?

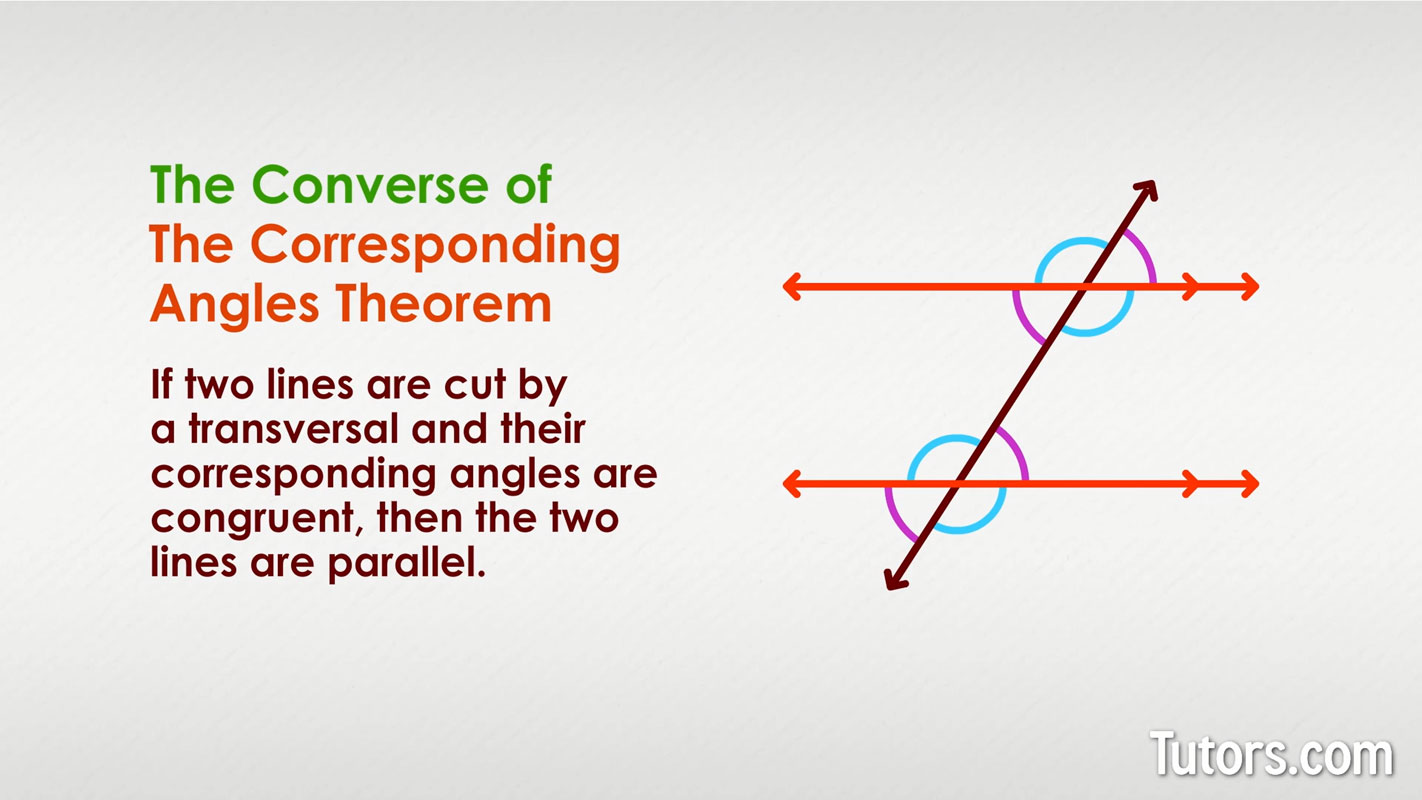
Since the corresponding angles are shown to be congruent, you know that the two lines cut by the transversal are parallel.

If the lines cut by the transversal are not parallel, then the corresponding angles are not equal. They are just corresponding by location.

Corresponding angles examples

1. Looking at our BOLD MATH figure again, and thinking of the Corresponding Angles Theorem, if you know that angle 1 measures 123°, what other angle must have the same measure?

2. You can use the Corresponding Angles Theorem even without a drawing. If two corresponding angles of a transversal across parallel lines are right angles, what do you know about the figure?

3. Can you possibly draw parallel lines with a transversal that creates a pair of corresponding angles, each measuring 181°?

4. Imagine a transversal cutting across two lines. You learn that corresponding angles are not congruent. What does that tell you about the lines cut by the transversal?

And now, the answers (try your best first!):

1. Angle 5 also measures 123°. Because of the vertical angles theorem, angle 4 and 8 and also measure 123°.

2. If two corresponding angles of a transversal across parallel lines are right angles, all angles are right angles, and the transversal is perpendicular to the parallel lines.

3. You cannot possibly draw parallel lines with a transversal that creates a pair of corresponding angles, each measuring 181°.

4. With transversal cutting across two lines forming non-congruent corresponding angles, you know that the two lines are not parallel.