Alternate Interior Angles — Definition, Theorem & Examples
Alternate interior angles
Sometimes geometry feels like a giant parts warehouse. You trade a lot of number-crunching (not much addition, multiplication, subtraction or division in geometry) for a lot of inventory.
To understand alternate interior angles we must understand the parts of an angle and some other key terms.
Parts of an angle
For example, let's construct angle Z. We almost never write "angle Z", using instead a quick shorthand, ∠Z. Something as simple as an angle has parts.
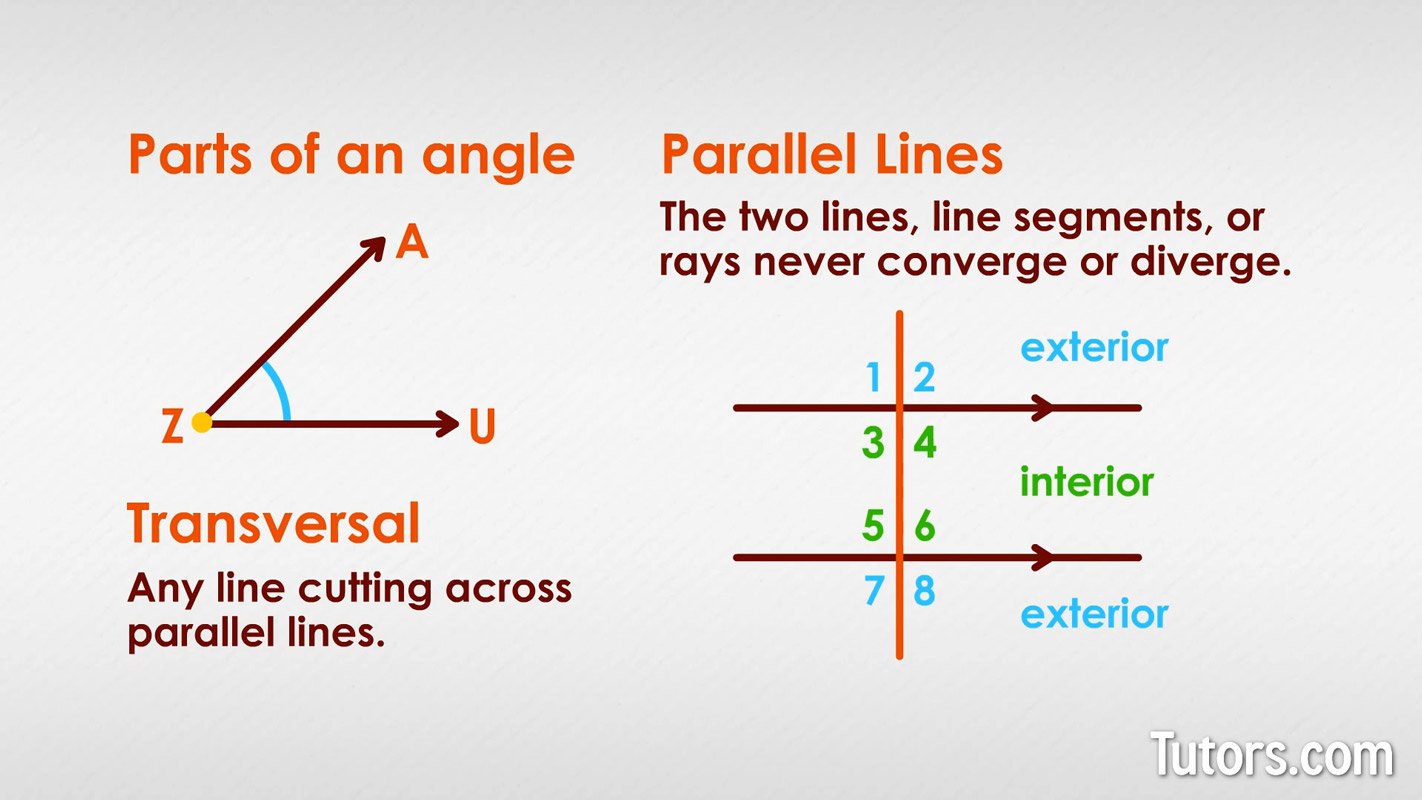
Two rays, ZA and ZU, meet at Point Z
Where they meet at Point Z, they form a vertex, ∠Z
We say rays ZA and ZU, but those rays could also be small snippets out of longer lines that intersected at Point Z. They could be snippets cut as rays or as line segments, depending on taking an infinite chunk or a finite chunk of the infinite, intersecting lines.
Parallel lines
Unlike the intersecting rays ZA and ZU, parallel lines never meet. Parallel lines, line segments, or rays never converge (move closer) or diverge (move away).
The only sneaky way to get an angle from parallel lines is to declare each line is a straight angle, with a measure of 180°. While two points determine a line, if you locate three points on a line, you have created a straight angle with the middle point as the vertex.
Transversals
Parallel lines can be intersected by transversals. Any line cutting across parallel lines is a transversal. It can cross at any angle. A transversal intersecting parallel lines at 90° is perpendicular.
Alternate interior angles definition
When a transversal intersects parallel lines, it creates an interior and exterior. Think about it: if you were two-dimensional and came across a line in your path, that line would stretch infinitely in two directions and you could not get past it. You would be outside, at the exterior, of the parallel lines. Just beyond the line and between it and the parallel line next to it, is the interior.
When the transversal intersects, it creates four angles at each parallel line, or eight angles altogether. Four of those angles are exterior and four are interior. We are interested in the four interior lines, those are our Alternate Interior Angles.
Let's create parallel lines LI and ON, and a transversal HE.
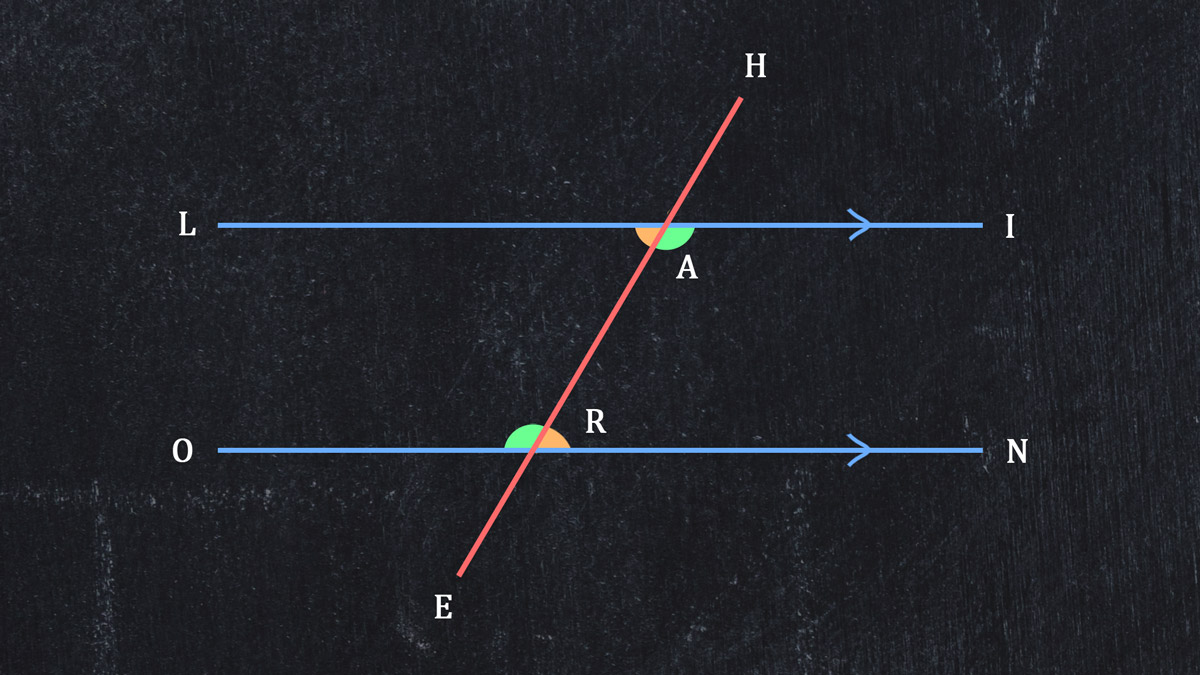
The two points where HE crosses the parallel lines are points A and R. Yes, we have a HARE crossing a LION.
You mark drawings of parallel lines with little bird-feet marks, like Vs on their sides.
Notice, we have four exterior angles:
∠HAL
∠HAI
∠ORE
∠NRE
And, we have four interior angles:
∠LAR
∠IAR
∠ARO
∠ARN
We are only interested in the four interior angles. Two of the interior angles are built using the top parallel line LI, and two are built using the bottom parallel line, ON.
Alternate interior angles are two congruent angles from different parallel lines (one from LI, one from ON). This says:
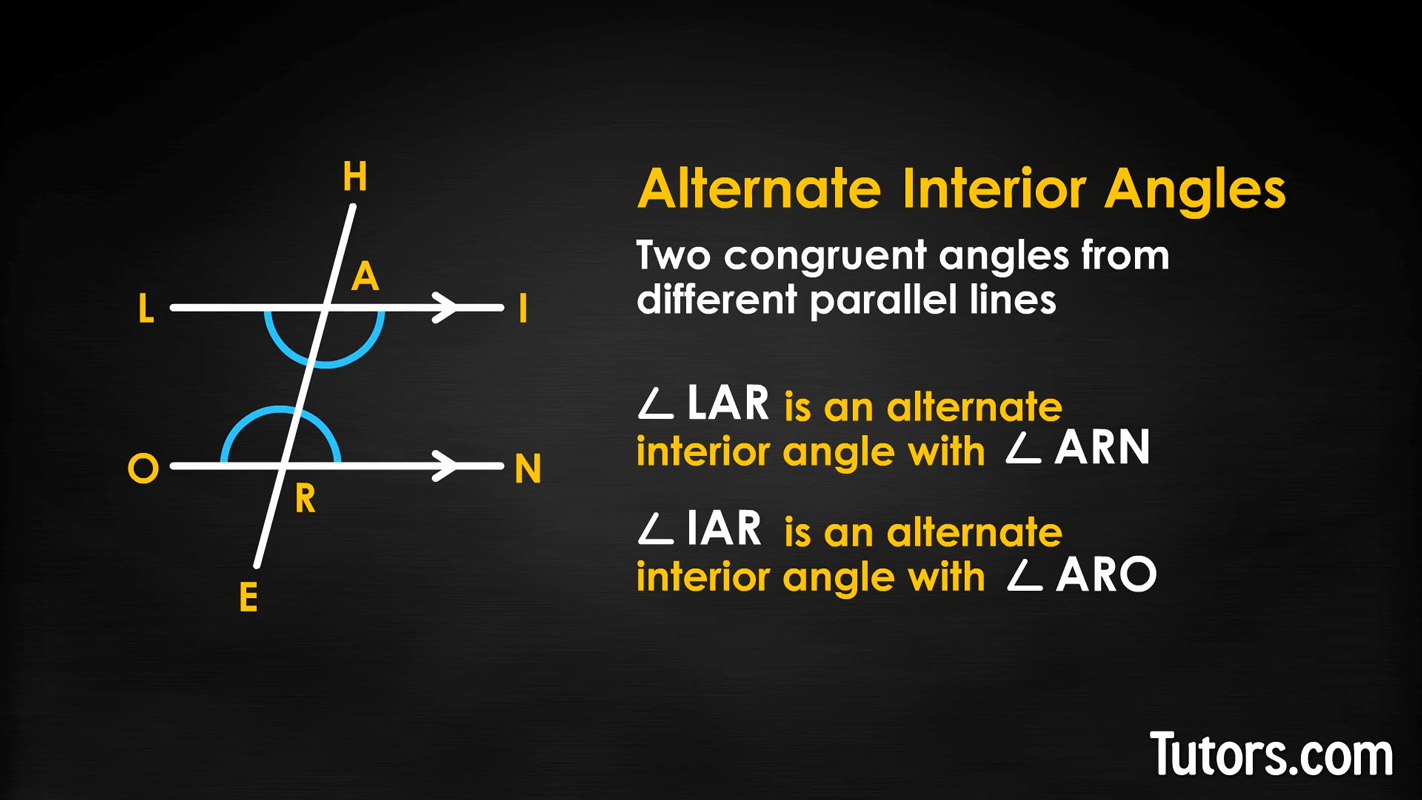
∠LAR is an alternate interior angle with ∠ARN
∠IAR is an alternate interior angle with ∠ARO
Alternate interior angles theorem
The Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

Converse of alternate interior angles theorem
The converse of the alternate interior angles theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
Alternate interior angles examples
We can prove both these theorems so you can add them to your toolbox. With our original figure, LI and ON are parallel lines (given) with the transversal HE (given).
We could declare all sorts of relationships, but the proof can be short and simple:
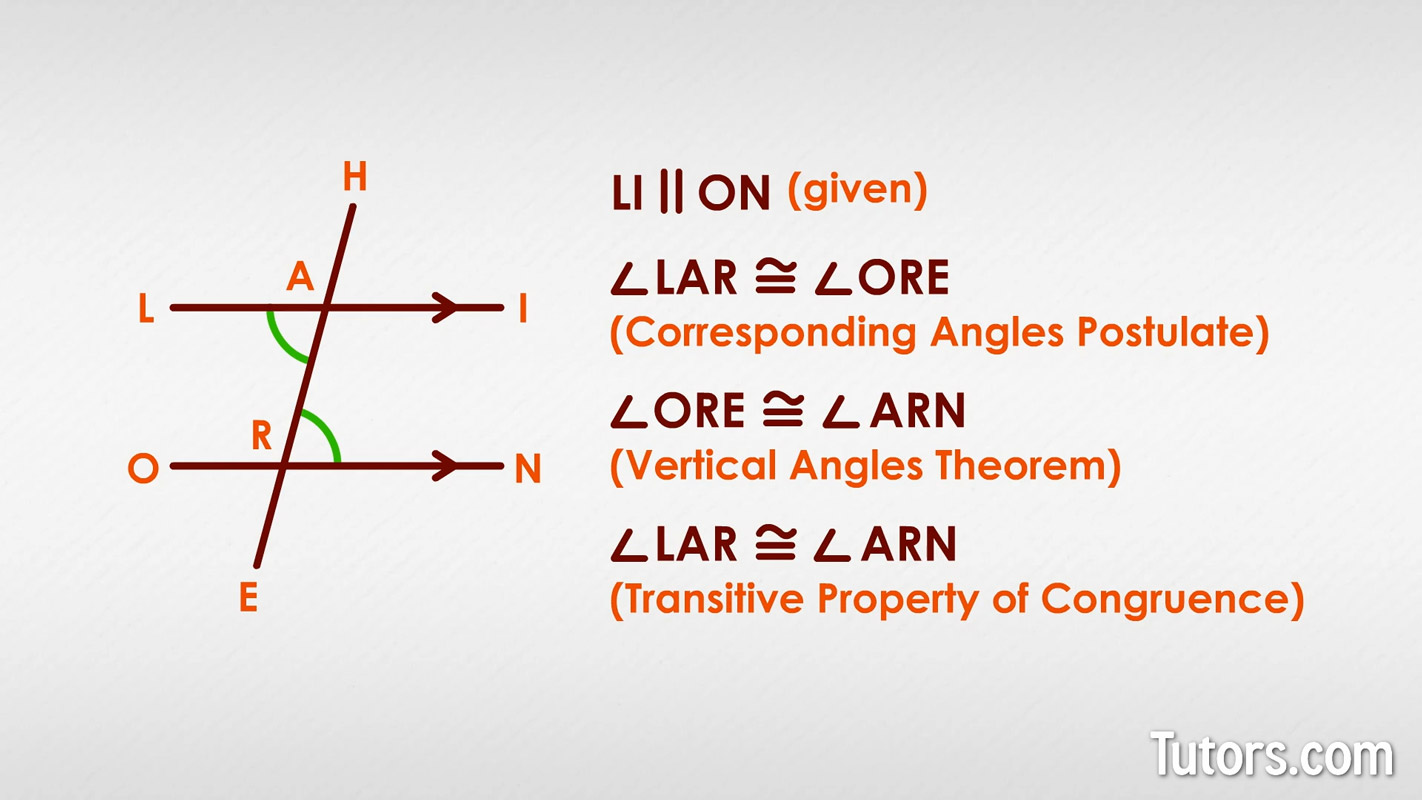
LI ∥ ON (given)
∠LAR ≅ ∠ORE (Corresponding Angles Postulate)
∠ORE ≅ ∠ARN (Vertical Angles Theorem)
∠LAR ≅ ∠ARN (Transitive Property of Congruence)
The Transitive Property of Congruence says if A is like B and B is like C, then A is like C. Since ∠LAR was congruent to ∠ORE, and ∠ORE was congruent to ∠ARN, then:
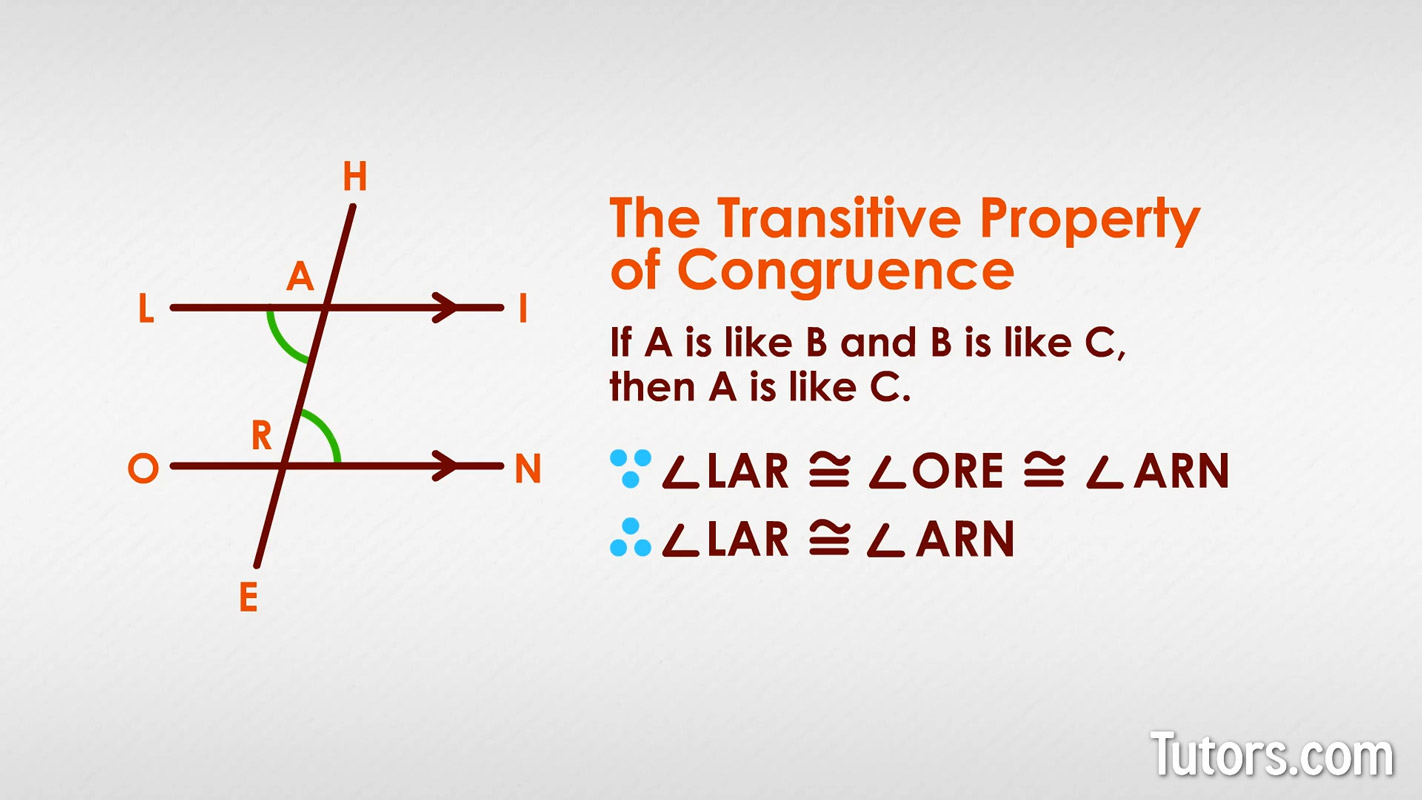
∠LAR ≅ ∠ORE ≅ ∠ARN
∠LAR ≅ ∠ARN
To prove the converse, "If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel," we work the other way around:
LI and ON with transversal HE (given)
∠LAR ≅ ∠ARN (given)
∠LAR ≅ ∠HAI (Vertical Angles Theorem)
∠HAI ≅ ∠ARN (Transitive Property of Congruence)
LI ∥ ON (Converse of Corresponding Angles Theorem)
Alternate interior angles in real life
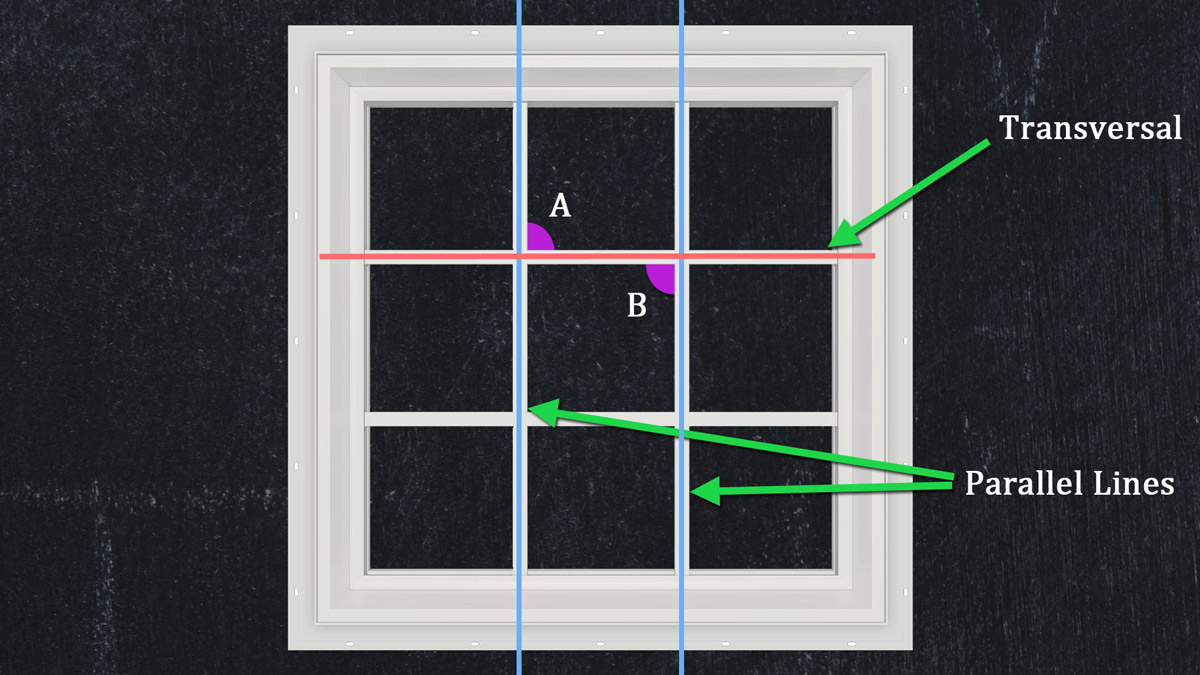
Look at a window with panes divided by muntins. Horizontal muntins transverse parallel vertical muntins. Anywhere they cross, you can find alternate interior angles.
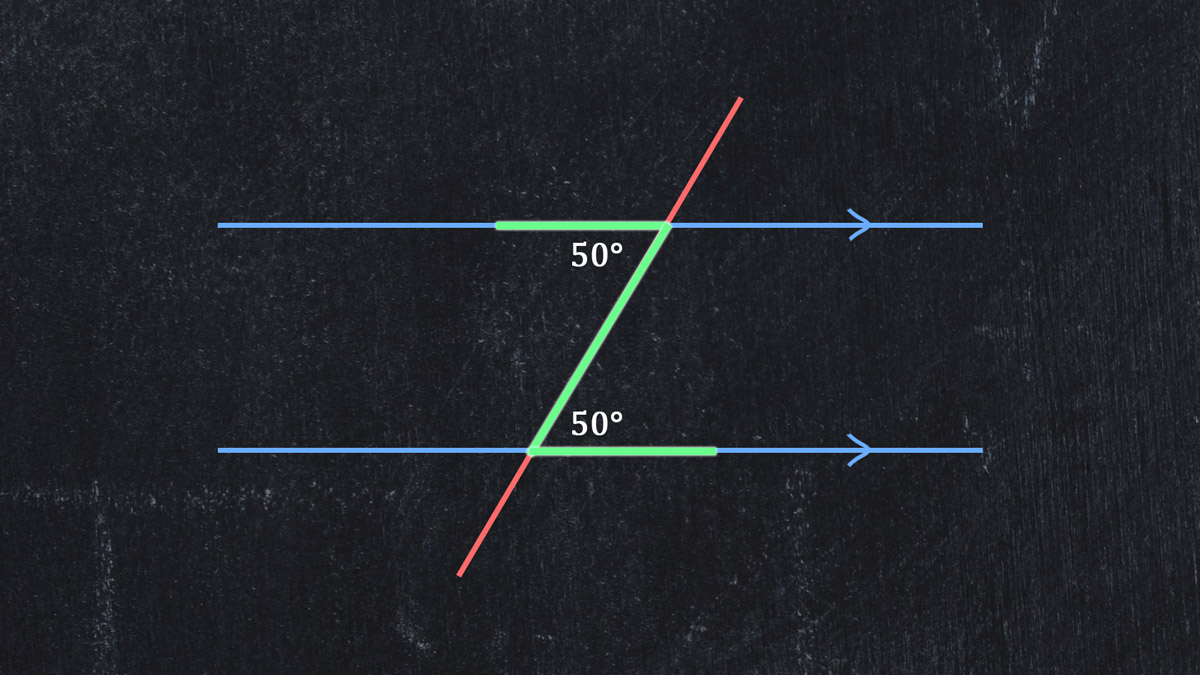
Another example of real life alternate interior angles occurs in the capital letter Z. The top and bottom horizontal lines of the letter are parallel lines, and the diagonal slash is the transversal.
If you expand all of the lines of the letter Z, you will easily see the alternate interior angles:
Lesson summary
After navigating this lesson, you are now able to define the parts of an angle (lines, rays or line segments meeting at an endpoint and forming a vertex). You can also draw, describe and identify transversal lines, straight lines, straight angles, parallel lines, and alternate interior angles.
In addition, you can now apply the Alternate Interior Angles Theorem to find angles in parallel lines crossed by a transversal. You definitely figured out the angles on this one!