Complementary Angles — Definition & Examples

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What are complementary angles?

Complementary angles are two angles that add up to exactly 90°. The two angles can be part of the same or different figures. Complementary angles do not need to be adjacent angles or oriented in the same direction. If any two angles sum to exactly 90°, then they are two complementary angles.

Any two angles, even something silly like a 1° and 89°, are complementary angles meaning they add up to exactly 90°.

If you are not using degrees, but are using radians instead, you can say the two angles add to a sum of $\frac{\pi }{2}$.

Knowing that “complementary” comes from a Latin word meaning “to complete,” you will always get complementary angles right.

Complementary angles examples

Complementary angles do not have to be part of the same figure. In the drawing below, for example, three angles are placed on a plane, but only two are complementary:

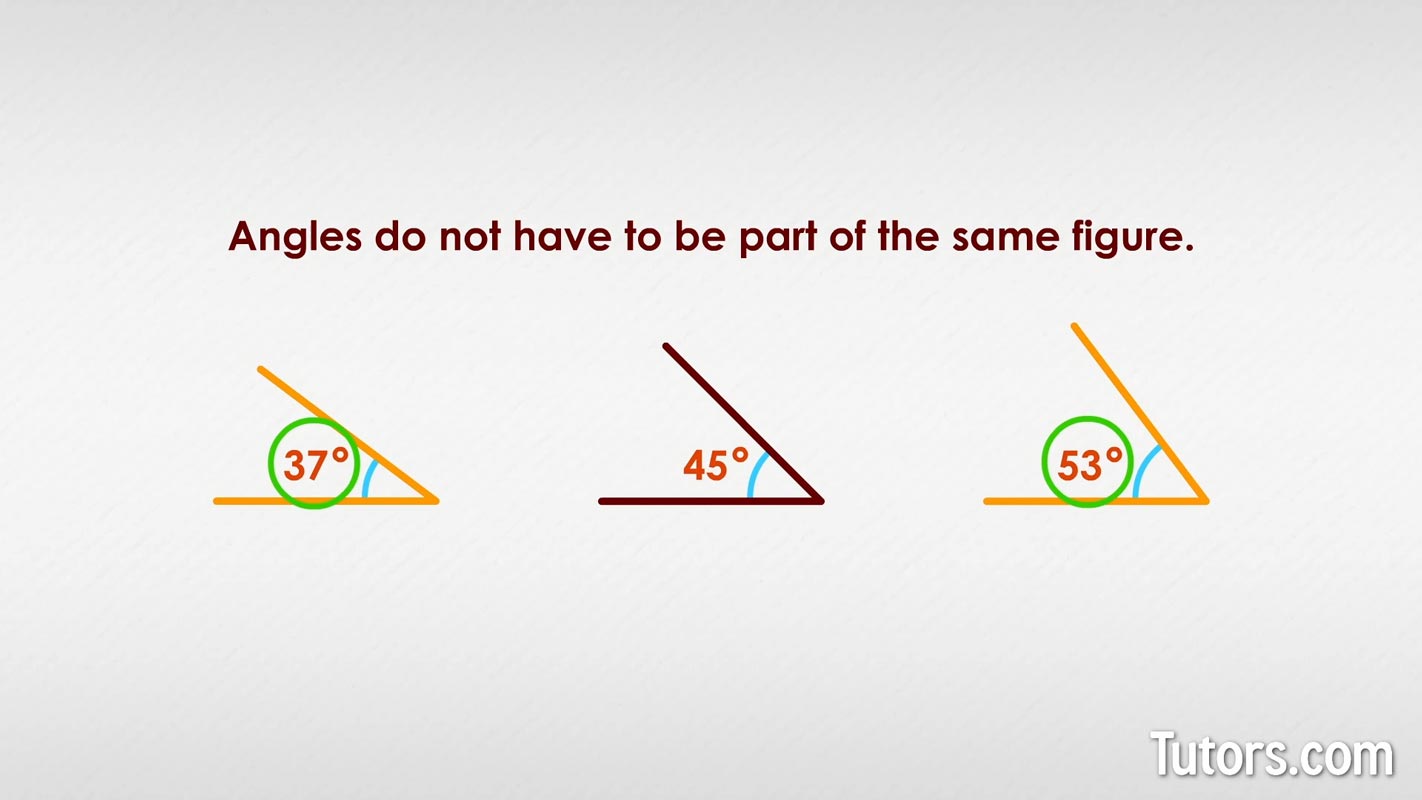
The only two numbers that sum to 90° are the first and third angles, so they are complementary angles.

Here are three more angles. Only one could be a partner for a complementary angle. Do you know which one?

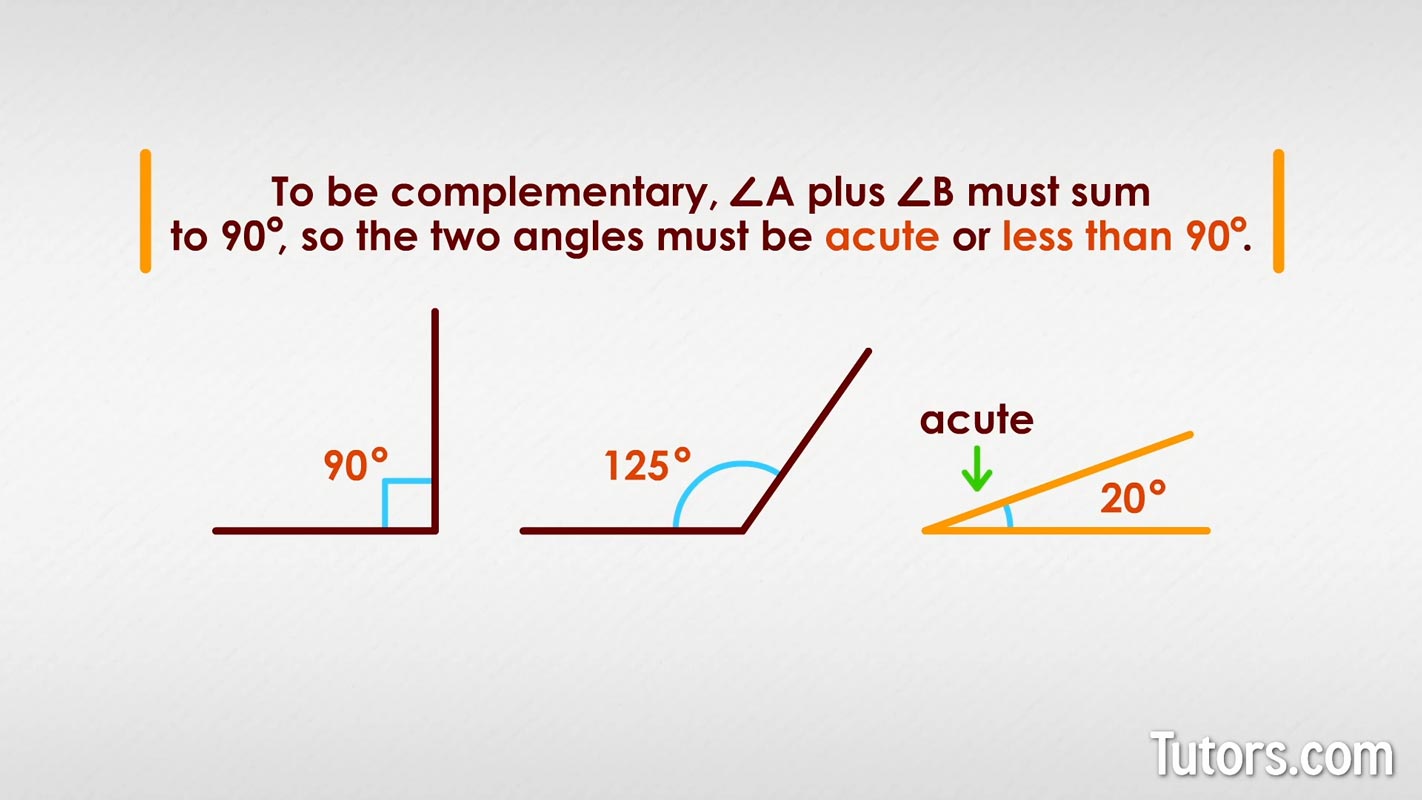
Since the sum of ∠A + ∠B must measure 90°, the two angles must be acute angles. You cannot have a right angle or obtuse angle, like the first two angles in our drawing, as one of the two complementary angles.

Sometimes angles are drawn as touching pairs. They share a side, ray, or line. In the drawing below, which angles are complementary?

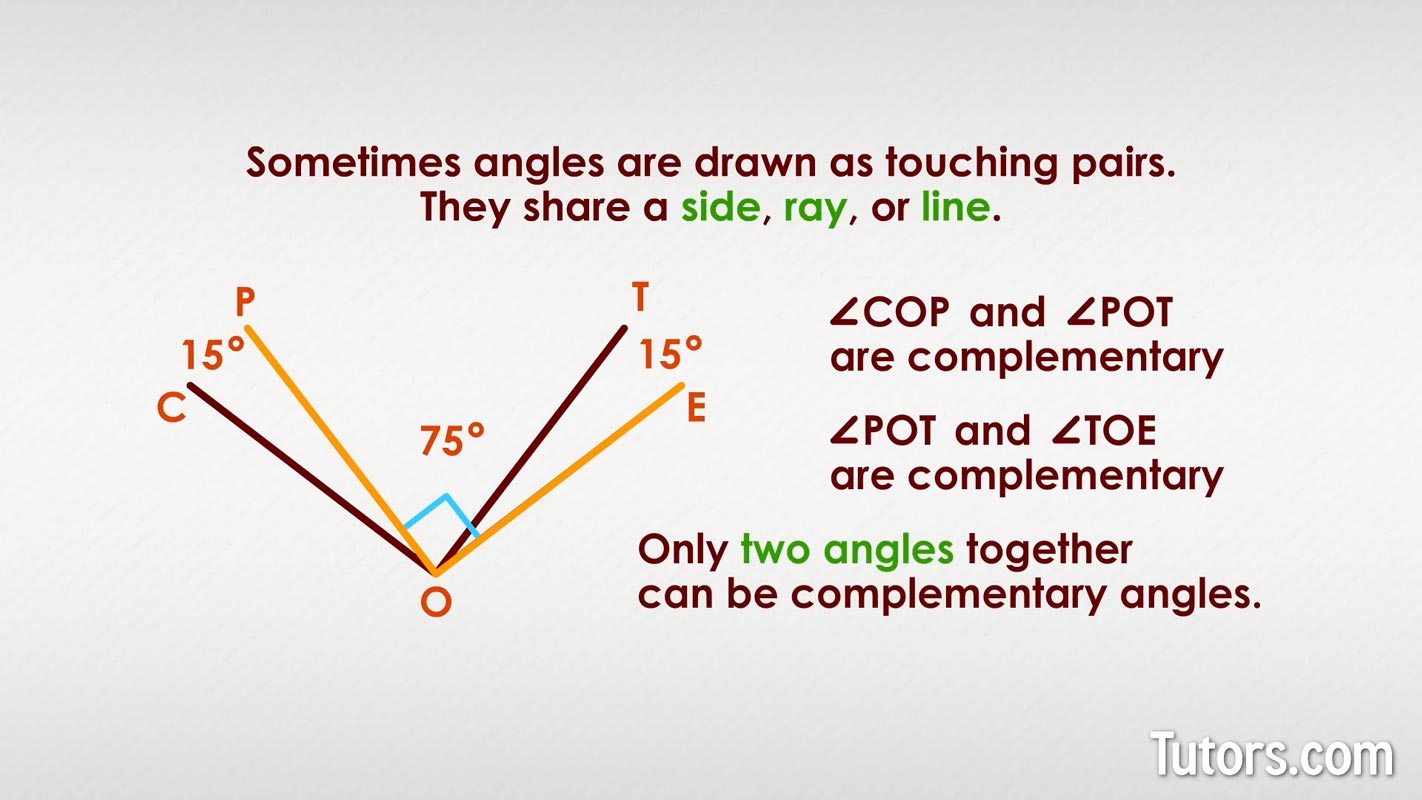
Notice that the intersecting lines of the left-hand angle and middle angle create a right angle, so ∠COP and ∠POT are complementary. The middle angle, ∠POT, and ∠TOE on the right side are complementary, too.

You cannot say all three are complementary; only two angles together can be complementary.

Complementary angles theorem

Two theorems make use of complementary angles. One states, “Complements of the same angle are congruent.” This theorem, which involves three angles, can also be stated in another way:

Since two angles must add to 90°, if one angle is given – we will call it ∠GUM – only one other measurement can be its complement.

If one angle is complementary to ∠GUM – we will call it ∠CAP – then any other angle that is also complementary to ∠GUM must be equal in measure to ∠CAP. Here is the idea visually:

We can see that ∠ELM looks as if it is the same angle as ∠CAP, which it is. Since the two angles are both complementary angles to ∠GUM, then they are congruent.

The other theorem about complementary angles states:

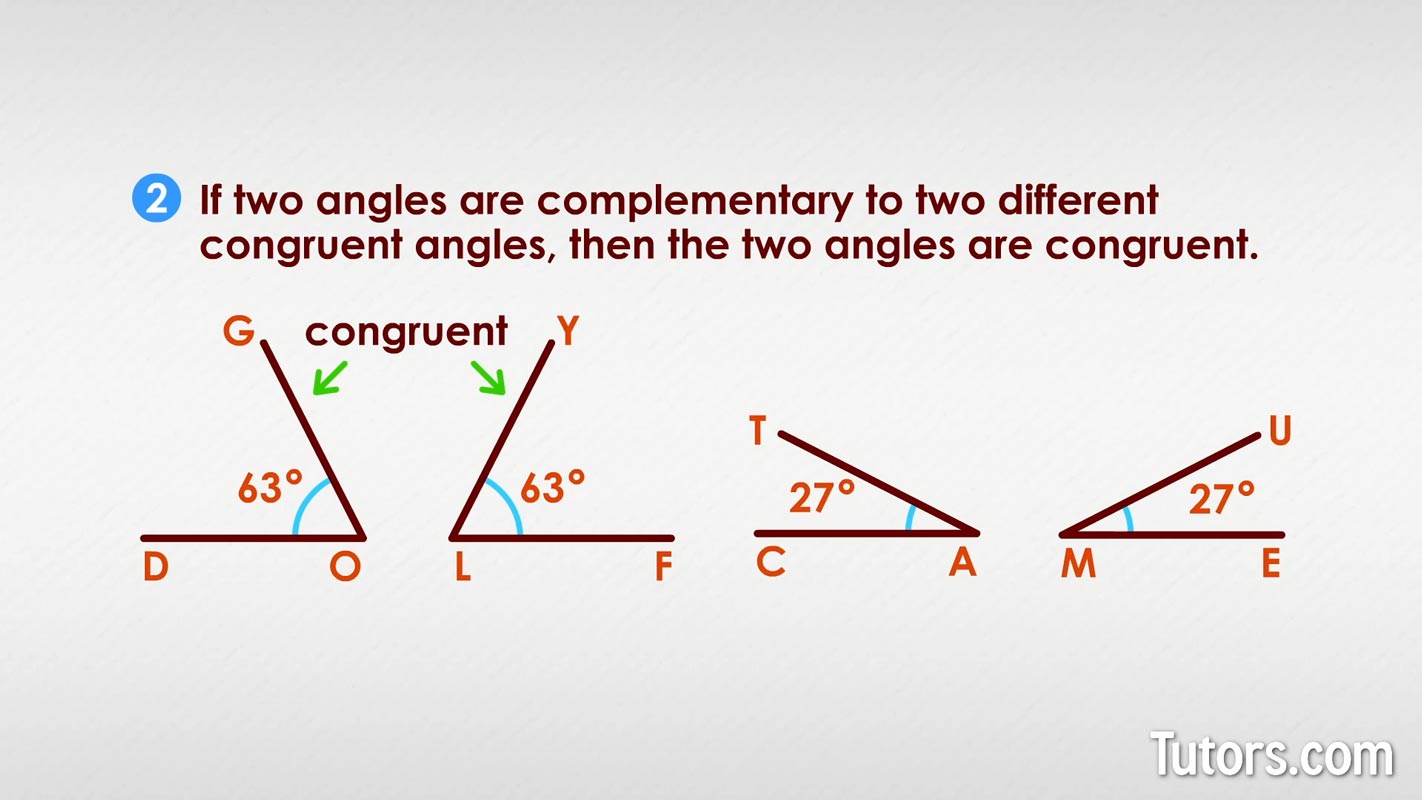
This involves four angles altogether. Say you have two congruent angles, ∠DOG and ∠FLY, each measuring 63°.

Their complementary angles are ∠CAT and ∠EMU, each measuring 27°.

You can easily see that two angles of 27° are congruent.

How to find complementary angles

If you have a given angle of 70° and told to find the complementary angle, how do you find a complementary angle?

To find the measure of an angle that is complementary to a 70° angle, you simply subtract 70° from 90°.

The missing angle measure is 20°.

An easy way to create complementary angles is with a right triangle. Simply draw a straight line beginning at the right angle vertex and through the triangle. No matter where you draw the line, you have created two complementary angles.

Complementary vs. supplementary angles

Complementary angles are two angles that sum to 90° degrees. If an angle measures 50°, then the complement of the angle measures 40°.

Supplementary angles are two angles that sum to 180° degrees. Together supplementary angles make what is called a straight angle. If you add arrows onto the ends of the straight angle, you will have a straight line.

If you have an angle that measures 100° degrees, then it's supplementary angle can only measure 80° degrees. Learn more about supplementary angles.