Angle Relationships (Types of Angles)
Types of angles
In geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. All angles have relationships to other angles and those angle relationships are what we will cover here.
Angle relationships
Beyond measuring the degrees or radians, you can also compare angles and consider their relationships to other angles. We talk of angle relationships because we are comparing position, measurement, and congruence between two or more angles.

For example, when two lines or line segments intersect, they form two pairs of vertical angles. When two parallel lines are intersected by a transversal, complex angle relationships form, such as alternating interior angles, corresponding angles, and so on.
Being able to spot angle relationships, and confidently find congruent angles when lines intersect, will make you a better, geometry student. You will solve complex problems faster when you are thoroughly familiar with all the types of angle relationships.
Congruent angles
Any two angles, no matter their orientation, that have equal measures (in radians or degrees) are congruent. They show the same "openness" between the two rays, line segments or lines that form them. So these two 35° angles are congruent, even if they are not identically presented, and are formed with different constructions:

Adjacent angles
When two lines cross each other, they form four angles. Any two angles sharing a ray, line segment or line are adjacent. In the following drawing, Line JC intersects Line OK, creating four adjacent pairs and intersecting at Point Y. Can you find them all?

Did you find ∠JYO adjacent to ∠OYC?
How about ∠OYC adjacent to ∠KYC?
You saw ∠KYC adjacent to ∠KYJ, right?
And you found ∠KYJ adjacent to ∠JYO, surely!
Vertical angles
In our same drawing above, angles that skip an angle, that is, angles that are not touching each other except at their vertex, are vertical angles. Here the word "vertical" means "relating to a vertex," not "up and down." Vertical angles are opposite angles; they share only their vertex point.

Two intersecting lines create two pairs of vertical angles. See if you can spot them in our drawing.
Did you find ∠JYO and ∠KYC made a pair? They touch only at Point Y
Did you find ∠KYJ and ∠OYC made the other pair? They also touch only at Point Y
You may wonder why adjacent angles are not also vertical angles, since they share the vertex, too. Adjacent angles share more than the vertex; they share a common side to an angle.
Corresponding angles
Anytime a transversal crosses two other lines, we get corresponding angles. The more restrictive our intersecting lines get, the more restrictive are their angle relationships. When a line crosses two parallel lines (a transversal), a whole new level of angle relationships opens up:

We can adroitly pull from this figure angles that look like each other. Angles that have the same position relative to one another in the two sets of four angles (four at the top, Line AR; four at the bottom, Line TO) are corresponding angles. When the corresponding angles are on parallel lines, they are congruent.
Our transversal and parallel lines create four pairs of corresponding angles. Can you name them all?
Did you find ∠AYD corresponding to ∠TLY?
How about ∠DYR corresponding to ∠YLO?
You found ∠RYL corresponding to ∠OLI, right?
And you did not overlook ∠AYL corresponding to ∠TLI, did you?
In all cases, since our Line AR and TO are parallel, their corresponding angles are congruent.
Exterior angles
Those same parallel lines and their transversal create exterior angles. An exterior angle among line constructions (not polygons) is one that lies outside the parallel lines. You can see two types of exterior angle relationships:
Consecutive exterior angles
When the exterior angles are on the same side of the transversal, they are consecutive exterior angles, and they are supplementary (adding to 180°). In our figure above, ∠AYD and ∠TLI are consecutive exterior angles. The only other pair of consecutive exterior angles is ∠DYR and ∠OLI.

Alternate exterior angles
Alternate exterior angles are similar to vertex angles, in that they are opposite angles (on either side of the transversal). Alternate exterior angles are on opposite sides of the transversal (that's the alternate part) and outside the parallel lines (that's the exterior part). Can you find the two pairs of alternate exterior angles in our drawing?
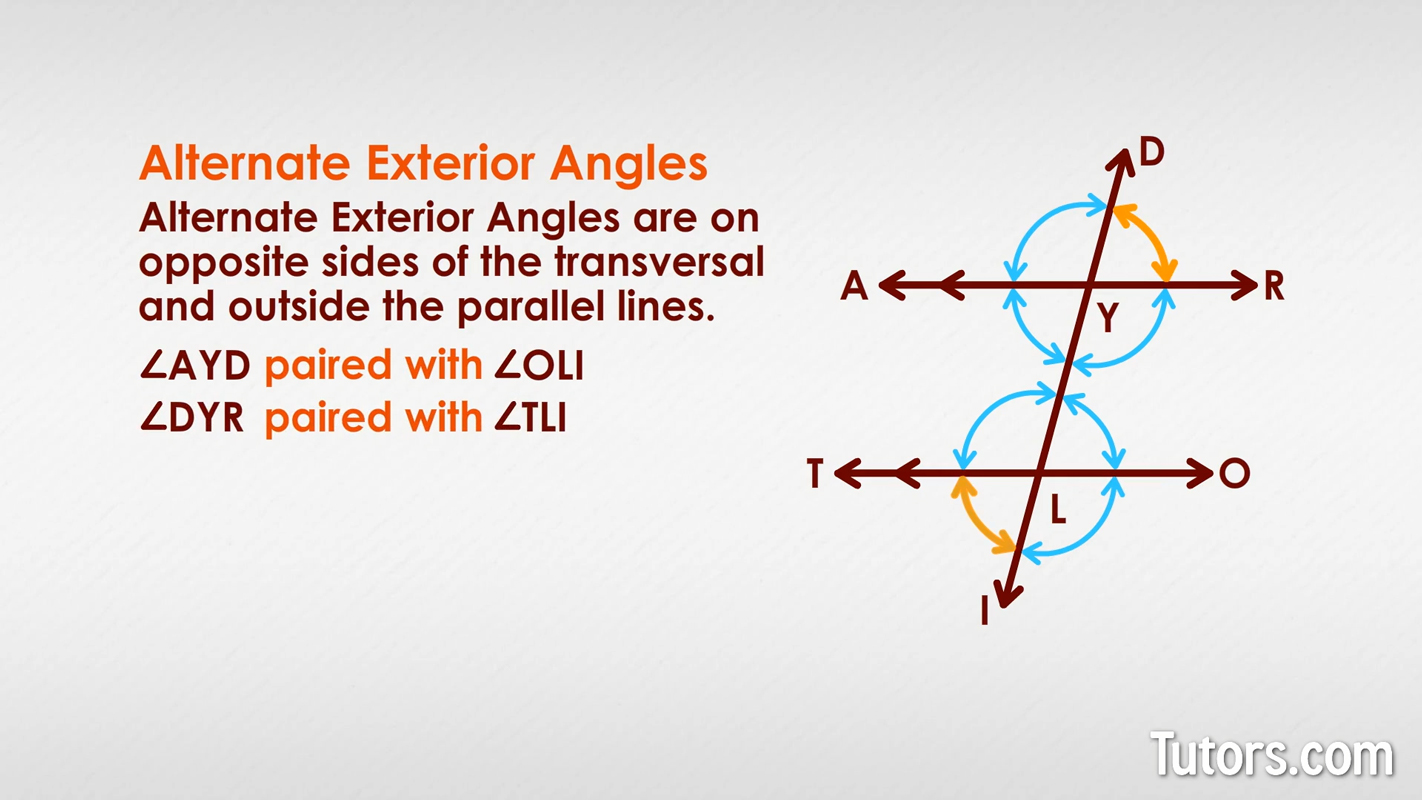
You wrote down ∠AYD and ∠OLI, and then you wrote ∠DYR paired with ∠TLI, no doubt!
Congruent alternate exterior angles are used to prove that lines are parallel, using (fittingly) the Alternate Exterior Angles Theorem.
Interior angles
Angles between the bounds of the two parallel lines are interior angles, again created by the transversal. Just as with exterior angles, we can have consecutive interior angles and alternate interior angles.
Consecutive Interior Angles
Interior angles on the same side of the transversal are consecutive interior angles. In our figure, can you find the two pairs? Did you find ∠RYL pairing off with ∠YLO? Did you see that ∠AYL paired up with ∠TLY?
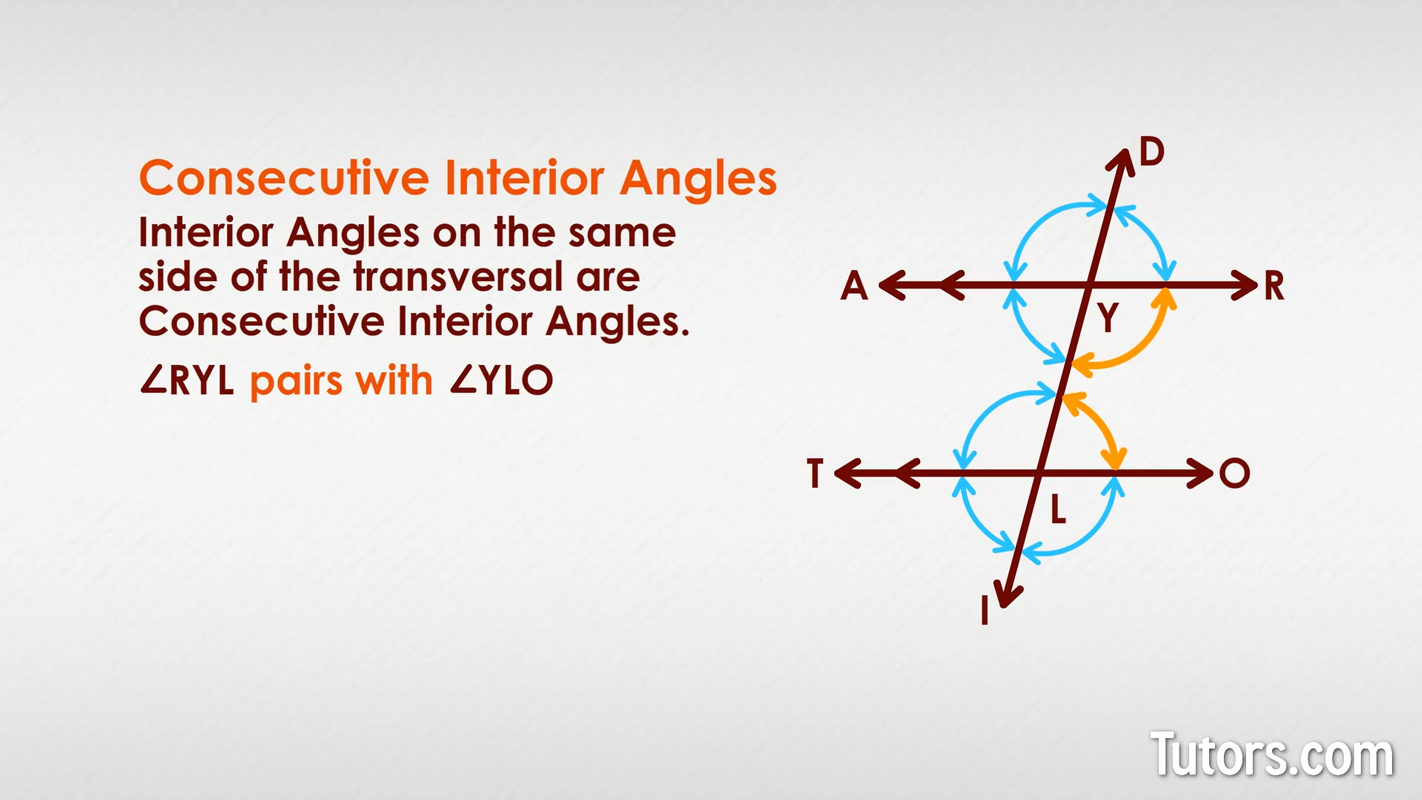
In parallel lines, consecutive interior angles are supplementary.
Alternate interior angles
When the interior angles are on opposite sides of the transversal, they are alternate interior angles. They lend themselves to the Alternate Interior Angles Theorem, which states that congruent alternate interior angles prove parallel lines (much as the Alternate Exterior Angles Theorem did).
In our figure, ∠ALY is the alternate interior angle for ∠YLO, making them congruent. And, of course, ∠RYL pairs off as the alternate interior angle of ∠TLY.
Angle relationships examples
You can use your newfound knowledge of angle relationships to solve algebraic challenges about geometric figures. When viewing any new figure, go through your list and determine three things:
Relative positions of the two questioned angles
Whether the angles are outside the parallel lines (exterior) or inside the parallel lines (interior)
Whether the two angles under investigation are on the same side of the transversal (consecutive) or opposite sides of the transversal (alternate)
Once you understand the relationship between the two angles, you can assume some basic facts, such as their congruence or that they may be supplementary.
You can use that awareness to solve seemingly difficult algebraic problems like this:
Draw parallel lines MJ and TE and the transversal AS with intersecting Point C on Line MJ and intersecting Point I on Line TE, spelling in a circular way MAJESTIC. Let ∠MCA = 123°.
Given the figure, find the value of x if ∠MCA = 4x + 3° while ∠EIS = 5x − 27°.
You see right away that these two angles, ∠MCA and ∠EIS, are exterior angles on opposite sides of the transversal. So they are alternate exterior angles, making them congruent and allowing you to set up a simple algebraic equation:
Next, we subtract 4x from both sides:
Next, we add 27° to both sides:
To find our angles, substitute 30° for x:
Though ∠EIS is supposed to be congruent, you can still check it:
Let's try a second exercise, using the same figure. If you can solve this, you will have accomplished some MAJESTIC mathematics!
What can you tell us about ∠JCI and ∠TIS?
What if we told you ∠JCI = 2y − 7° while ∠TIS = y − 8°?
Can you solve for y?
Neither angle is on the same side of the transversal, nor are they both outside the parallel lines. They are not both inside the parallel lines, either! They seem to have no relationship at all!
And yet, by deduction, you can see a relationship:
∠JCI is the consecutive interior angle partner of ∠EIC
∠EIC is the vertical angle partner of ∠TIS
This means our two problematic angles are actually supplementary, which is a great hint. Together, their two equations must add to 180°:
Now, simplify:
Need 15° to both sides:
Working back through the problem, you will find that ∠JCI = 123° and ∠TIS = 57°. Success! Practice for yourself, by constructing parallel lines with transversals and identifying all the angle relationships they create.
Remember, too, the relationships still hold when the lines cut by the transversal are not parallel; you just cannot use Theorems to make assumptions about the angles.