Congruent Angles — Definition, Symbol, & Examples

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What area congruent angles?

Congruent angles are two or more angles that are identical to one another (and to themselves). Congruent angles can be acute, obtuse, exterior, or interior angles. It does not matter what type of angle you have; if the measure of angle one is the same as angle two, they are congruent angles.

Congruent in geometry means that one figure, whether a line segment, polygon, angle, or 3D shape, is identical to another in shape and size. Corresponding angles on congruent figures are always congruent.

Congruent angles definition

The definition of congruent angles is two or more angles with equal measures in degrees or radians. Congruent angles need not face the same way or be constructed using the same figures (rays, lines, or line segments). If the two angle measurements are equal, the angles are congruent.

The easiest way to measure the number of degrees in an angle is with a protractor.

Congruent angles symbol

To talk and write about or draw angles, we need common symbols and words to describe them. We have three symbols mathematicians use:

• $\cong$ means one thing is congruent to another.

• $\angle$ means an angle.

• $\measuredangle$ is sometimes used to indicate a measured angle.

• $\unicode{xb0}$, as in $45\unicode{xb0}$, means degrees.

• rad means radians, a method of measuring angles in the metric system.

Let's look at how we can describe these two angles:

We could say that $\angle \mathrm{O}$ (angle O) and $\angle \mathrm{A}$ (angle A) are congruent, and both measure 55°. We could also say that mathematically:

Since both angles measure less than 90°, they are also acute and made using rays. The shorthand description, $\angle \mathrm{O}$ and $\angle \mathrm{A}$ identifies each angle's vertex, or point where rays meet.

Reflexive property of congruence

The Reflexive Property of Congruence tells us that any geometric figure is congruent to itself. A line segment, angle, polygon, circle, or another figure of the given size and shape is self-congruent.

Angles have a measurable degree of openness, so they have specific shapes and sizes. Therefore every angle is congruent to itself.

Congruent angles examples

Angles can be oriented in any direction on a plane and still be congruent. Just as $\angle \mathrm{DOG}$ and $\angle \mathrm{CAT}$, above, were congruent but were not “lined up” with each other, so too can congruent angles appear in any way on a page.

Here is a drawing that has several angles. Which of these angles are congruent?:

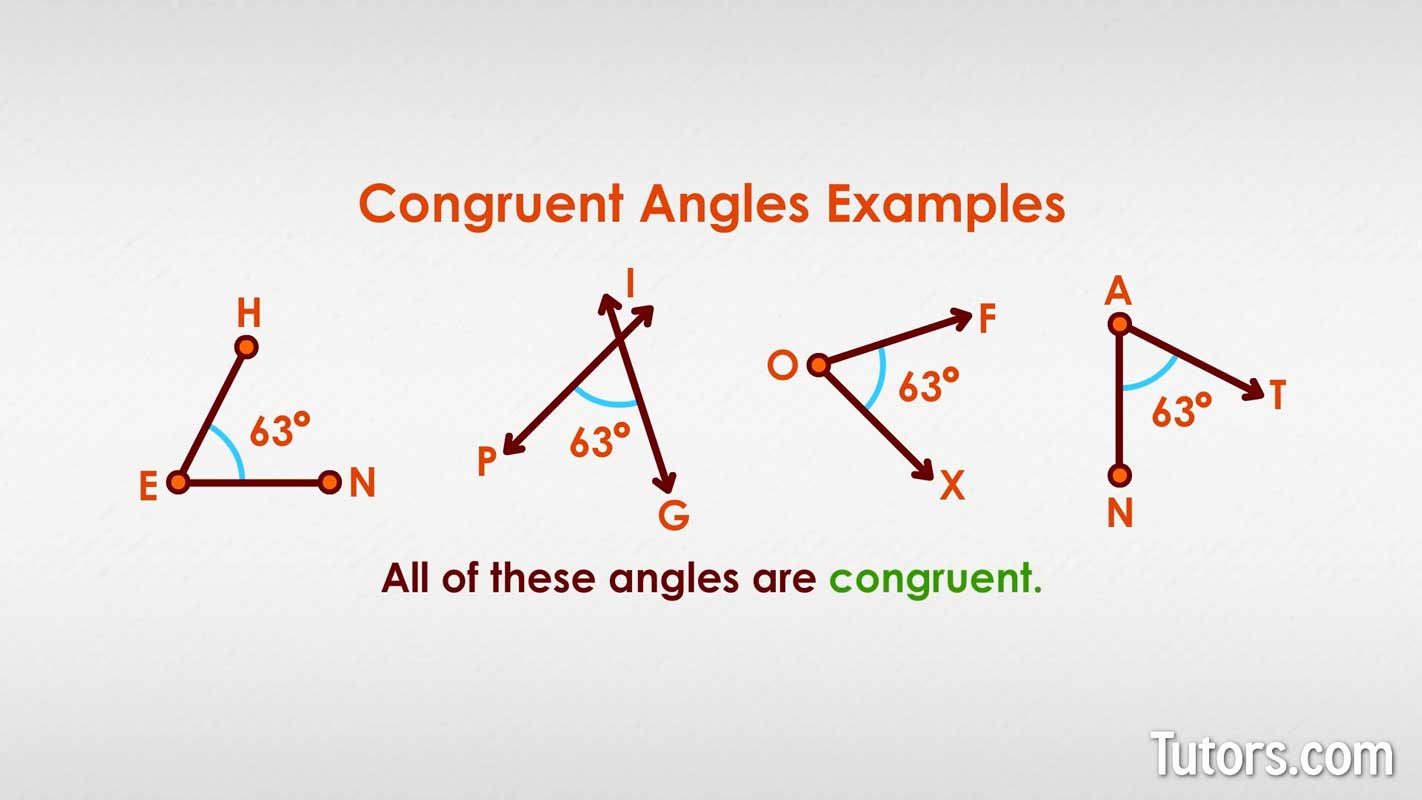
All of these angles are congruent.

The direction — the way the two angles sit on the printed page or screen — is unimportant. The way the two angles are constructed is unimportant. If the measures in degrees or radians are equal, the angles are congruent.

Drawing congruent angles

You can draw congruent angles or compare possible existing congruent angles, using a drawing compass, a straightedge, and a pencil.

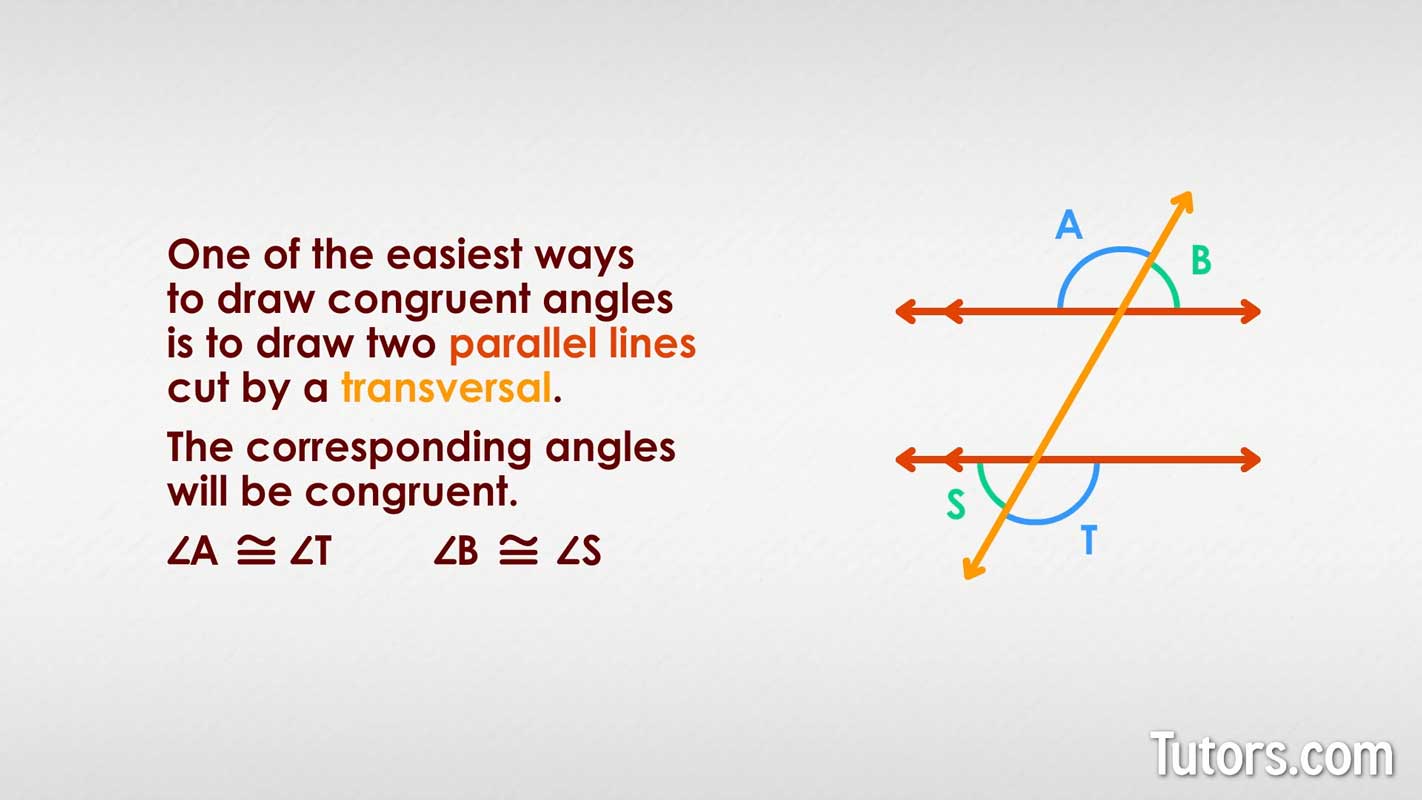
One of the easiest ways to draw congruent angles is to draw two parallel lines cut by a transversal. In your drawing, the corresponding angles will be congruent. You will have multiple pairs of angles with congruency.

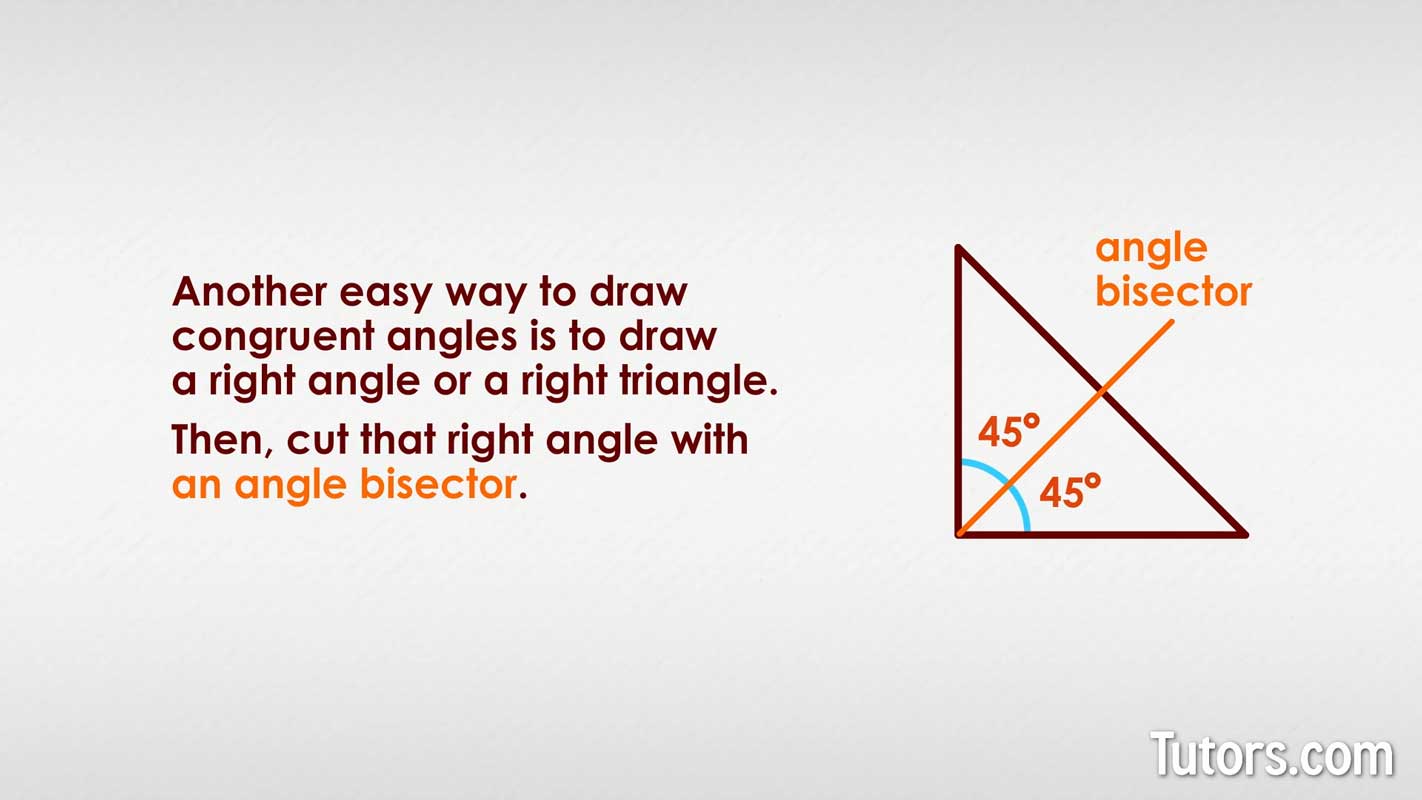
Another easy way to draw congruent angles is to draw a right angle or a right triangle. Then, cut that right angle with an angle bisector. If you bisect the angle exactly, you are left with two congruent acute angles, each measuring 45°.

But what if you have a given angle and need to draw an identical (congruent) angle next to it: Here are the steps for how to draw congruent angles:

1. Draw a ray to the right of your original angle, but some distance away. Create an endpoint for your ray and label it. We will call ours Point M.

2. Open your drawing compass so that the point on the compass can be placed on the vertex of the existing angle, but the pencil does not reach past the drawn line segments or rays of the existing angle.

3. Without changing the compass, place the point of the compass on Point M on your new drawing. Swing an arc from Point M up into the space above your new ray.

4. Move the compass point to a point on one ray of the original angle, then adjust the drawing compass so the pencil touches the other point. Here we put our compass on Point K and reach Point Y with it.

5. Without changing the compass, move the compass point to the new ray's point, here Point U, and swing the arc that intersects with your original arc.

6. Use your straightedge to connect the vertex, here Point M, with the intersection of the two arcs. You have copied the existing angle.

If you need to compare two angles that are not labeled with their degrees or radians, you can similarly use a drawing compass to locate points on both angles and measure their degree of openness.

If you do not have a protractor handy, you can use found objects to get a sense of an angle's measurement. The square edge of a sheet of paper is 90°. If you fold that corner over so the two sides exactly line up, you have a 45° angle.

The position or orientation of two angles has nothing to do with their congruence. Angles can be congruent while facing in two different directions.

Congruent angles word problems

1. Suppose you are told that two angles of two different triangles are congruent. Does that mean the triangles must be congruent?

2. One angle measures 91° and is constructed of two rays. Another angle measures 91° but is constructed of two line segments. Are the two angles congruent?

3. Two angles are each 47°, but one is made from a line and ray, and the other is made from a line segment and a line. Are the two angles congruent?

4. An angle measures 1.8 rad. Is the angle congruent to anything?

Just as any angle is true to itself by being congruent, be true to yourself by doing the work first before checking out the answers!

1. Two angles of two different triangles can be congruent, but that does not mean you have congruent triangles; they could be different sizes, and their other angles could have different measures.

2. The two angles, one measuring 91° and constructed of two rays and the other, also measuring 91° but constructed of two line segments, are congruent. Only the angle matters.

3. Two angles, each measuring 47°, are congruent, no matter how they are constructed.

4. An angle measuring 1.8 rad is congruent to itself.