Vertical Angles — Definition, Theorem, and Examples
Vertical angles definition
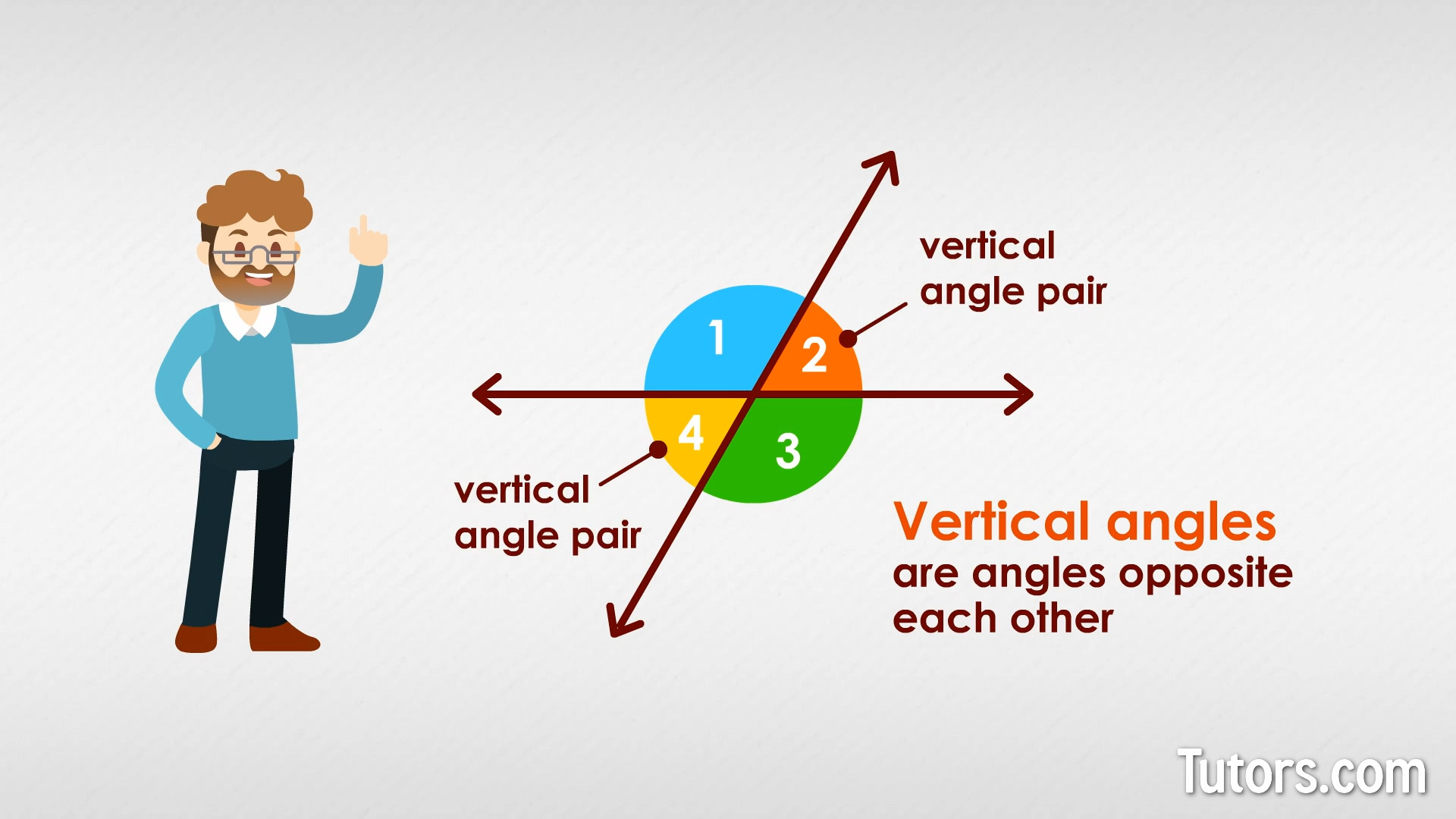
When two lines intersect in geometry, they form four angles. Vertical angles are angles opposite each other.
Any two intersecting lines form two pairs of vertical angles, like this:
Just a quick look at the drawing brings to mind several nagging questions:
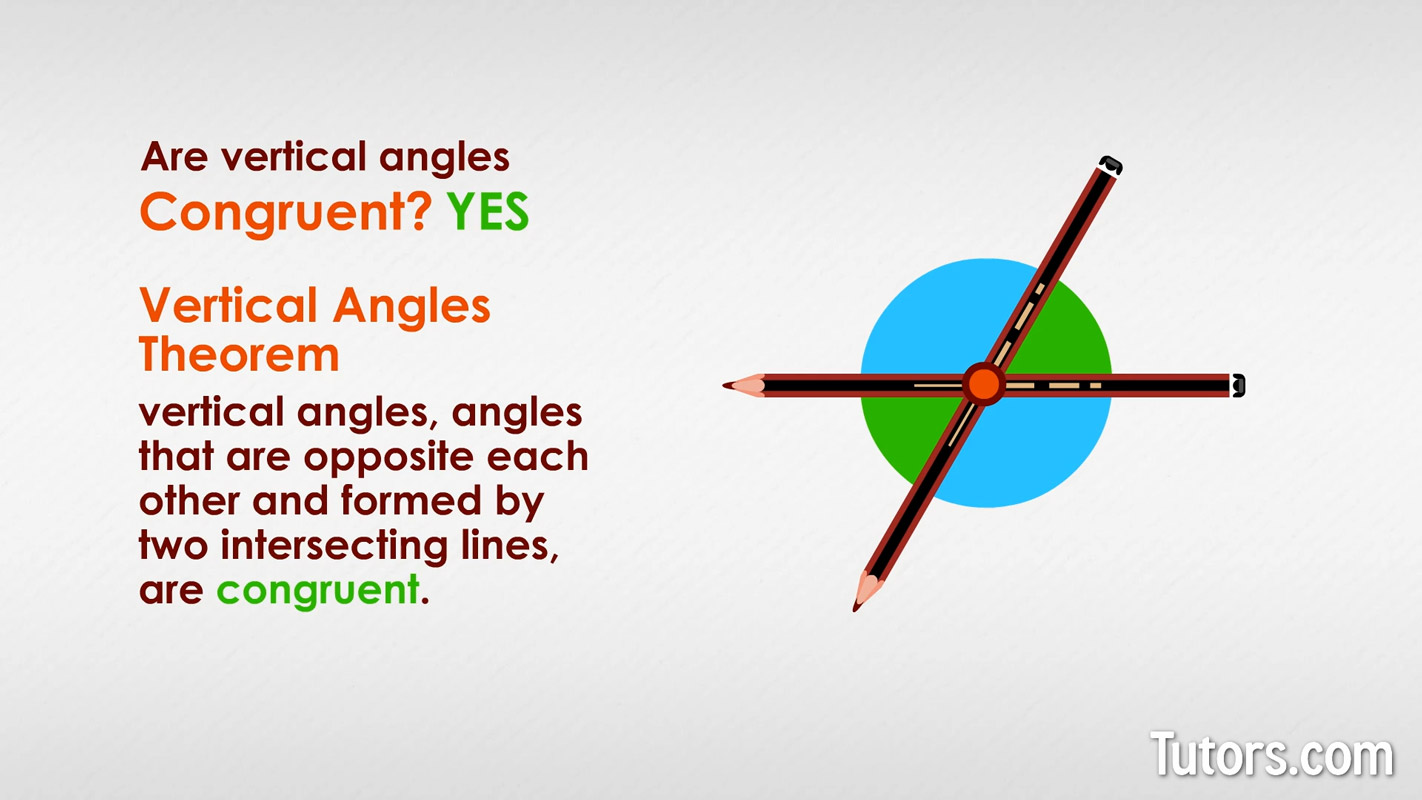
Are vertical angles congruent?
Are vertical angles adjacent?
Are vertical angles supplementary?
Are vertical angles complementary?
If you study any pair of opposite angles you will see they share a common point at their vertices, their corners. That makes them vertical angles. You will also notice that, large or small, they seem to be mirror images of each other. They are; they are the same angle, reflected across the vertex.
The word "vertical" usually means "up and down," but with vertical angles, it means "related to a vertex," or corner.
Vertical angles theorem
Vertical Angles Theorem states that vertical angles, angles that are opposite each other and formed by two intersecting straight lines, are congruent. Vertical angles are always congruent angles, so when someone asks the following question, you already know the answer.
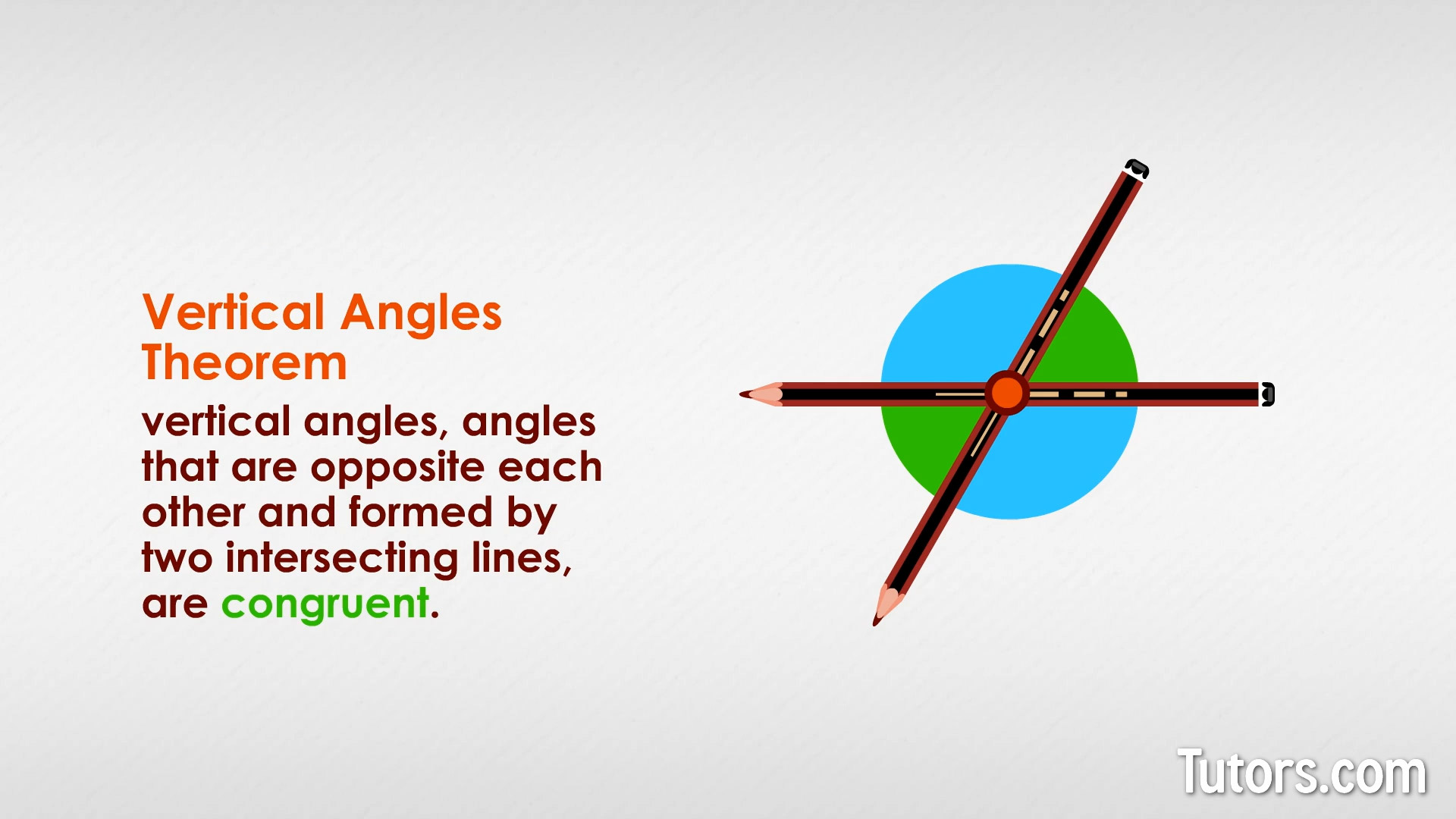
Are vertical angles congruent?
Yes, according to vertical angle theorem, no matter how two intersecting lines cross, vertical angles will always be congruent, or equal to each other. This is enshrined in mathematics in the Vertical Angles Theorem.
Are vertical angles adjacent?
Vertical angles cannot, by definition, be adjacent (next to each other). Another pair of vertical angles interrupts since opposite angles are vertical. Adjacent angles take one angle from one pair of vertical angles and another angle from the other pair of vertical angles.
Are vertical angles supplementary?
Supplementary angles add to 180°, and only one configuration of intersecting lines will yield supplementary, vertical angles; when the intersecting lines are perpendicular.
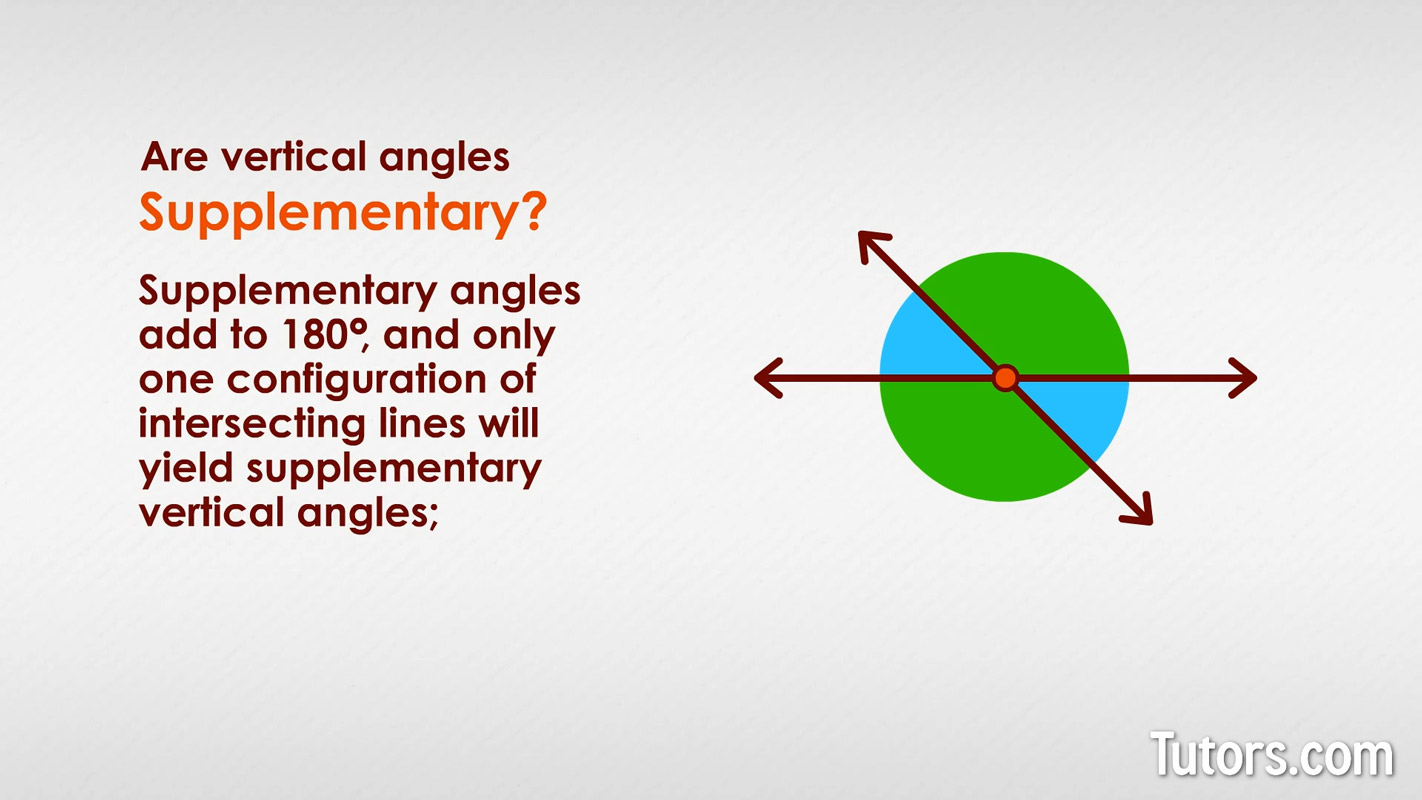
This becomes obvious when you realize the opposite, congruent vertical angles, call them aa must solve this simple algebra equation:
You have a 1-in-90 chance of randomly getting supplementary, vertical angles from randomly tossing two line segments out so that they intersect.
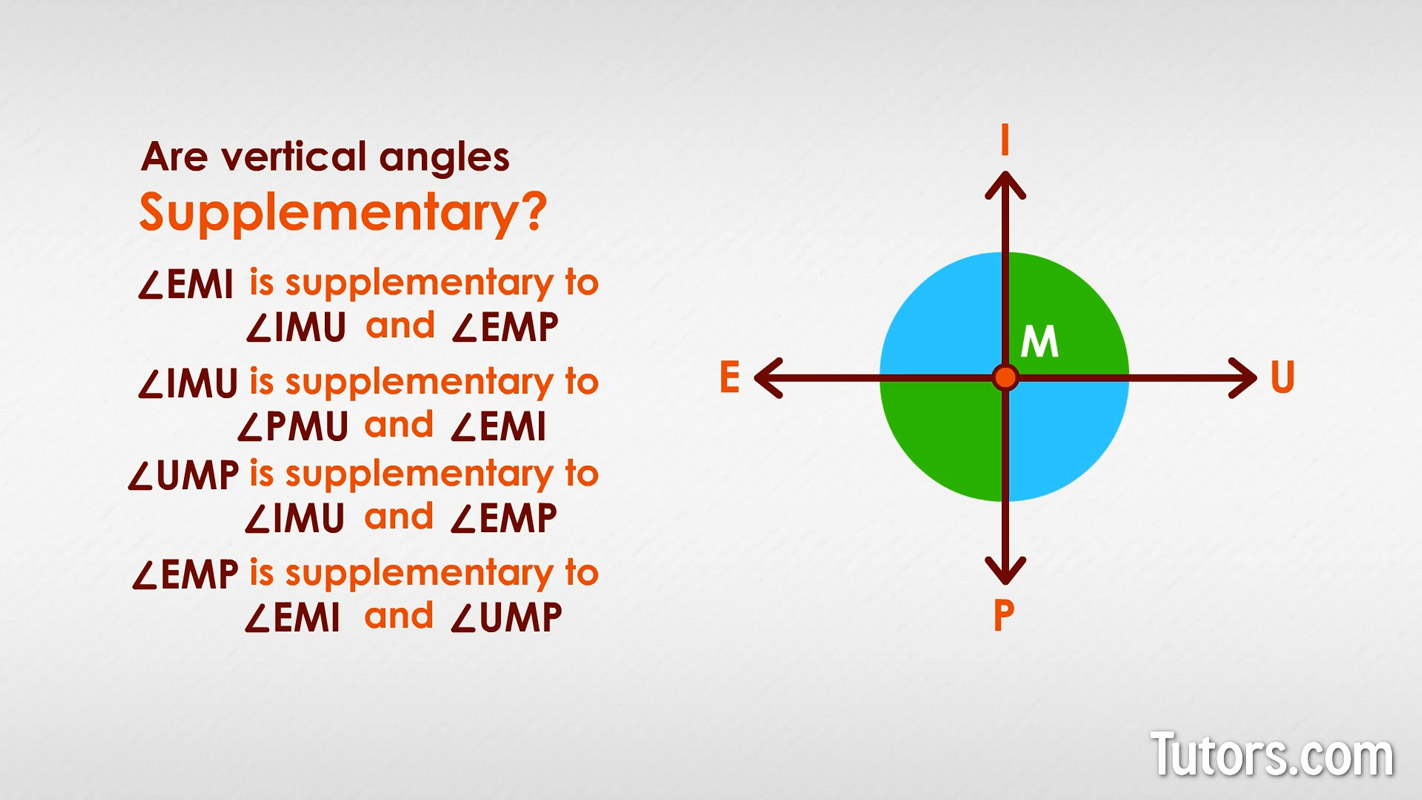
While vertical angles are not always supplementary, adjacent angles are always supplementary. Take any two adjacent angles from among the four angles created by two intersecting lines. Those two adjacent angles will always add to 180°. We can see this if we start at the top left and work our way clockwise around the figure:
∠EMI is supplementary to ∠IMU and ∠EMP
∠IMU is supplementary to ∠PMU and ∠EMI
∠UMP is supplementary to ∠IMU and ∠EMP
∠EMP is supplementary to ∠EMI and ∠UMP
Are vertical angles complementary?
If vertical angles are not always supplementary, are they at least complementary angles, that is, adding to 90°?
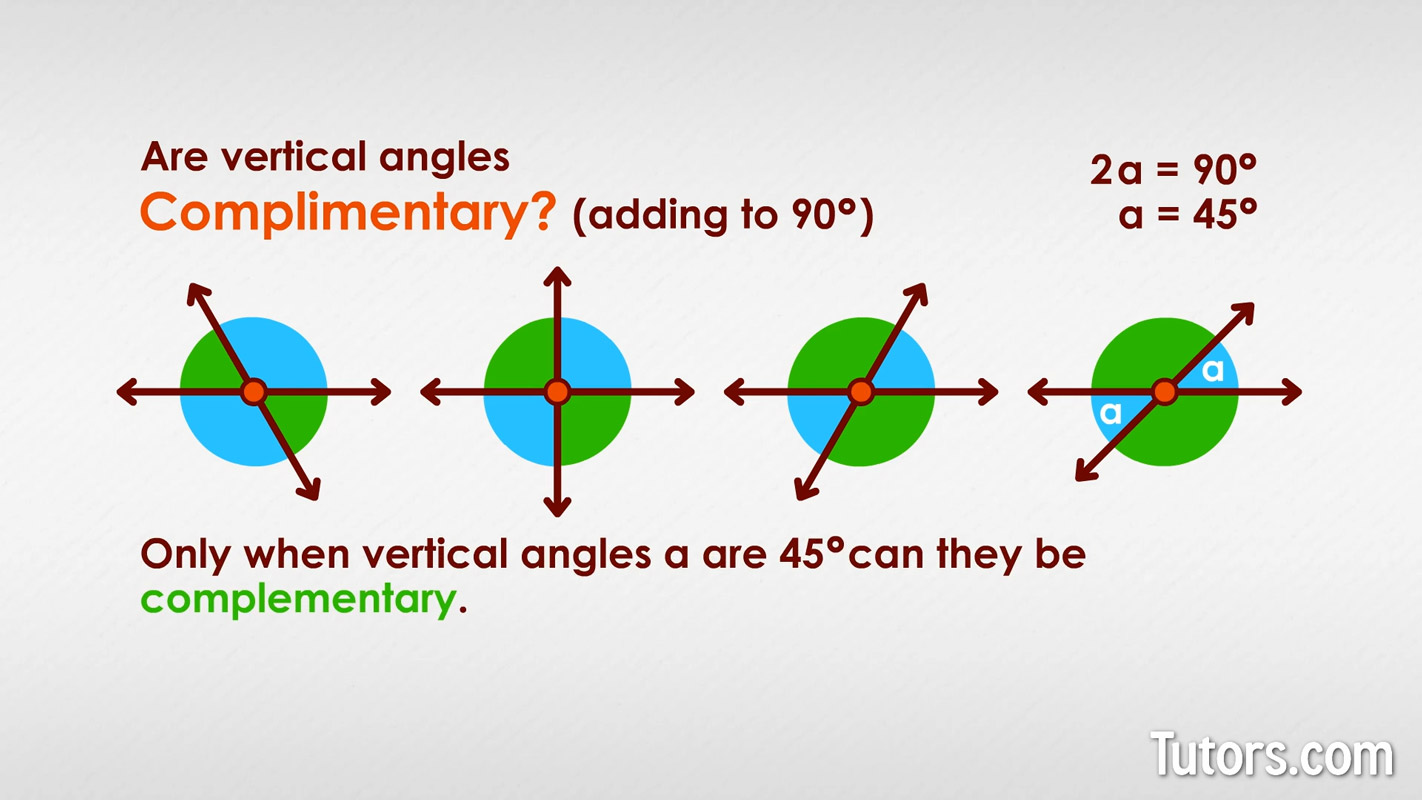
Again, we can use algebra to support what is evident in the drawings for vertical angle a:
Only when vertical angles, aa, are 45° can they be complementary. Acute vertical angles could be complementary; you have a 1-in-45 chance of that.
Complementary angles example
Complementary angles add to 90°. Complementary angles need not be connected with a common vertex or point, or line. They can be adjacent or vertical in intersecting lines. They could be in two different polygons, so long as the sum of their angles is exactly 90°. Complementary angles are each acute angles.
In most cases, you can only find the measure of one complementary angle if you know the measure of its complement. If you are told a triangle has ∠T complementary to ∠P in an irregular pentagon, you cannot know anything about the two angles other than they are both acute.
If, though, we say ∠P in the pentagon measures 57°, then we immediately know the missing ∠T, angle measures 33°:

Vertical angles quiz
A pair of vertical angles are formed when two lines intersect. Vertical angles are opposite to each other and share a vertex. Let's review what else we have learned about vertical angles:
Can vertical angles be congruent?
Can vertical angles be supplementary?
When will vertical angles be complementary?
For #1, We hope you said vertical angles are always congruent!
For #2, the answer is that vertical angles are only supplementary when lines are perpendicular.
For #3, vertical angles will be complementary only when they each measure 45°.