What Are Adjacent Angles? - Definition & Examples
Adjacent angles definition
Adjacent angles are a pair of angles that share a common side and vertex.
Three features make adjacent angles easy to pick out:
Adjacent angles exist as pairs
They share a common vertex
They share a common side

If the two angles only share a common vertex, then they are vertical angles. Vertical angles are a pair of opposite angles made by two intersecting lines.
What is a common vertex?
A common vertex is a vertex that is shared by two angles. A vertex is the point at the intersection of any two linear constructions.
Line
Line segment
Ray
You can mix and match these to create vertices (the plural of vertex) in many ways:

You see vertices in the corners of polygons, as central angles in circles, and when linear constructions, like parallel lines and transversals, cross.
What is a common side in geometry?
A common side is one line, ray, or line segment used to create two angles sharing the same vertex. Both angles use the common side and one other side.

Adjacent angles are always pairs and never overlap.
Let's see how one vertex of a square can demonstrate adjacent angles.
Here we have a simple square formed by four sides creating four vertices: ∠W, ∠H, ∠I, and ∠Z.

If we connect Point W with Point I, we construct diagonal WI. This creates two additional angles at Point W:
∠ZWI
∠HWI
Notice both those angles share a common vertex at Point W, and a common side, line segment WI. Angles ∠ZWI and ∠HWI are adjacent angles.
Linear pairs
When a pair of adjacent angles create a straight line or straight angle, they are a linear pair. The sum of their angles is 180° or π radians.
Angles that sum to 180° are called supplementary angles. Here is a linear pair. See if you can identify the common side and common vertex:
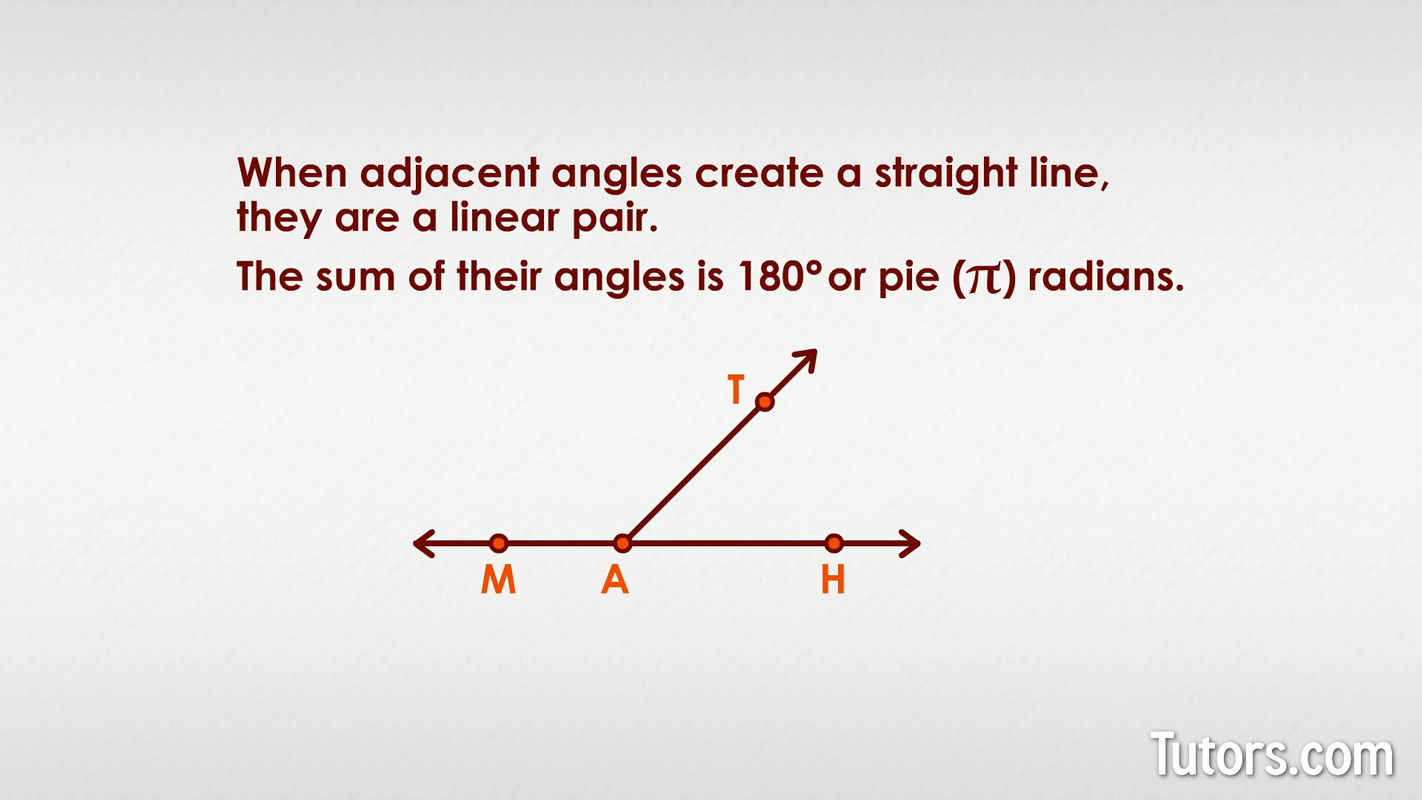
Ray AT is the common ray of both angles. Did you identify ∠A as the common vertex?
Parallel lines and transversals
Here are parallel lines CP and MN cut by transversal IK. Where the transversal cuts across them, we have points H and U:
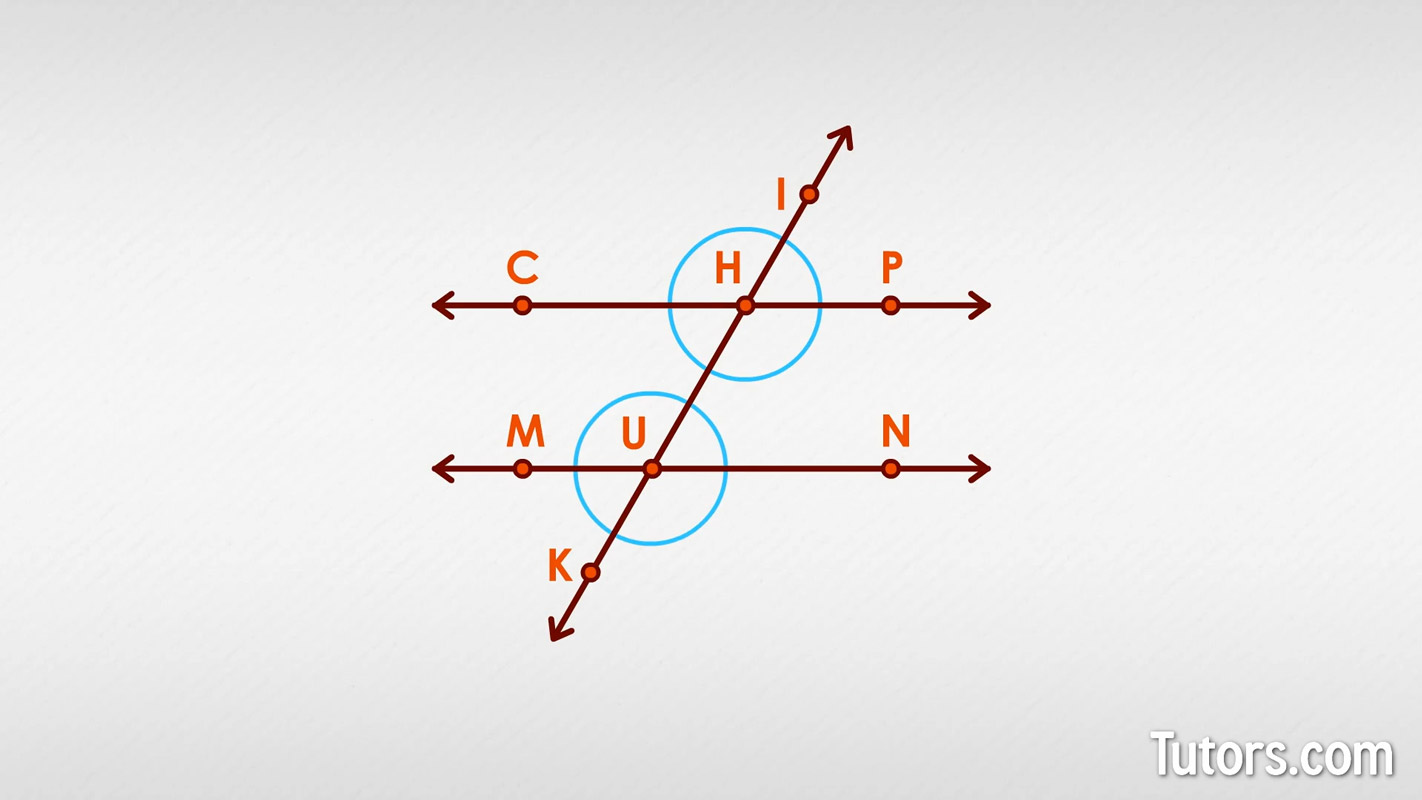
Not only does this construction form eight pairs of angles (adjacent angles), but all those pairs are also linear pairs! Which angles are adjacent angles?
∠CHI and ∠PHI
∠CHI and ∠CHU
∠PHI and ∠PHU
∠CHU and ∠PHU
∠MUK and ∠NUK
∠MUH and ∠NUH
∠MUH and ∠MUK
∠NUH and ∠NUK
These are all examples of adjacent angles. Adjacent angles can help prove that lines are parallel.
Adjacent angles example
May 12 is the birthday of Maryam Mirzakhani, a famous mathematician who studied a special kind of geometry called hyperbolic geometry. To celebrate her work, your math club bakes a birthday cake and puts you in charge of slicing it into eighths:

Are all the angles of Maryam's cake adjacent angles?
Well, no. ∠IMY is adjacent to both ∠RMI and ∠YMN, but notice that ∠RMI is not adjacent to ∠YMN, even if both angles share vertex M.
Angle relationships like adjacent angles must share both a common vertex (Point M) and a common side. ∠RMI shares no common side with ∠YMN.
Can you find any linear pairs in Maryam's cake? We hope so! For each diameter of Maryam's cake, three linear pairs exist!
To see that, we can take just one line segment, YA, as an example. You can create the straight line YA with these three linear pairs:
∠YMI and ∠IMA
∠YMR and ∠RMA
∠YMZ and ∠ZMA
Adjacent angles are two angles sharing a common vertex and a common side. They appear in many places but are prominent in parallel lines cut by transversals.