Angles, Parallel Lines, & Transversals
What makes lines parallel?
Two lines are parallel if they never meet and are always the same distance apart. Both lines must be coplanar (in the same plane). To use geometric shorthand, we write the symbol for parallel lines as two tiny parallel lines, like this: ∥∥. For example, to say line JIJI is parallel to line NXNX, we write:
How can you prove two lines are actually parallel? As with all things in geometry, wiser, older geometricians have trod this ground before you and have shown the way. By using a transversal, we create eight angles which will help us.

What are parallel lines in real life?
If you have ever stood on unused railroad tracks and wondered why they seem to meet at a point far away, you have experienced parallel lines (and perspective!). If the two rails met, the train could not move forward. Other parallel lines are all around you:
Street markings
Crosswalks
Bookshelves
Notebook paper
Parallel lines cut by a transversal
A line cutting across another line is a transversal. When cutting across parallel lines, the transversal creates eight angles. Create a transversal using any existing pair of parallel lines, by using a straightedge to draw a transversal across the two lines, like this:
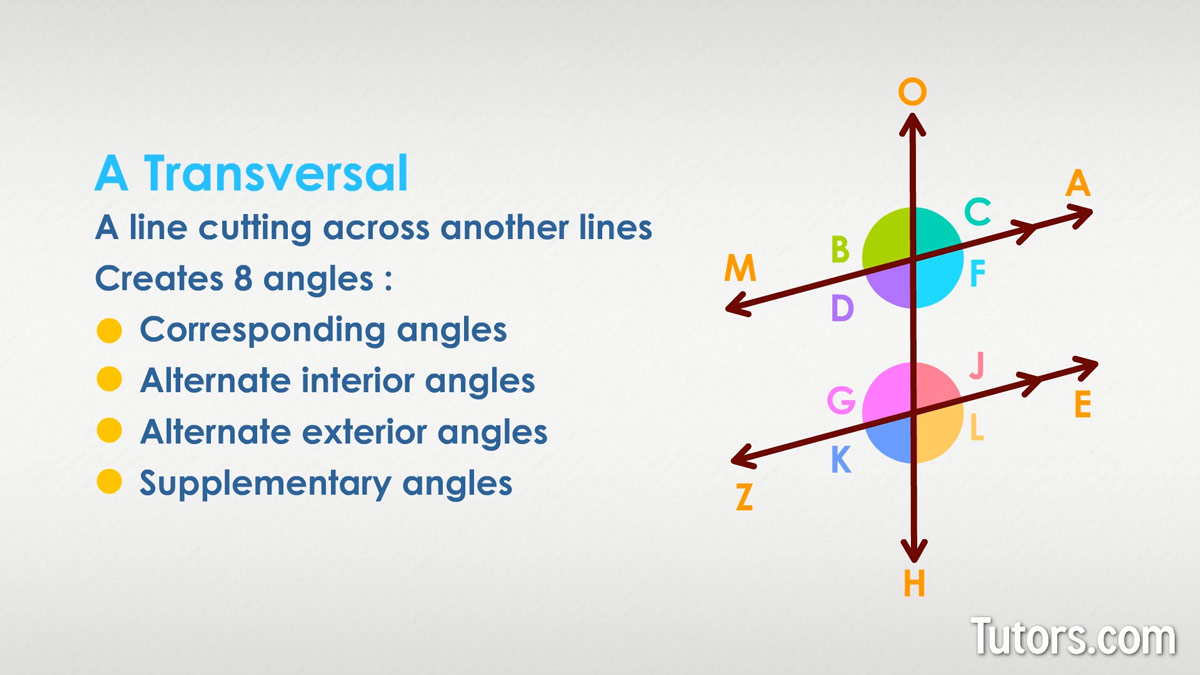
Proving lines are parallel
Those eight angles can be sorted out into pairs. Let's label the angles, using letters we have not used already:
Angles in parallel lines
These eight angles in parallel lines are:
Corresponding angles
Alternate interior angles
Alternate exterior angles
Supplementary angles
Every one of these has a postulate or theorem that can be used to prove the two lines MA and ZE are parallel. Let's go over each of them.
Corresponding angles
The corresponding angles postulate states that parallel lines cut by a transversal yield congruent corresponding angles. We want the converse of that, or the same idea the other way around:
To know if we have two corresponding angles that are congruent, we need to know what corresponding angles are. In our drawing, transversal OH sliced through lines MA and ZE, leaving behind eight angles. Each slicing created an intersection.
If one angle at one intersection is the same as another angle in the same position in the other intersection, then the two lines must be parallel. Two angles are corresponding if they are in matching positions in both intersections.
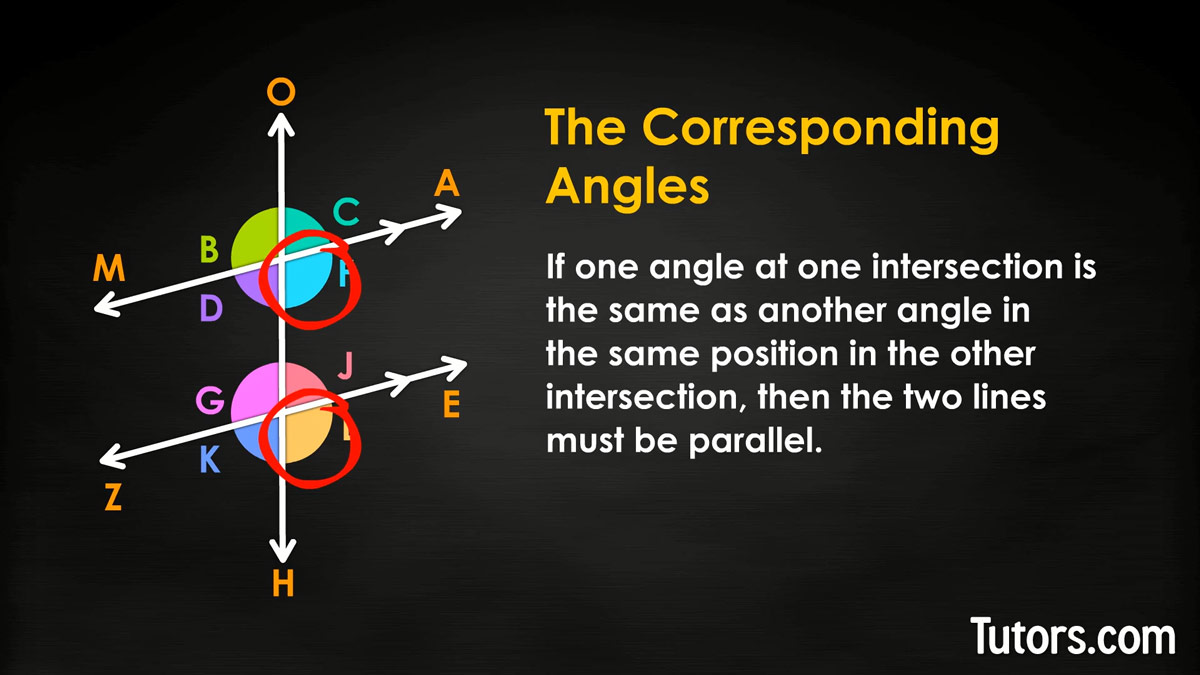
In our drawing, the corresponding angles are:
∠B and ∠G
∠C and ∠J
∠F and ∠L
∠D and ∠K
Alternate angles
Alternate angles as a group subdivide into alternate interior angles and alternate exterior angles. Exterior angles lie outside the open space between the two lines suspected to be parallel. Interior angles lie within that open space between the two questioned lines.
In our drawing, ∠B, ∠C, ∠K and ∠L are exterior angles. Can you identify the four interior angles?
Did you say ∠D, ∠F, ∠G and ∠J?
Alternate angles appear on either side of the transversal. They cannot by definition be on the same side of the transversal. In our drawing, ∠B is an alternate exterior angle with ∠L. ∠D is an alternate interior angle with ∠J. Can you find another pair of alternate exterior angles and another pair of alternate interior angles?
Here are both pairs of alternate exterior angles:
∠B and ∠L
∠C and ∠K
Here are both pairs of alternate interior angles:
∠D and ∠J
∠F and ∠G
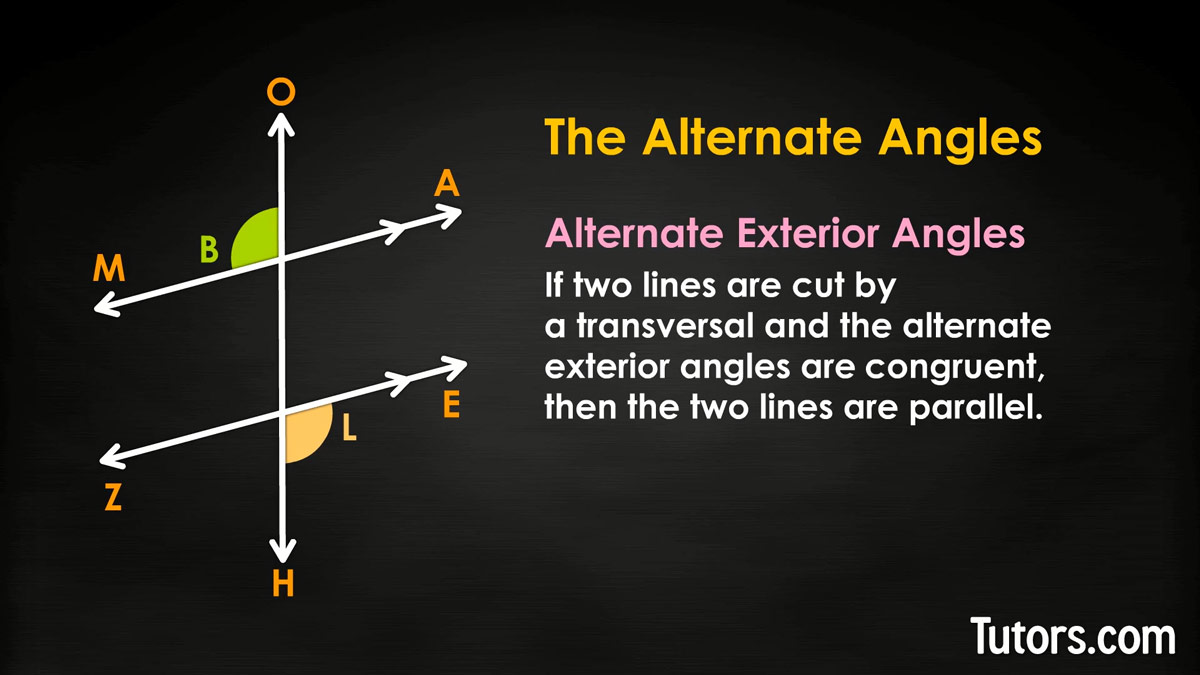
Alternate exterior angles
If just one of our two pairs of alternate exterior angles are equal, then the two lines are parallel, because of the alternate exterior angle converse theorem, which says:
Angles can be equal or congruent; you can replace the word "equal" in both theorems with "congruent" without affecting the theorem.
So if ∠B and ∠L are equal (or congruent), the lines are parallel. You could also only check ∠C and ∠K; if they are congruent, the lines are parallel. You need only check one pair!
Alternate interior angles
Just like the exterior angles, the four interior angles have a theorem and converse of the theorem. We are interested in the alternate interior angle converse theorem:
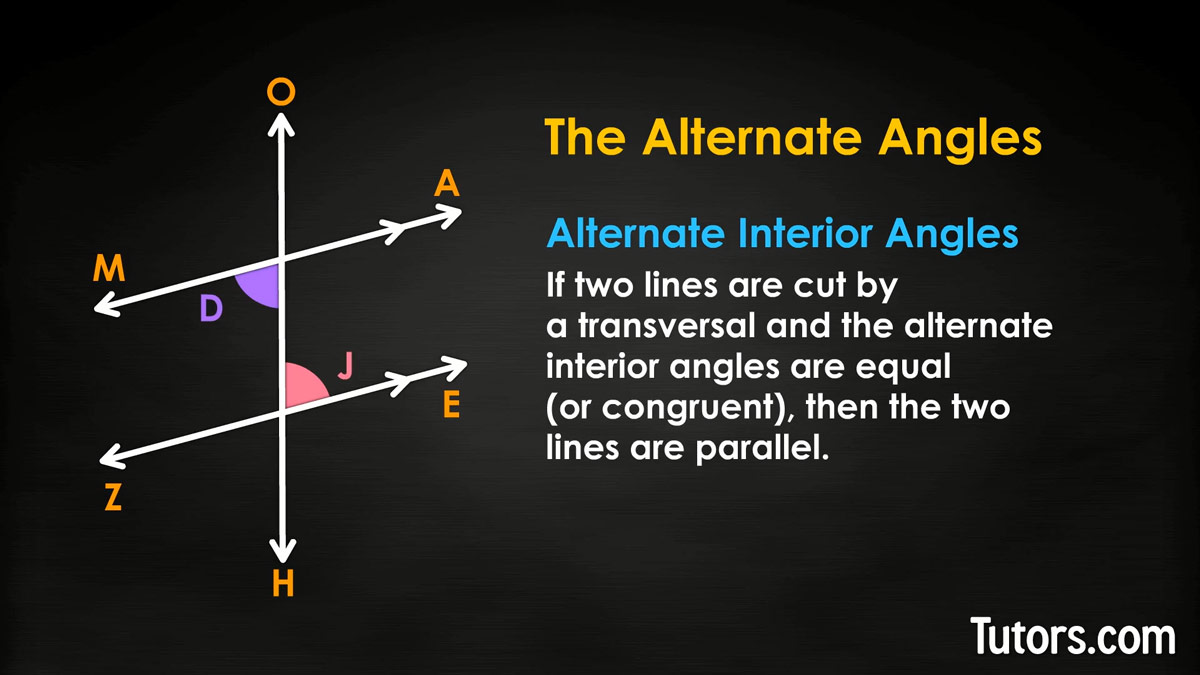
So, in our drawing, if ∠D is congruent to ∠J, lines MA and ZE are parallel. Or, if ∠F is equal to ∠G, the lines are parallel. Again, you need only check one pair of alternate interior angles!
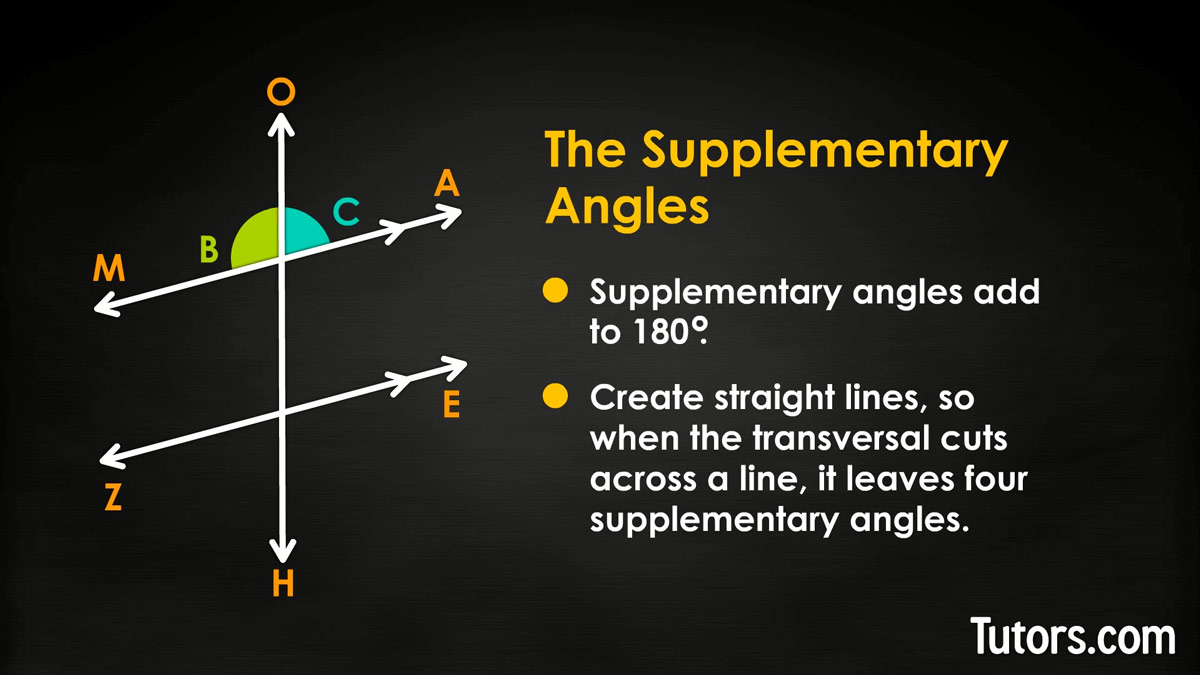
Supplementary angles
Supplementary angles add to 180°. Supplementary angles create straight lines, so when the transversal cuts across a line, it leaves four supplementary angles.
When a transversal cuts across lines suspected of being parallel, you might think it only creates eight supplementary angles, because you doubled the number of lines.
Not true! It creates more than eight!
In our main drawing, can you find all 12 supplementary angles?
Around the top intersection:
∠B and ∠C
∠C and ∠F
∠F and ∠D
∠D and ∠B
Around the bottom intersection:
∠G and ∠J
∠J and ∠L
∠L and ∠K
∠K and ∠G
Those should have been obvious, but did you catch these four other supplementary angles?
∠B and ∠K
∠L and ∠C
∠F and ∠J
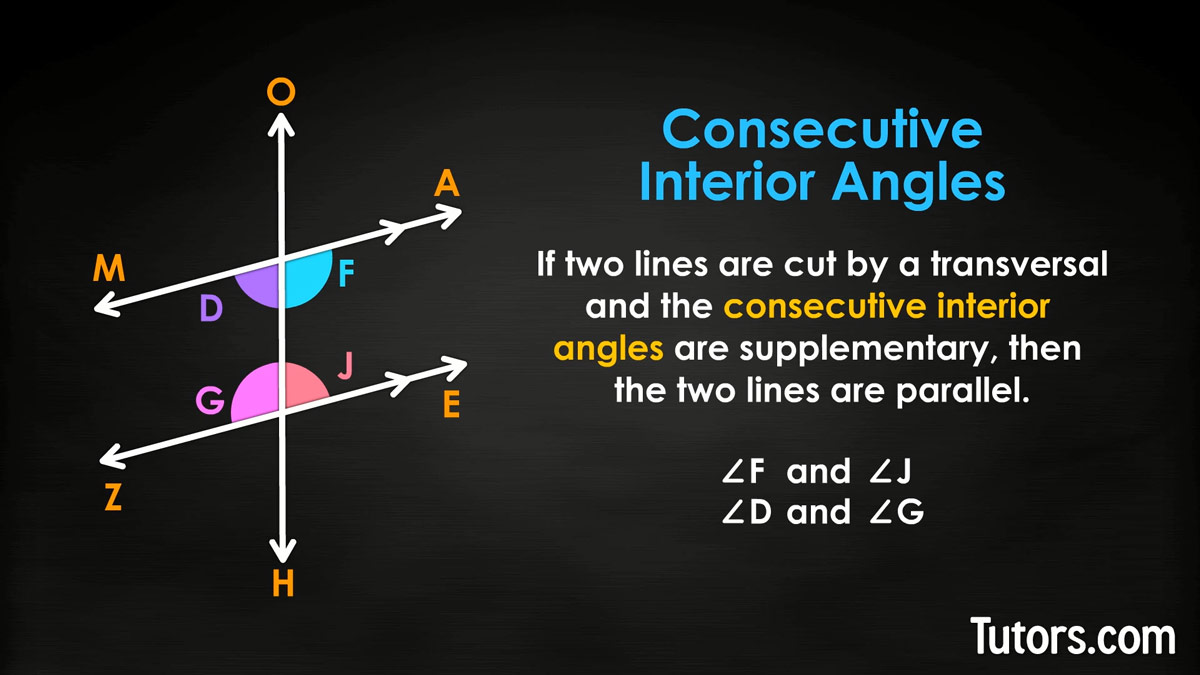
∠D and ∠G
These four pairs are supplementary because the transversal creates identical intersections for both lines (only if the lines are parallel). The last two supplementary angles are interior angle pairs, called consecutive interior angles.
Consecutive interior angle converse theorem
As you may suspect, if a converse Theorem exists for consecutive interior angles, it must also exist for consecutive exterior angles.
Consecutive exterior angle converse theorem
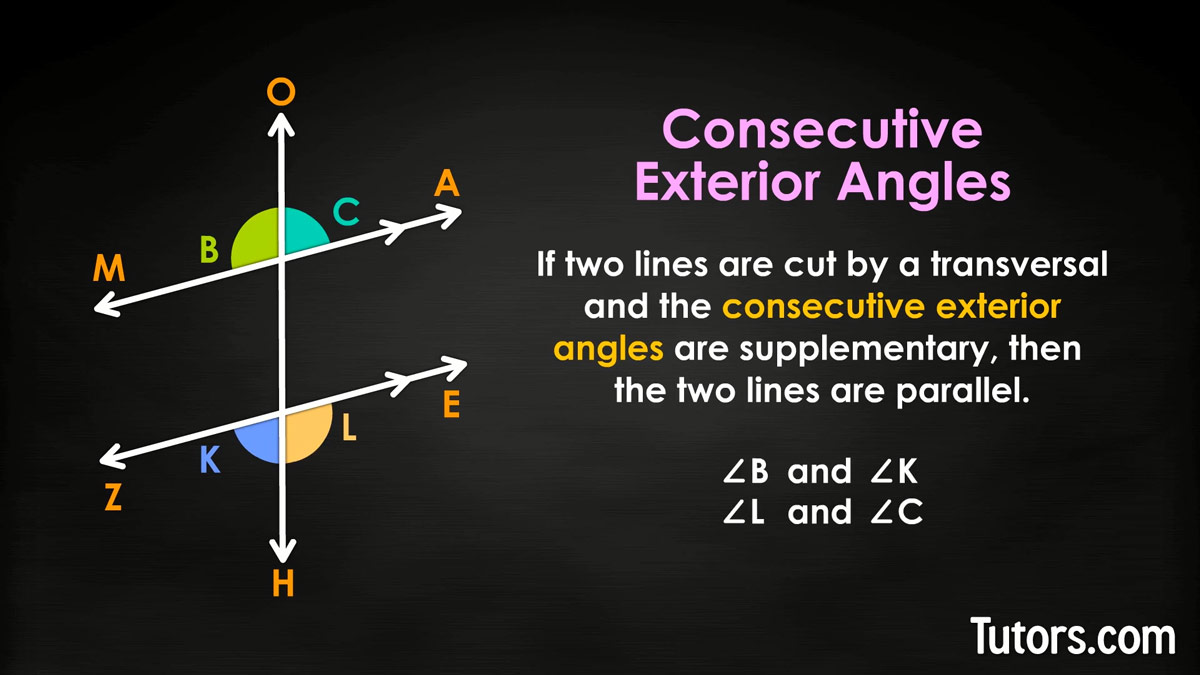
Consecutive exterior angles have to be on the same side of the transversal, and on the outside of the parallel lines. So, in our drawing, only these consecutive exterior angles are supplementary:
∠B and ∠K
∠L and ∠C
Keep in mind you do not need to check every one of these 12 supplementary angles. Just checking any one of them proves the two lines are parallel!
Lesson summary
After careful study, you have now learned how to identify and know parallel lines, find examples of them in real life, construct a transversal, and state the several kinds of angles created when a transversal crosses parallel lines.
Those angles are corresponding angles, alternate interior angles, alternate exterior angles, and supplementary angles. Using those angles, you have learned many ways to prove that two lines are parallel.