Parallel Postulate
How can anyone be sure lines are parallel, if lines go on forever? You and your classmates may be new to geometry, but geometry has existed for thousands of years, and thousands of years ago, Euclid wrote down five postulates, one of which is the kernel of the Parallel Postulate.
What's a postulate?
Euclid had many great ideas, but not all could be proven. A postulate is an idea (also called an axiom) that is taken to be true even without proof. Contrast a postulate with a theorem, which is shown to be true by using proofs.

What are interior angles?
Interior angles are the angles formed when a transversal crosses two other lines. The interior angles are between the two other lines; exterior angles are outside the two other lines. Same-side interior angles are the two angles on the same side of the transversal.
What is the parallel postulate?
After Euclid knocked out four postulates (the foundation for absolute geometry), he waited before springing his fifth postulate, which in an English translation by Thomas Heath states:

Parallel postulate definition
Parallel postulate example
The fastest way to understand the Parallel Postulate is to set up some line segments. Use uncooked spaghetti. Take two strands and arrange them a bit apart from each other but leaning toward each other. Lay a third strand across the first two. You see you have created eight angles at the two intersections.
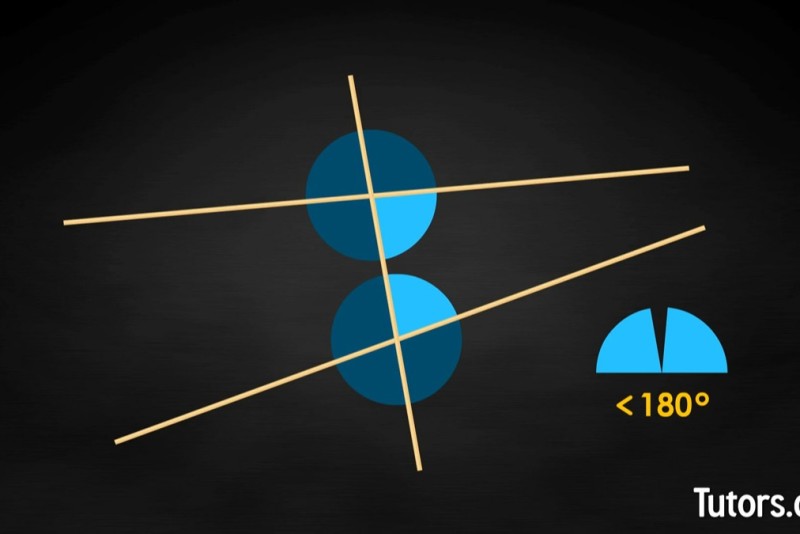
Look at the same-side interior angles toward the close ends of spaghetti.
The sum of both same-side interior angles is less than 180°, so Euclid is saying the lines represented by the first two spaghetti strands will, if extended, eventually meet.
Draw the parallel postulate
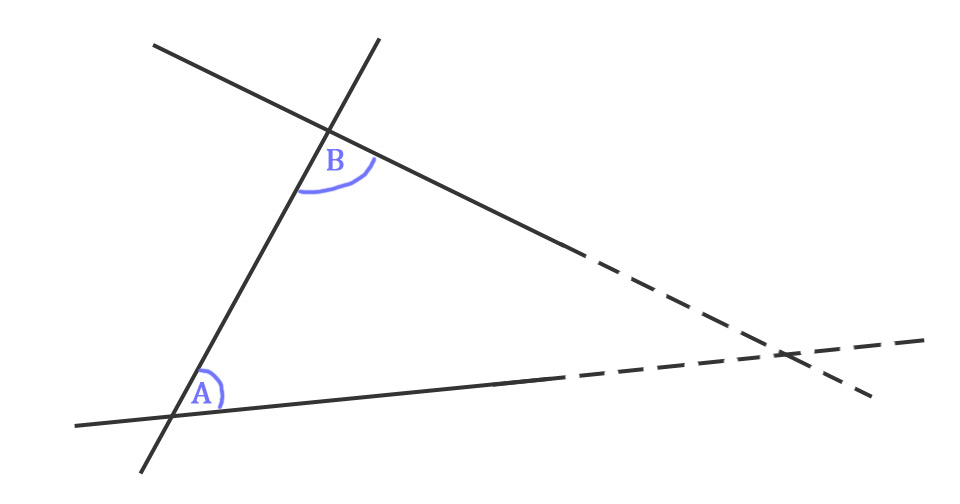
Take a sheet of paper, pencil, and straightedge. Draw a short line, perhaps 10 cm long. Move away a few centimeters from it and draw another 10 cm line. Now draw a transversal (line crossing both of those first two lines). If the two interior angles on the same side add to less than 180°, the drawn lines will, if they continued, meet. Try it. See if they will meet.
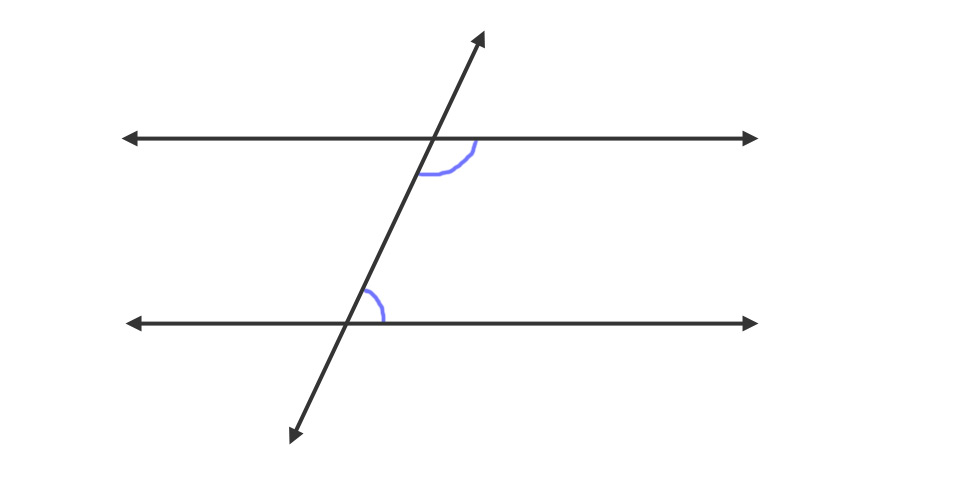
Now start again, but this time, draw two parallel lines. When you draw in the transversal, the two same-side interior angles will either be exactly 90° or will be a combination of an acute and an obtuse angle.
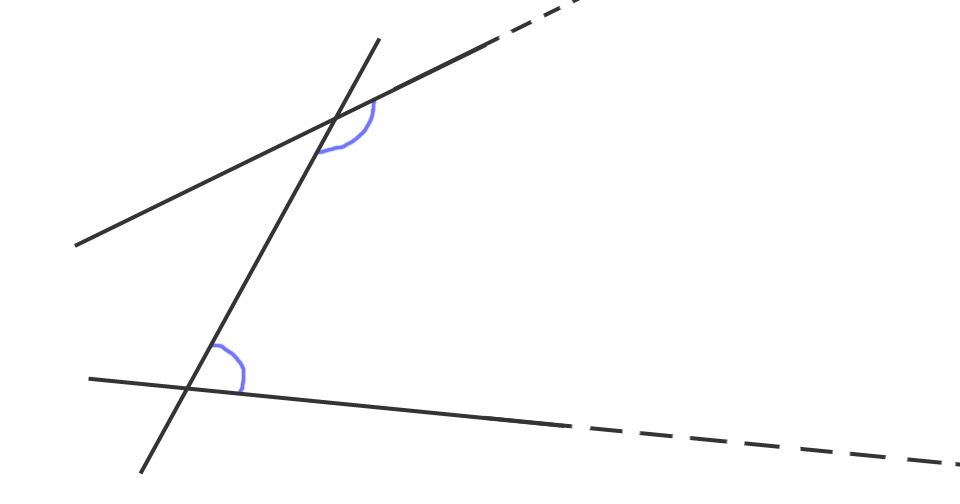
For any line and a point not on that line, Euclid shows us that only one line can be constructed through that point that will be parallel to that line. All other lines will eventually intersect with that original line.
Euclid's parallel postulate
Euclid's Parallel Postulate allows that transversal to create many different angles as it cuts across the two lines, but it all boils down to only three possibilities:
The lines are not parallel and two same-side interior angles are less than 180°; the lines will eventually meet on that side of the transversal.

The lines are not parallel and two same-side interior angles are greater than 180°; the lines will never meet on that side of the transversal.
The lines are parallel and any two same-side interior angles will be equal to 180°; the lines will never meet.

As long as the two interior angles on the same side of the transversal are less than 180° (less than two right angles), the lines will meet. That allows the transversal to even be at a right angle to one of the lines, with the other line creating an acute angle.
Such a situation will create a triangle of the two lines and their transversal, which connects directly to the Pythagorean Theorem.
No matter the combination of lines, transversals, and same-side interior angles, Euclid's Parallel Postulate holds true. Only in the special case of parallel lines will a transversal of any angle create four interior angles such that two same-side interior angles are equal to 180°.
Lesson summary
You have done a lot of work with some very pure ideas. You can now identify and define a postulate, recall and apply Euclid's Parallel Postulate (his fifth postulate), and even test the Parallel Postulate.