Transversal Lines, Angles, & Definition
Transversal lines definition
A transversal is any line crossing another line or lines. When it crosses two parallel lines, the resulting eight angles have interesting properties.
You have probably ridden in a car on a street that crossed railroad tracks. As you crossed the tracks, you completed a transversal. A transversal is a line that crosses other lines. Usually we work with transversals when they cross parallel lines, like the two tracks of a railroad.
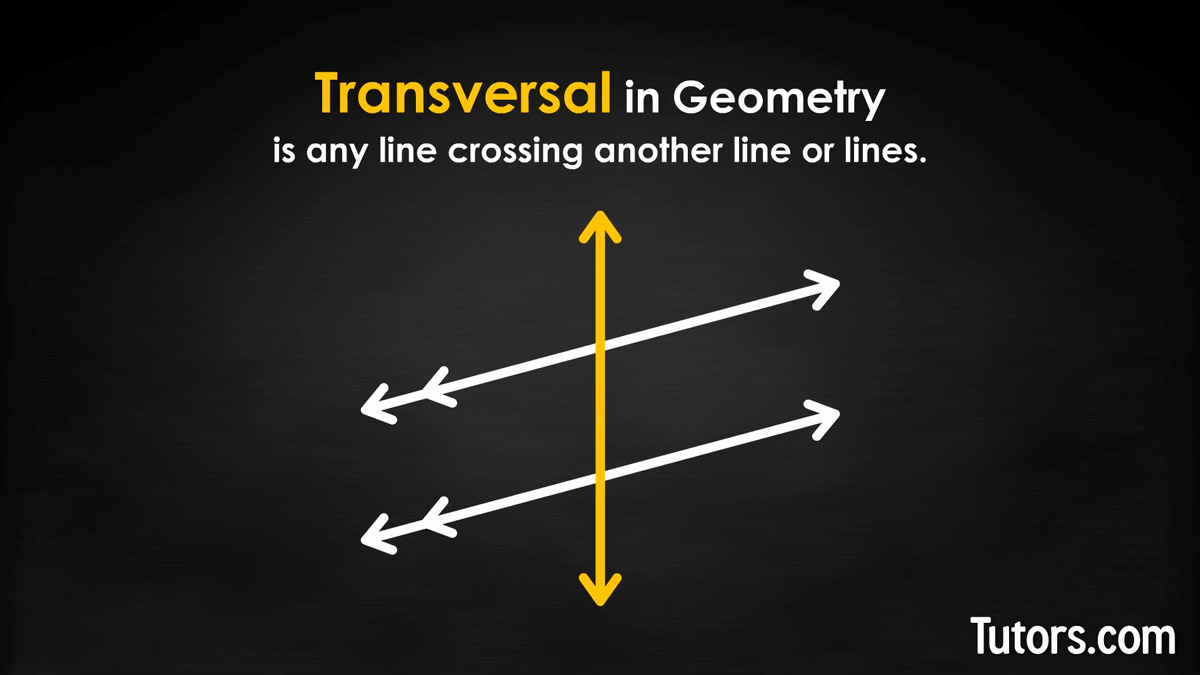
Parallel lines cut by a transversal
Let's construct a transversal to see how they interact with parallel lines. Use a straightedge and pencil to draw parallel lines BE and AR, so that BE is horizontal and at the top, with AR horizontal and at the bottom.
Use a straightedge and pencil to draw a line cutting from above BE to below AR. Label it OW. You see? It is never a good idea to cross a bear.
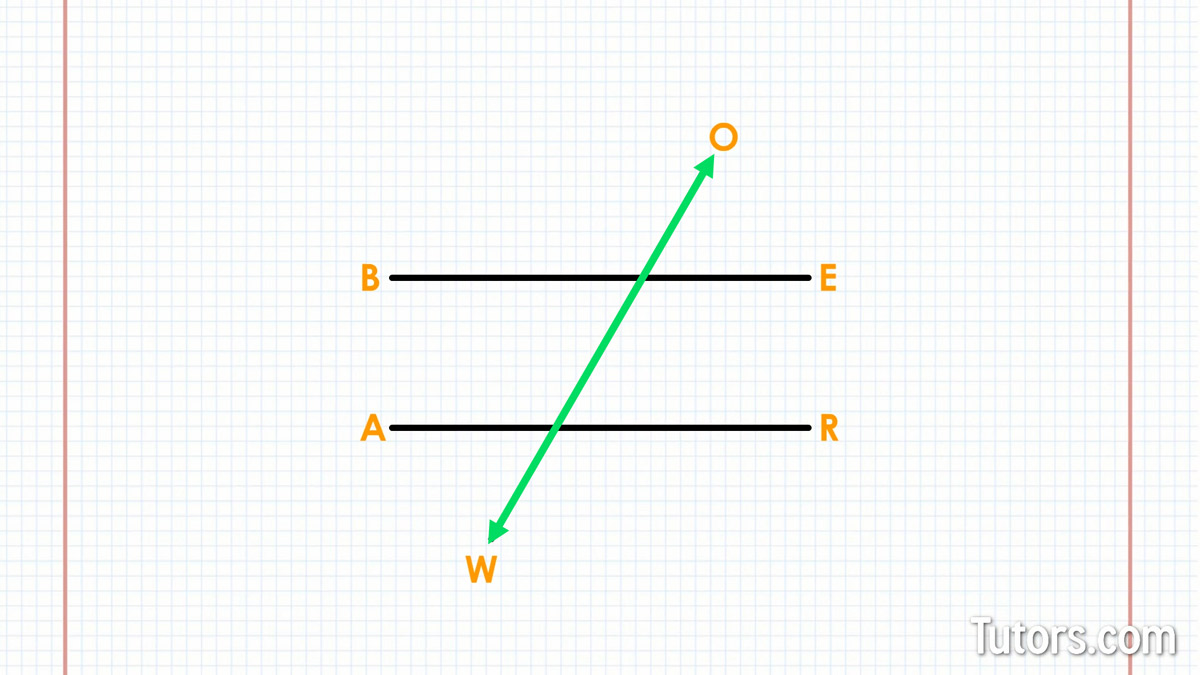
Transversal angles
Our transversal OW created eight angles where it crossed BE and AR. These are called supplementary angles.
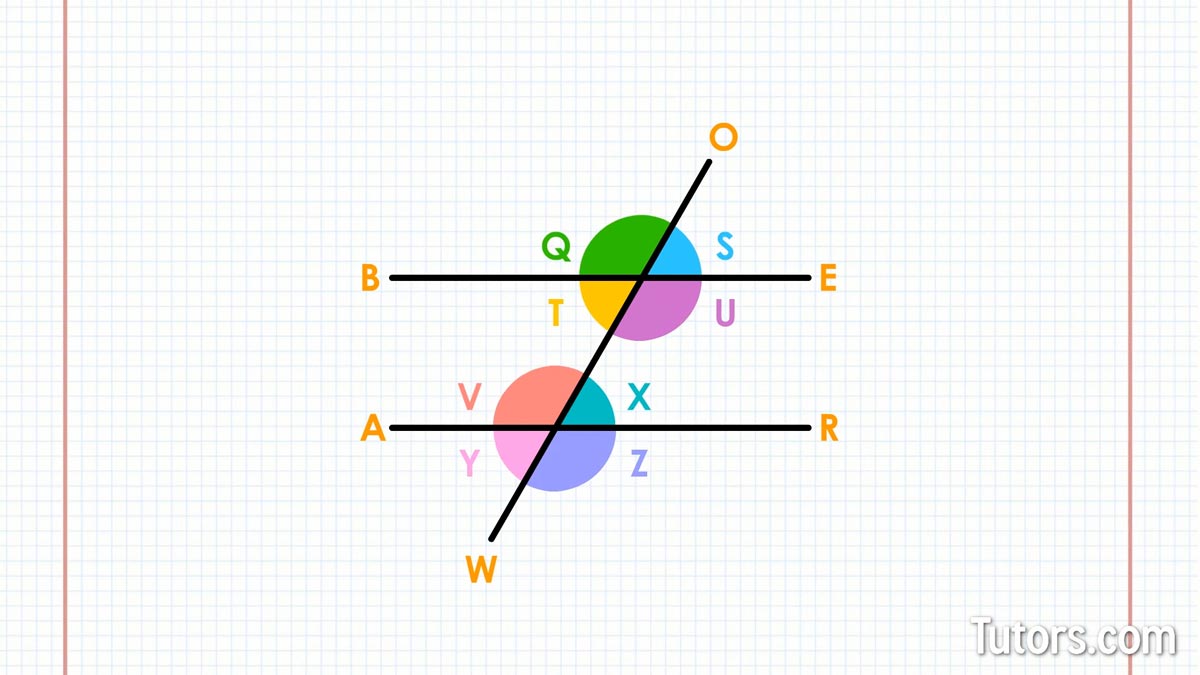
Supplementary angles
Supplementary angles are pairs of angles that add up to 180°. Because all straight lines are 180°, we know ∠Q and ∠S are supplementary (adding to 180°). Together, the two supplementary angles make half of a circle. Supplementary angles are not limited to just transversals.
In this example, the supplementary angles are QS, QT, TU, SU, and VX, VY, YZ, VZ.
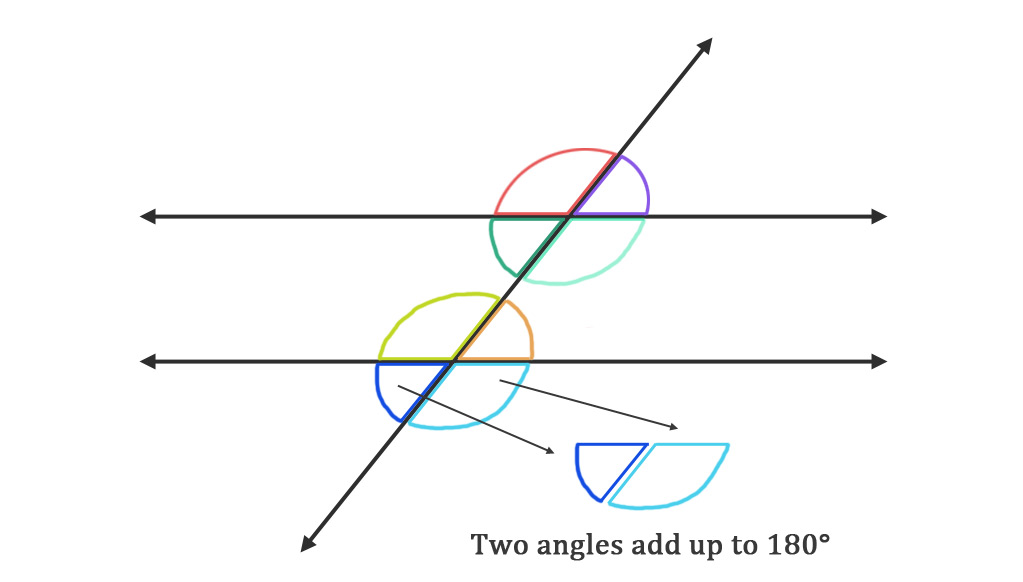
Here are all the other pairs of supplementary angles:
∠Q supplementary to ∠S
∠Q supplementary to ∠T
∠T supplementary to ∠U
∠S supplementary to ∠U
∠V supplementary to ∠X
∠V supplementary to ∠Y
∠Y supplementary to ∠Z
∠V supplementary to ∠Z
Exterior angles
Think back to those railroad tracks. If you were between the train tracks, you would be inside the lines. If you stepped across the tracks, you would be outside the lines.
The same is true with parallel lines BE and AR and their transversal OW. The angles above and below the parallel lines are outside and are called exterior angles.
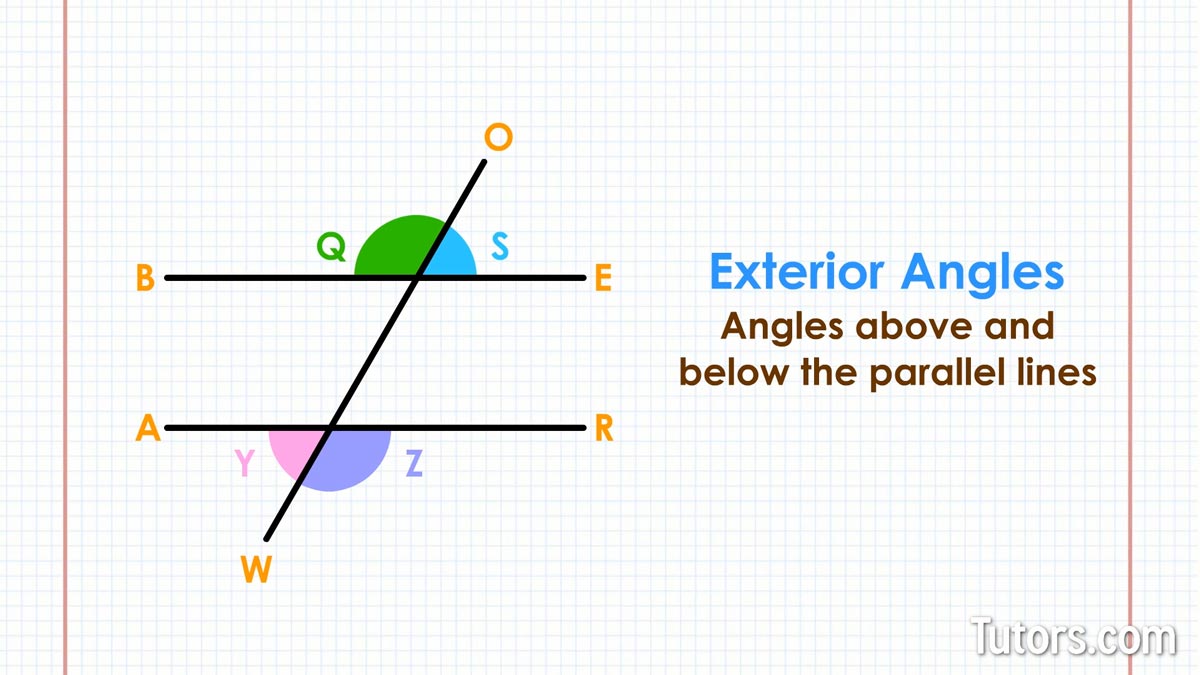
Your drawing has four exterior angles: ∠Q, ∠S, ∠Y and ∠Z.
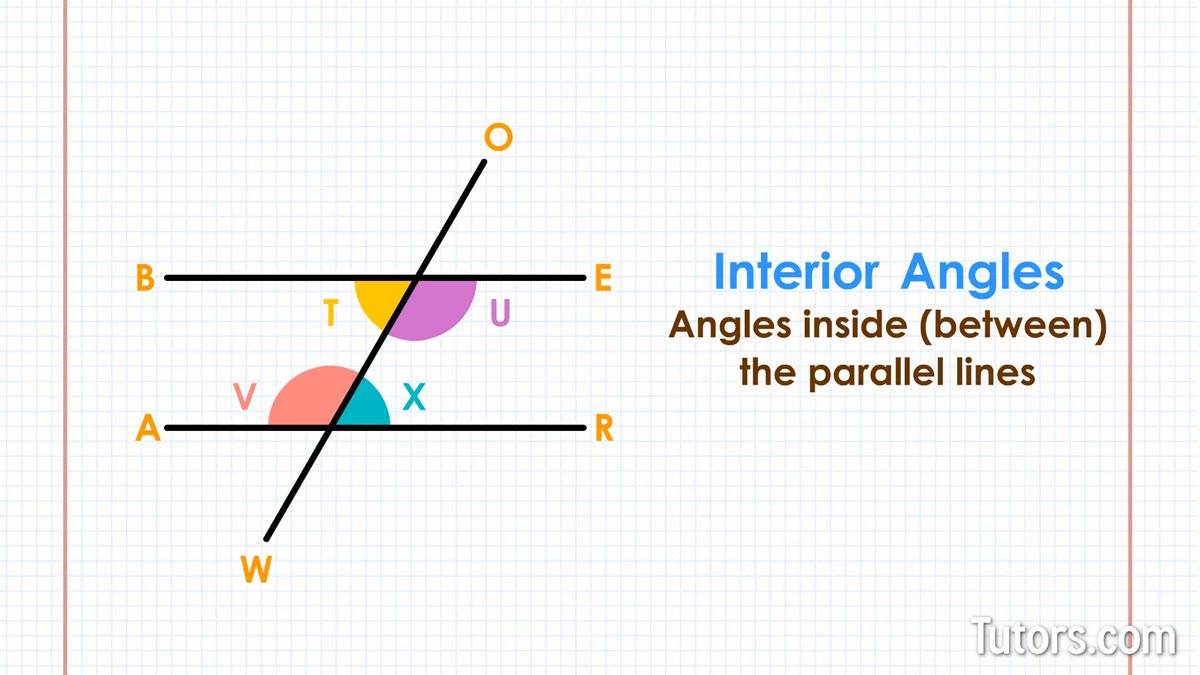
Interior angles
Your drawing also has four interior angles, or angles inside (between) the parallel lines: ∠T, ∠U, ∠V and ∠X.
Vertical angles
Angles in your transversal drawing that share the same vertex are called vertical angles. Do not confuse this use of "vertical" with the idea of straight up and down.
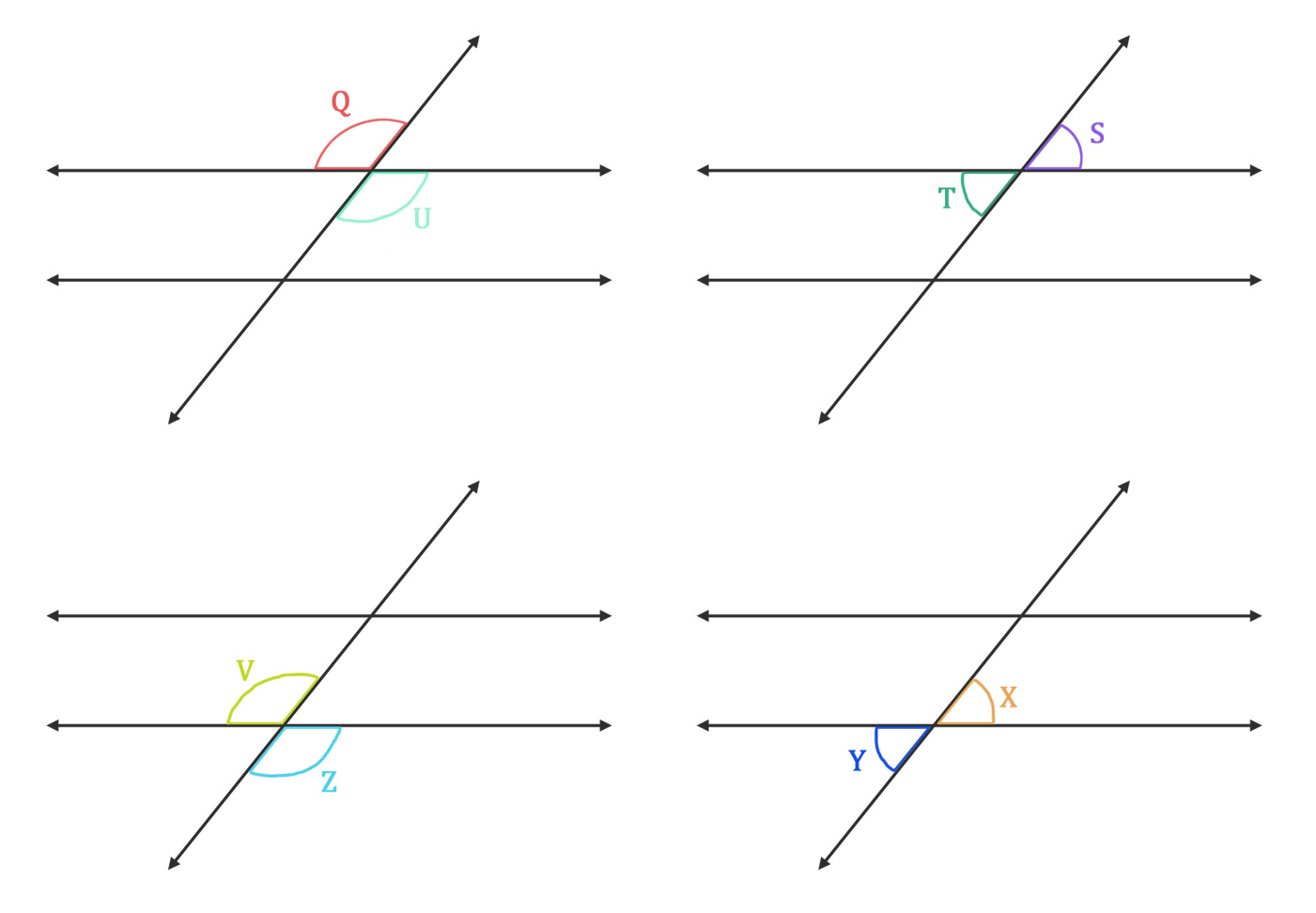
When two parallel lines are crossed by a transversal, you get four pairs of vertical angles:
∠Q and ∠U
∠S and ∠T
∠V and ∠Z
∠Y and ∠X
Corresponding angles
The two parallel lines are creating corresponding angles. To be corresponding angles they must be on the same side of the transversal and one angle must be interior and the other exterior.
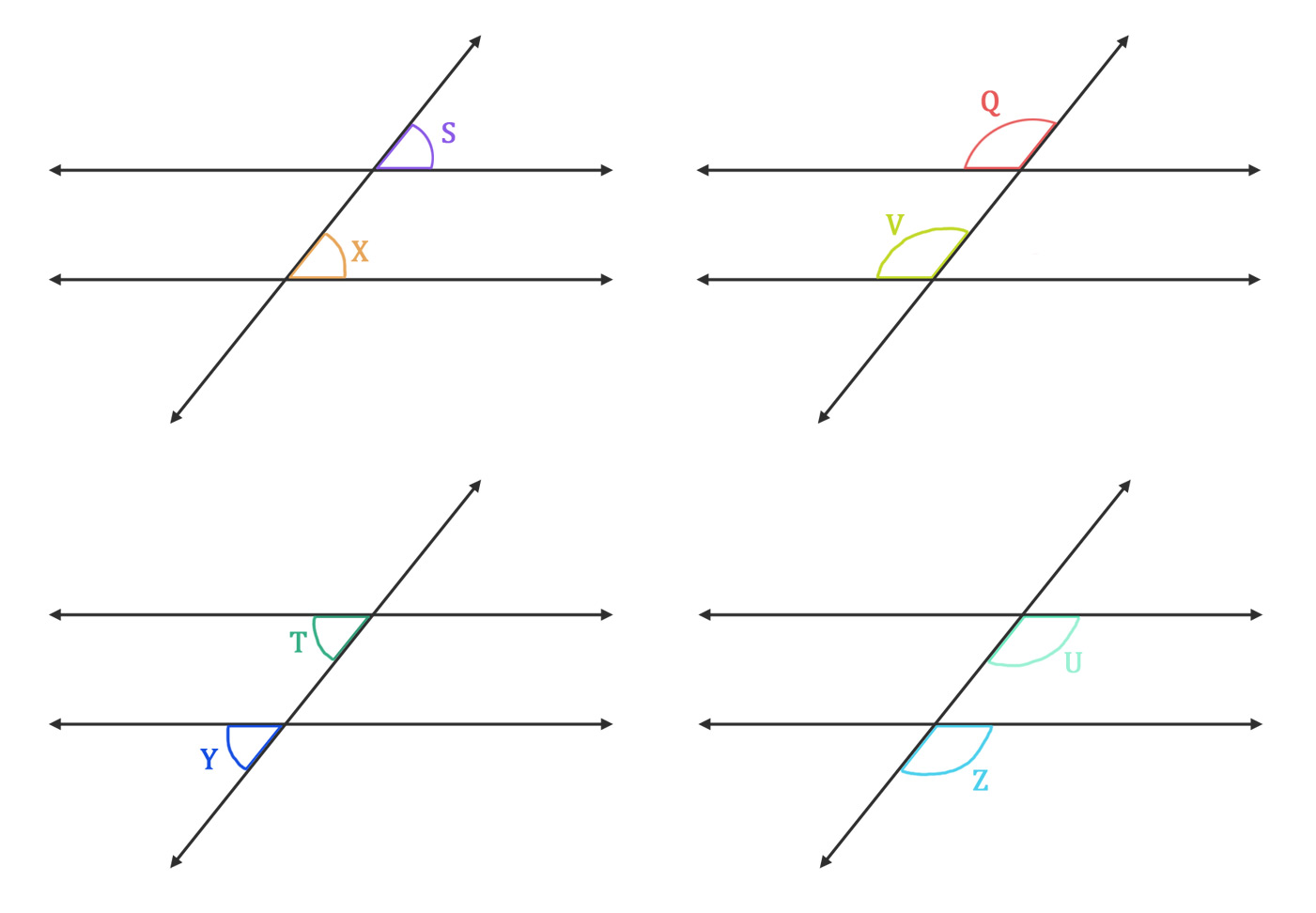
Notice that ∠Q is congruent to ∠V. ∠Q is an exterior angle on the left side of transversal OW, and ∠V is an interior angle on the same side of the transversal line.
All the pairs of corresponding angles are:
∠Q and ∠V
∠T and ∠Y
∠S and ∠X
∠U and ∠Z
Alternating angles
Alternating angles are pairs of angles in which both angles are either interior or exterior. They appear on opposite sides of the transversal and are congruent.
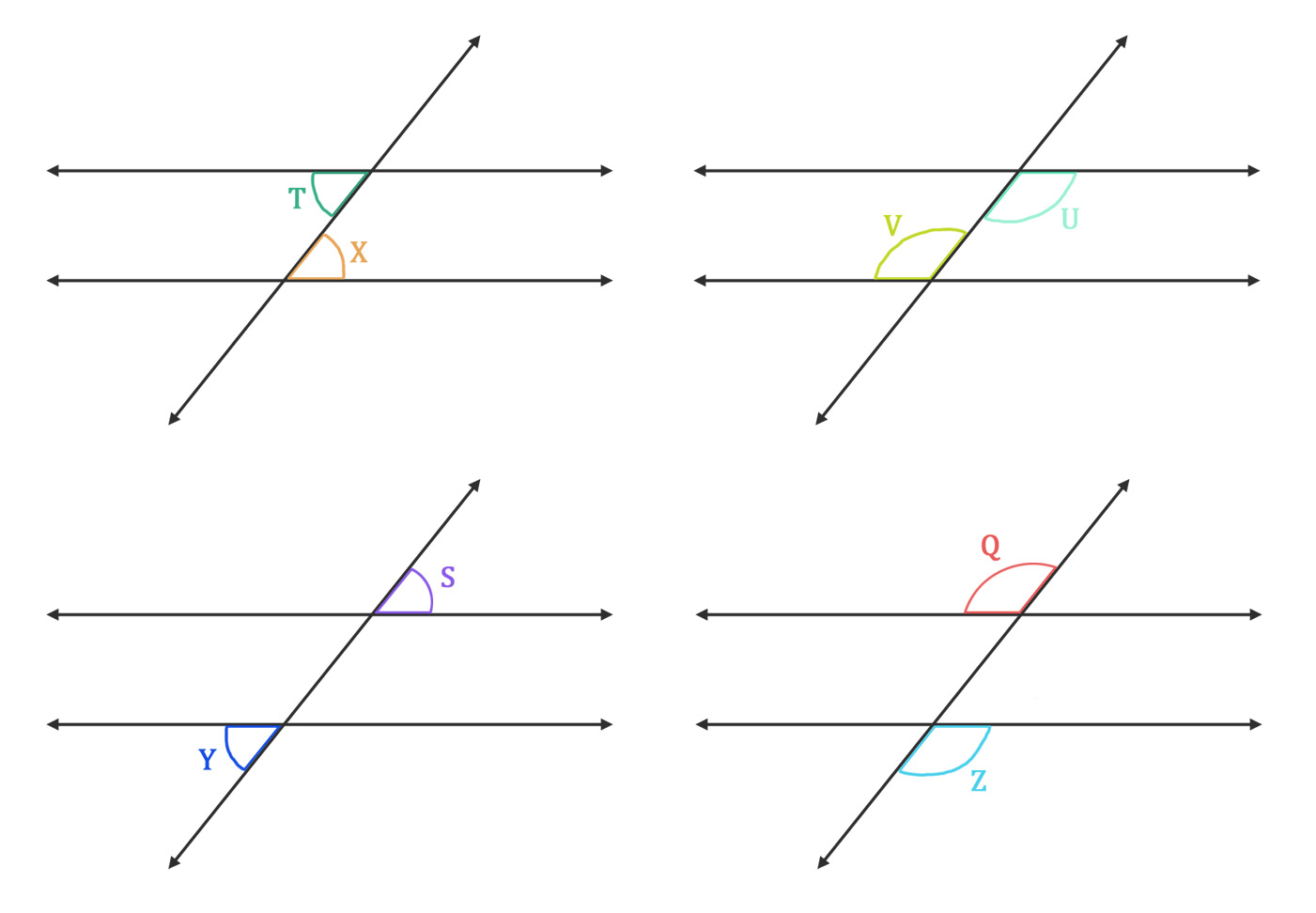
The four pairs of alternating angles in our drawing are:
∠V and ∠U (interior)
∠X and ∠T (interior)
∠Q and ∠Z (exterior)
∠Y and ∠S (exterior)
There are to pairs of alternate interior angles, and two pairs of alternate exterior angles.
Alternate interior angles have their own their theorem to help identify information about the angles themselves. Alternate exterior angles also have their own theorem.