Parallel and Perpendicular Lines
Coplanar lines
Any two flat objects sharing space on a plane surface are said to be coplanar. Three types of lines that are coplanar are parallel lines, perpendicular lines, and transversals. These all exist in a single plane, unlike skew lines (which exist in multiple planes). Any two lines in a plane must necessarily either be parallel or intersect.
Parallel lines
Parallel lines never meet, despite co-existing in a plane and continuing in two directions forever. Measure the distance between the two lines anywhere along their lengths, as many times as you like; they will always be the same distance apart.
Slope of parallel lines
If we apply coordinate geometry to parallel lines, we can see through the parallel lines equations that parallel lines will have the same slope:
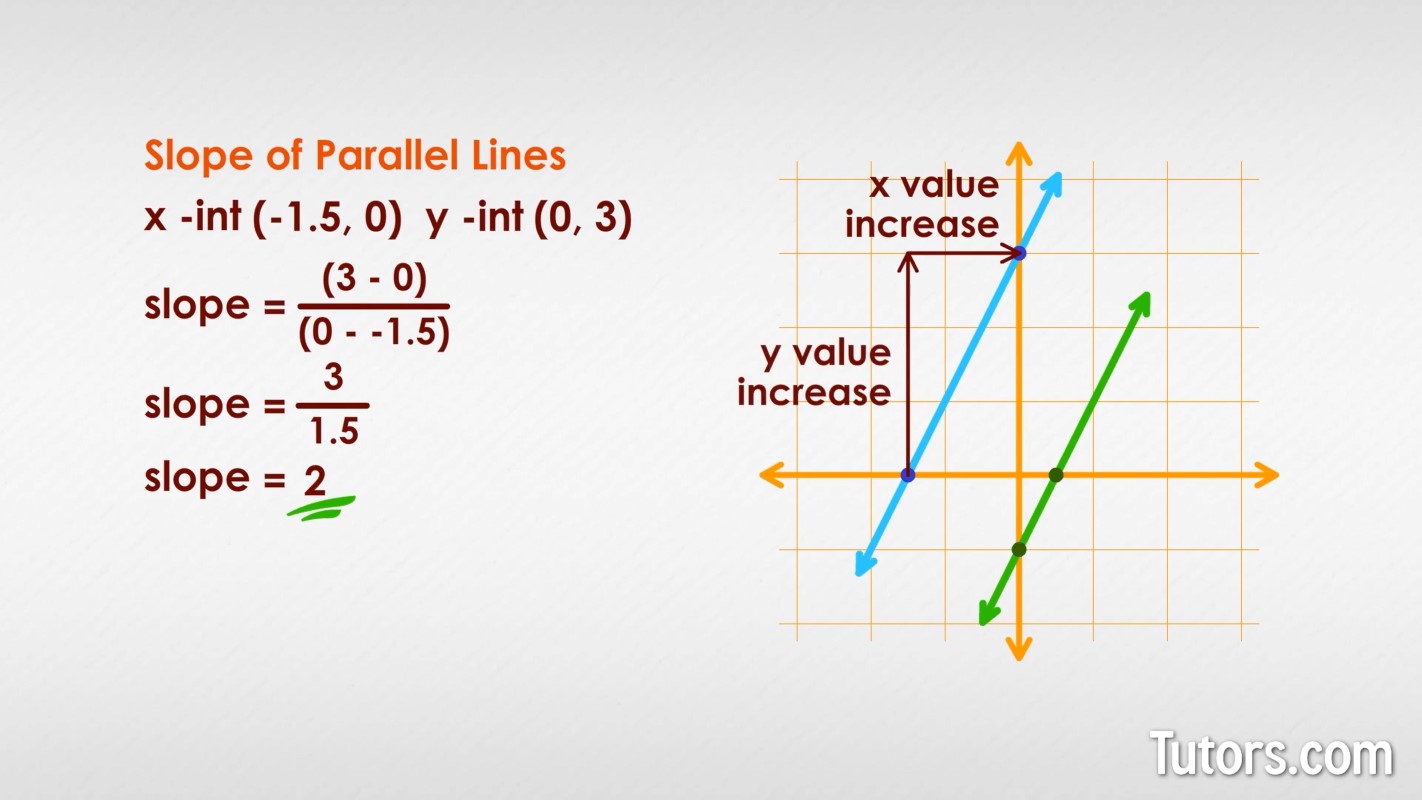
The lower line intercepts the xx axis at 0.5, at (0.5, 0) and the y axis at (0, -1). Slope is rise (change in y-value) over run (change in x-value), so for the lower line:
The upper line has an x-intercept of -1.5 (-1.5, 0) and a y-intercept of 3 (0, 3), so its slope is:
With positive slopes, the two values increase together (x-values increase as y-values increase).
Parallel line examples
Examples of parallel lines outside of coordinate graphs are everywhere. Floor boards, window blinds, notebook paper lines, painted line segments in a parking lot -- all parallel lines. Nobody expects you to apply slope formulas to diagonal parking lines, but you can find coplanar parallel lines in your everyday life.
Perpendicular lines
Coplanar lines that are not parallel must intersect or cross each other. They can intersect at any angle, but when the lines intersect at exactly 90° they are perpendicular lines. Perpendicular lines create four right angles at their point of intersection.
Slope of perpendicular lines
When plotting perpendicular lines on a coordinate graph, you need to consider two ideas:
The slopes will be opposites
The slopes will be reciprocals
Let's take the first requirement: opposite slopes. We'll keep one of our earlier lines with a positive slope of 2, and then show a new, second line with a negative slope of -2:
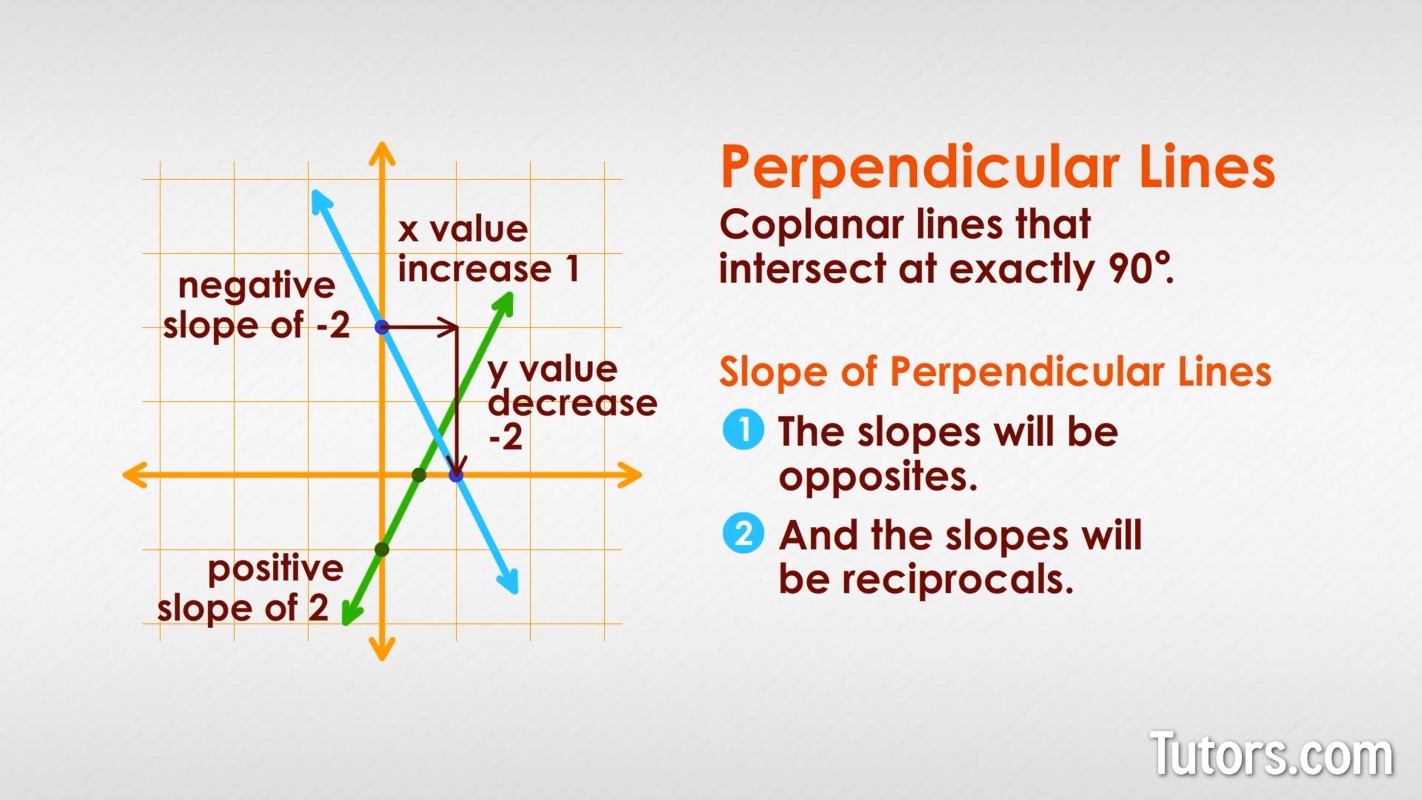
Now the lines are crossing, with our new line showing x-values increasing as y-values are decreasing. Negative slopes have that inverse relationship between the x-values and y-values. But our intersecting lines are not perpendicular, yet.
The slopes must be reciprocal, so instead of simply having one with a positive slope of 2 and one with a negative slope of -2, we need the second line to be (the reciprocal of ):
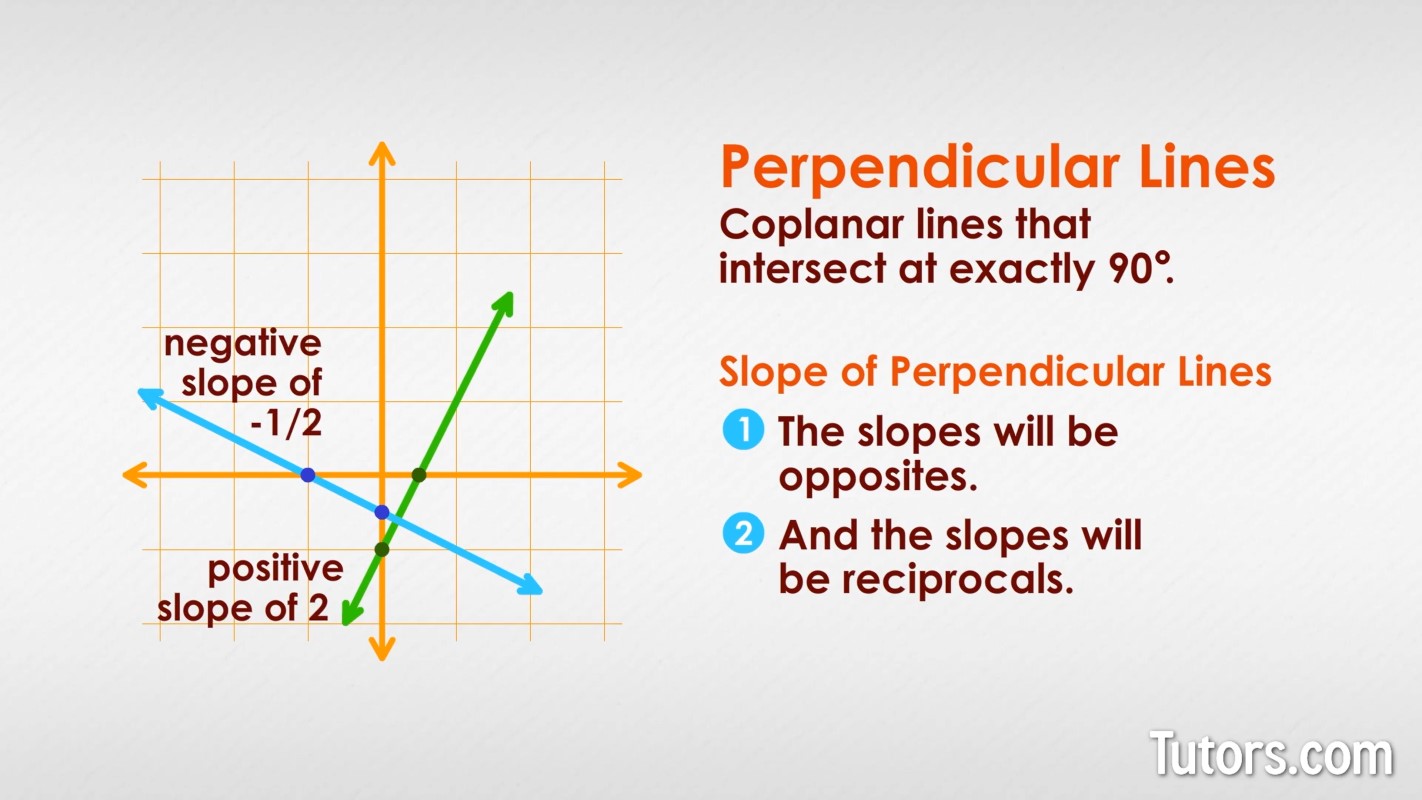
Like parallel lines, examples of perpendicular lines surround us, in walls meeting floors and ceilings, in floor tiles, in bricks in walls, in window grilles. The margin line on a sheet of notebook paper is perpendicular to the parallel writing lines.
Parallel and perpendicular line equations
Can you tell if these lines are perpendicular or parallel given these equations? If the slopes are equal, the lines will be parallel. If the slopes are opposite reciprocals of each other, the lines will be perpendicular. Try these three examples:
Line F is
Line O is
Line X is
Lines F and X are parallel, separated only by a difference of 1. The fraction simplifies to ; adding the 1 moves Line X one unit away from Line F. Line O is perpendicular to Lines F and X because it has the negative reciprocal of .
Transverse lines or transversals
Coplanar lines that intersect other coplanar lines are called transverse lines or transversals. A transversal crossing two parallel lines creates eight angles, which can be viewed and compared many ways:
Two pairs of consecutive interior angles
Two pairs of alternate interior angles
Two pairs of alternate exterior angles
Two pairs of consecutive exterior angles
Four pairs of corresponding angles
Transverse lines are everywhere in nature and human-made objects. Street maps show parallel, perpendicular and transverse lines. Mown hay lies in bundles of transverse lines, with any three strands being coplanar. A handful of casually tossed pencils will crisscross as transverse lines.