What are Parallel Lines?
Parallel lines definition
Parallel lines are two or more lines that are the same distance apart, never merging and never diverging. We recall that lines are never-ending, so parallel lines continue forever in two directions. They don't have to be straight lines, as long as they are always the same distance apart.
The English word "parallel" is a gift to geometricians, because it has two parallel lines in it, in the form of the two side-by-side ls. It reminds you of what it means!

A single existing line can have an infinite number of parallel lines, too, simply by picking a point, not on any existing line, and constructing a line parallel to all the existing ones. To be parallel lines, both lines must exist in the same plane; they must be coplanar. This differentiates them from skew lines, which exist in three dimensions (two separate planes).
Parallel shapes
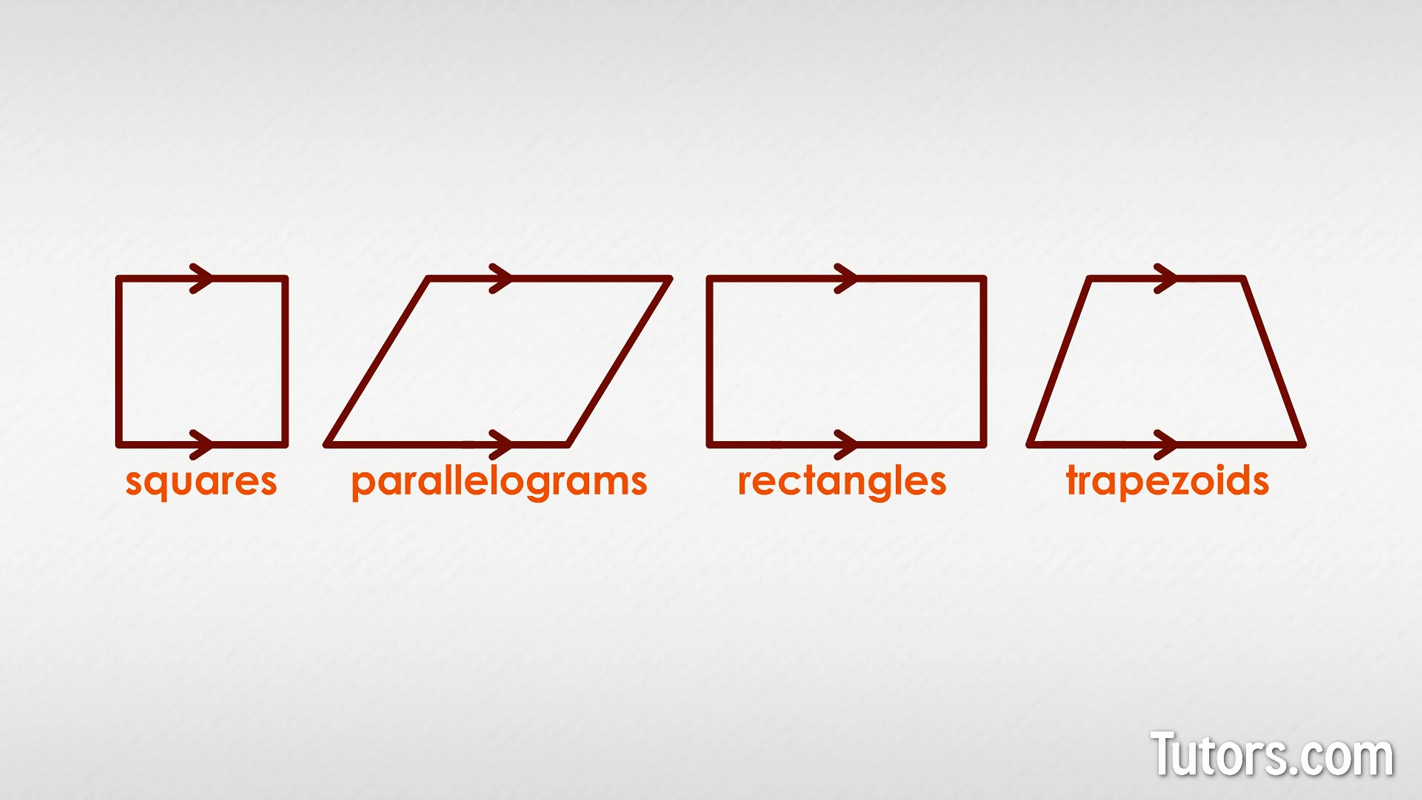
Parallel lines are by themselves very interesting, but when you take segments of them, you can construct many polygons. Think of squares, parallelograms, rectangles, and trapezoids; they all have parallel sides made from parallel line segments.
Parallel symbol
To symbolize parallel lines in geometry, we use two vertical lines (or slightly slanted lines), like this:
AT || UP
AT // UP
Both of those statements tell us that line AT is parallel to line UP.
How to construct parallel lines
Construct parallel lines with a straightedge, a pencil, and plain paper. If using a ruler, this is a one-step process. Lay the ruler on the paper, holding it carefully, so it does not slip. Trace each edge of the ruler. You're done!
When you move the ruler, you have parallel lines. You can label them, identifying each line with two named points and placing arrowheads at the end of the two lines.
You can also construct a line parallel to an existing line passing through a single point, not on the line. You need a drawing compass plus the plain paper, pencil, and straightedge.
For the given line, draw a transversal crossing the existing line and passing through the point not on the line; we'll call that Point A (for Above!). Now, you have two intersecting lines. Identify the point where your new transversal intersects the existing line; call it Point N (for New!)
Set your drawing compass to scribe an arc shorter than the distance from the existing line to Point A.
Scribe two arcs with the compass needle set on Point N and again on Point A. The first arc, from Point N, should cross the existing line and the transversal; the second arc, from Point A, will cross only the transversal somewhere above Point A.
Where your first arc crosses the transversal below Point A, place your compass needle on the transversal and adjust the compass to reach the point on the existing line where your first arc crossed it.
Lift the compass, and without adjusting it, place the needle on that point above Point A where the second arc intersected the transversal.
Scribe another arc down to cross that second arc.
Where the two arcs cross near Point A, connect that point to Point A to construct a line parallel to your existing line.
Graphing parallel lines
In coordinate graphing, parallel lines are easy to construct using the grid system. A simple equation can provide all the information you need to graph a line:
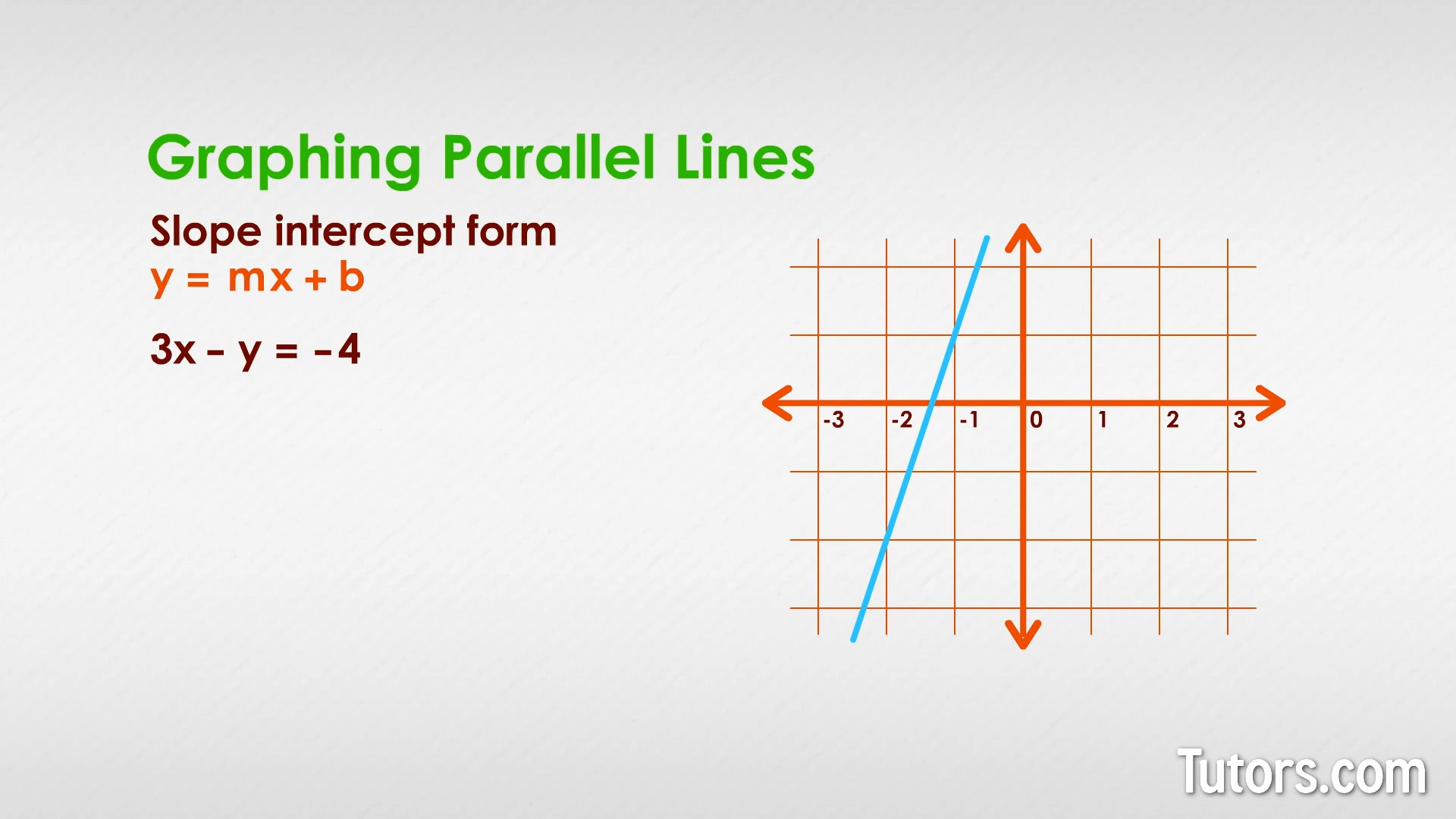
Our line is established with the slope-intercept form, y = mx + b. So we solve the first equation, so it is changed to the slope-intercept form:
To solve for y we subtract 3x from both sides, simplify, and then divided both sides by -1:
Now add another line that keeps the x-value the same. You only need to retain 3x, so you could write:
This new line is far to the right of the first line but is exactly parallel because the x-value determined its slope. Same x-value; same slope; both lines parallel!
Real-Life examples of parallel lines
Parallel lines rule the construction industry. Buildings are erected with walls parallel to each other, ceilings are parallel to floors, and one building is usually put up parallel to other buildings on the same block.
Notebook paper is a thick collection of parallel lines. When your notebook is closed, the lines are not only parallel on each page, they are parallel from page to page, too.
Parallel lines as a purely geometric concept must be completely flat and exist on a single plane. In real life, while railroad tracks, the edges of sidewalks, and the markings on streets are all parallel, the tracks, sidewalks, and streets go up and down hills and around curves. Those three real-life examples are good, but not perfect, models of parallel lines.
Consider railroad tracks. The two lines never meet, but they move up and down and side to side through three-dimensional space. Railroad tracks, unless they are on a completely flat plain like a desert, are more similar to skew lines than parallel lines.