Supplementary Angles — Definition, Examples & How to Find

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What is a supplementary angle?

Angles and angle pairs are everywhere in geometry. Two types of angle pairs are complementary angles and supplementary angles.

• Supplementary angles sum to exactly 180° or exactly $\pi$ radians.

• Complementary angles sum to exactly 90° or exactly $\frac{\pi }{2}$ radians.

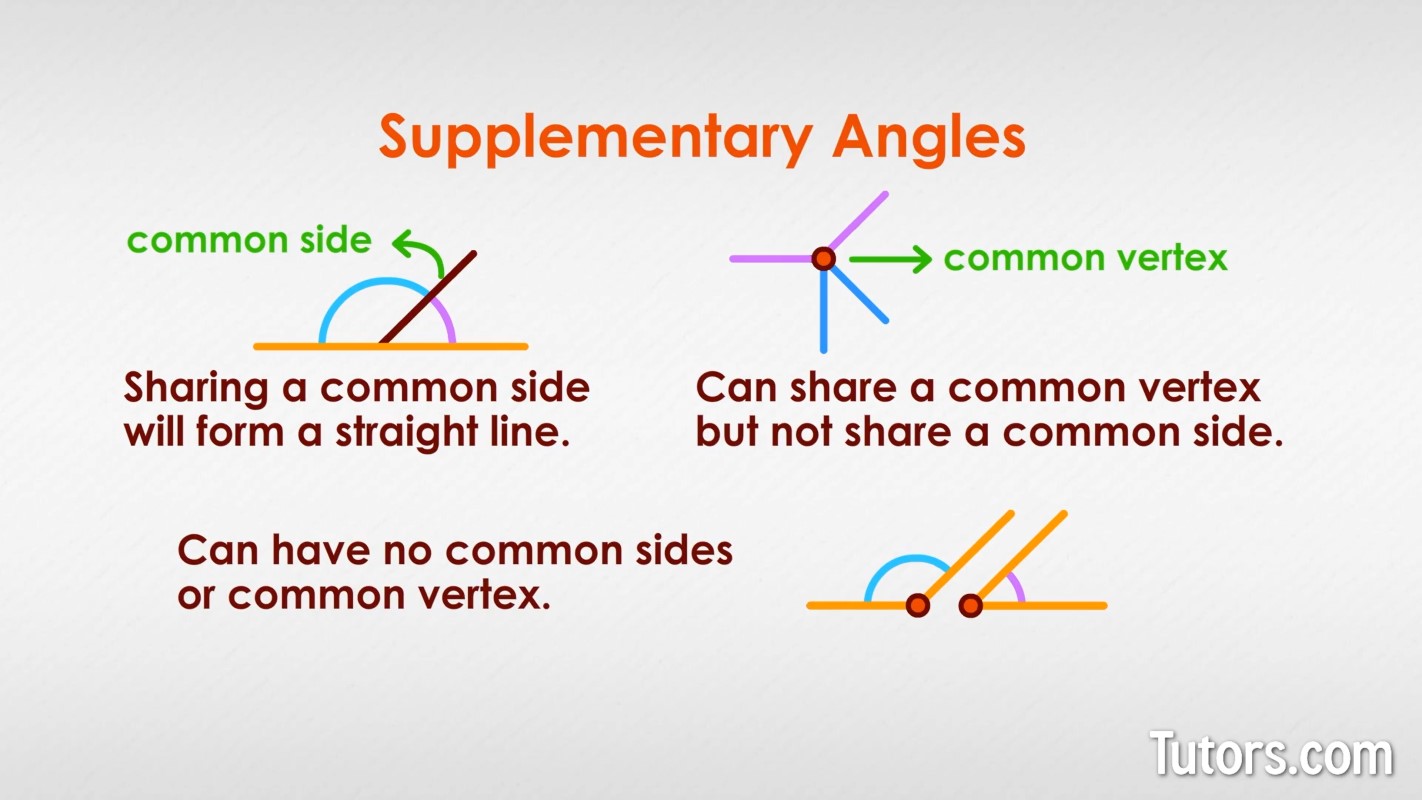
Supplementary angles are easy to see if they are paired together, sharing a common side. Supplementary angles sharing a common side will form a straight line.

Supplementary angles can also share a common vertex but not share a common side.

Supplementary angles can also have no common sides or common vertex.

Four angle types

Four types of angles in geometry are:

1. Acute angles - measuring less than 90° or less than $\frac{\pi }{2}$ radians

2. Obtuse angles - measuring greater than 90° or greater than $\frac{\pi }{2}$ radians

3. Right angles - measuring exactly 90° or exactly $\frac{\pi }{2}$ radians

4. Straight angles - measuring exactly 180° or exactly $\pi$ radians

Properties of supplementary angles

Supplementary angles have two properties:

1. Only two angles can sum to 180°- three or more angles may sum to 180° or $\pi$ radians, but they are not considered supplementary

2. The two angles must either both be right angles, or one must be an acute angle and the other an obtuse angle

Try it!

Here are eight sets of angles in degrees. Identify the ones that are supplementary:

1. 175° and 5°

2. 137° and 93°

3. 60° and 60° and 60°

4. 26° and 116°

5. 90° and 90°

6. 85° and 95°

7. 150° and 31°

8. 100° and 80°

Notice the only sets that sum to 180° are the first, fifth, sixth and eighth pairs. Only those pairs are supplementary angles. The third set has three angles that sum to 180°; three angles cannot be supplementary.

Theorems

Supplementary angles are seen in three geometry theorems. Two theorems involve parallel lines.

Congruent Supplements Theorem says that If two angles - we'll call them $\angle C$ and $\angle A$ - are both supplementary to a third angle (we'll call it $\angle T$), then $\angle C$ and $\angle A$ are congruent.

We know two true statements from the theorem:

1. $\angle A+\angle T=180°$

2. $\angle C+\angle T=180°$

Since either $\angle C$ or $\angle A$ can complete the equation, then $\angle C=\angle A$.

Same Side Interior Angles Theorem states that if a transversal intersects two parallel lines, then the interior angles on the same side of the transversal are supplementary.

A transversal through two lines creates eight angles, four of which can be paired off as same side interior angles.

The converse of the Same Side Interior Angles Theorem is also true. The converse theorem tells us that if a transversal intersects two lines and the interior angles on the same side of the transversal are supplementary, then the lines are parallel.

This is an especially useful theorem for proving lines are parallel. Here are two lines and a transversal, with the measures for two same side interior angles shown:

Since the converse of the theorem tells us the interior angles will be supplementary if the lines are parallel, and we see that $145°-35°=180°$, then the lines must be parallel.

Consecutive Angles in a Parallelogram are Supplementary - One property of parallelograms is that their consecutive angles (angles next to each other, sharing a side) are supplementary.

Here is parallelogram MATH:

Whatever angle you choose, that angle and the angle next to it (in either direction) will sum to 180°. Go ahead, try it!

This property stems directly from the Same Side Interior Angles Theorem, because any side of a parallelogram can be thought of as a transversal of two parallel sides.

Supplementary angles examples

A common place to find supplementary angles is in carpentry. Miter boxes, table saws, and radial arm saws all depend on the user's quick mental math to find the supplementary angle to the desired angle.

Say you need a 120° angle. You will only see numbers on those saws from 10° to 90°. You need to know 180° − 120° = 60°, so you set the saw for a 60° cut on the waste wood, leaving 120° on the piece you want.

Supplementary angles also reveal themselves in repeated patterns, where right angles form windows, bricks, floor tiles, and ceiling panels. Many field stone walls have supplementary angles in them. Look around; you will see supplementary angles everywhere!