Angle Pairs | Types of Angle Pairs

What are Angle Pairs?

Angle pairs are called that because they always appear as two angles working together to display some unusual or interesting property. We will look at nine different types of angle pairs.

Table Of Contents

1. Adding to 90°
2. Adding to 180°
3. Congruent Angle Pairs
4. Special Pairs
5. Not-So-Special Pairs

Adding to 90°

Complementary angle pairs add to 90°. These pairs do not have to be touching to be complementary. Any two angles that sum to 90° are complementary angle pairs:

Any two right angles will always be complementary and congruent, whether or not they share a common vertex or common side.

Adding to 180°

Two interesting varieties of angle pairs sum to 180°. These are linear pairs and supplementary angles.

Linear pairs get their name because the sides not common to the two angles form a straight line. Linear pairs always share a common vertex and one common ray, line segment, or line. Linear pairs are always supplementary and adjacent angles.

Linear pairs always form when lines intersect. Just two intersecting lines creates four linear pairs. Every pair shares a vertex, the point of intersection, and one common side.

See if you can find the four linear pairs in intersecting lines MAP and TAN:

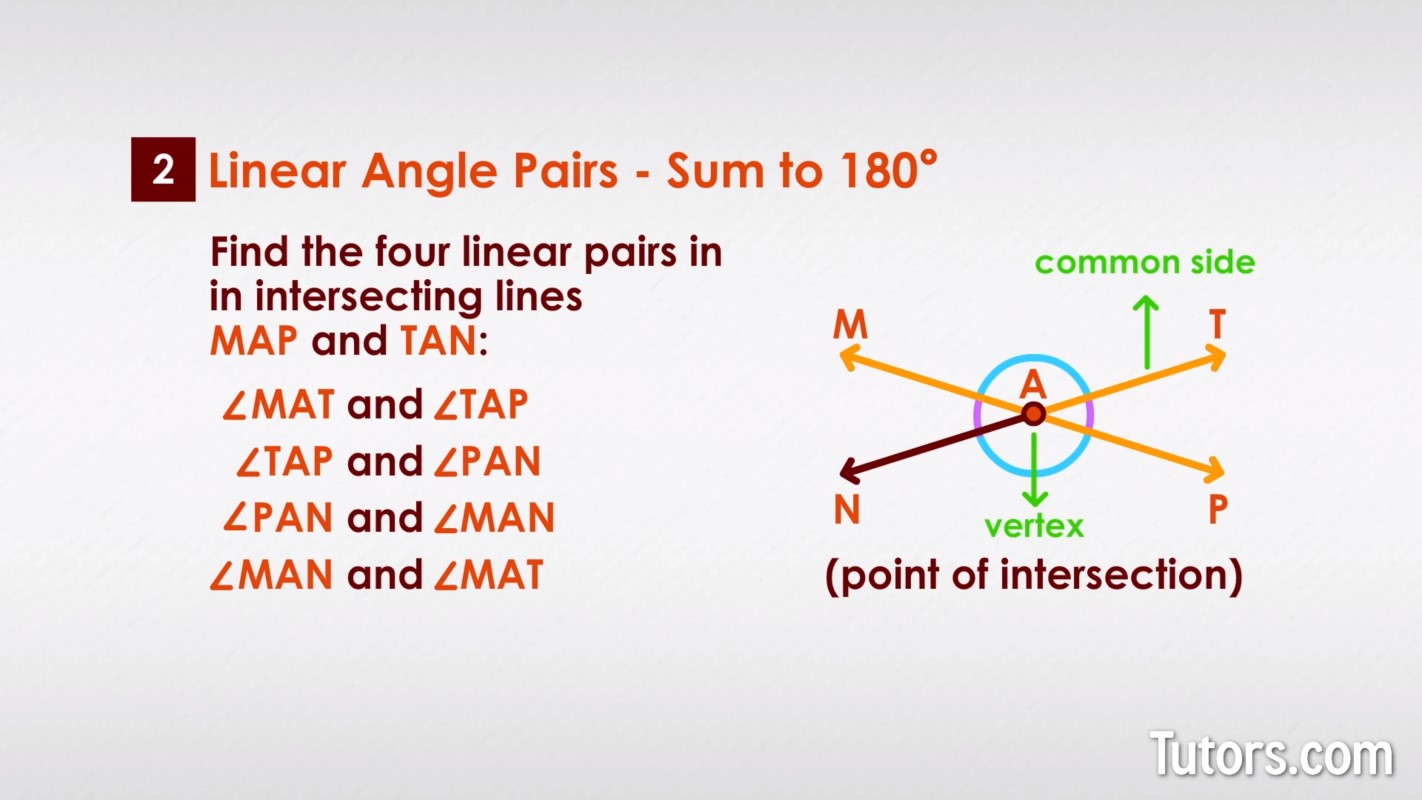
Did you find all these?

1. ∠MAT and ∠TAP
2. ∠TAP and ∠PAN
3. ∠PAN and ∠MAN
4. ∠MAN and ∠MAT

Supplementary angles need not be linear pairs. They just have to add to 180°. They do not have to share a common side. They do not have to be adjacent angles:

Congruent Angle Pairs

Two angle pairs are congruent (have the same measure):

1. Vertical angles
2. Right angles

Vertical angles share a vertex. When two lines intersect, two pairs of angles opposite each other are formed. These opposite angles are congruent. They are not adjacent angles because they do not share a common side.

Looking back at our intersecting lines above, we see that ∠MAN and ∠TAP share a common vertex, Point A, but do not share a common side. They are vertical angles and are congruent. The same is true of ∠MAT and ∠PAN.

Right angles will always be congruent, and any two right angles form complementary angle pairs.

Special Pairs

Some figures, such as parallel lines cut by a transversal, create special angle pairs:

• Alternate Interior Angles -- Angles on opposite sides of a transversal but between the two parallel lines form supplementary angle pairs
• Alternate Exterior Angles -- Angles on opposite sides of a transversal but outside the two parallel lines form supplementary angle pairs
• Corresponding Angles -- Angles in the same relative position at each intersection are congruent, shown with the symbol ≅

Here is a transversal, SD, cutting across parallel lines MH and EO at Points A and U. Yes, it is a MADHOUSE, but can you make sense of it?

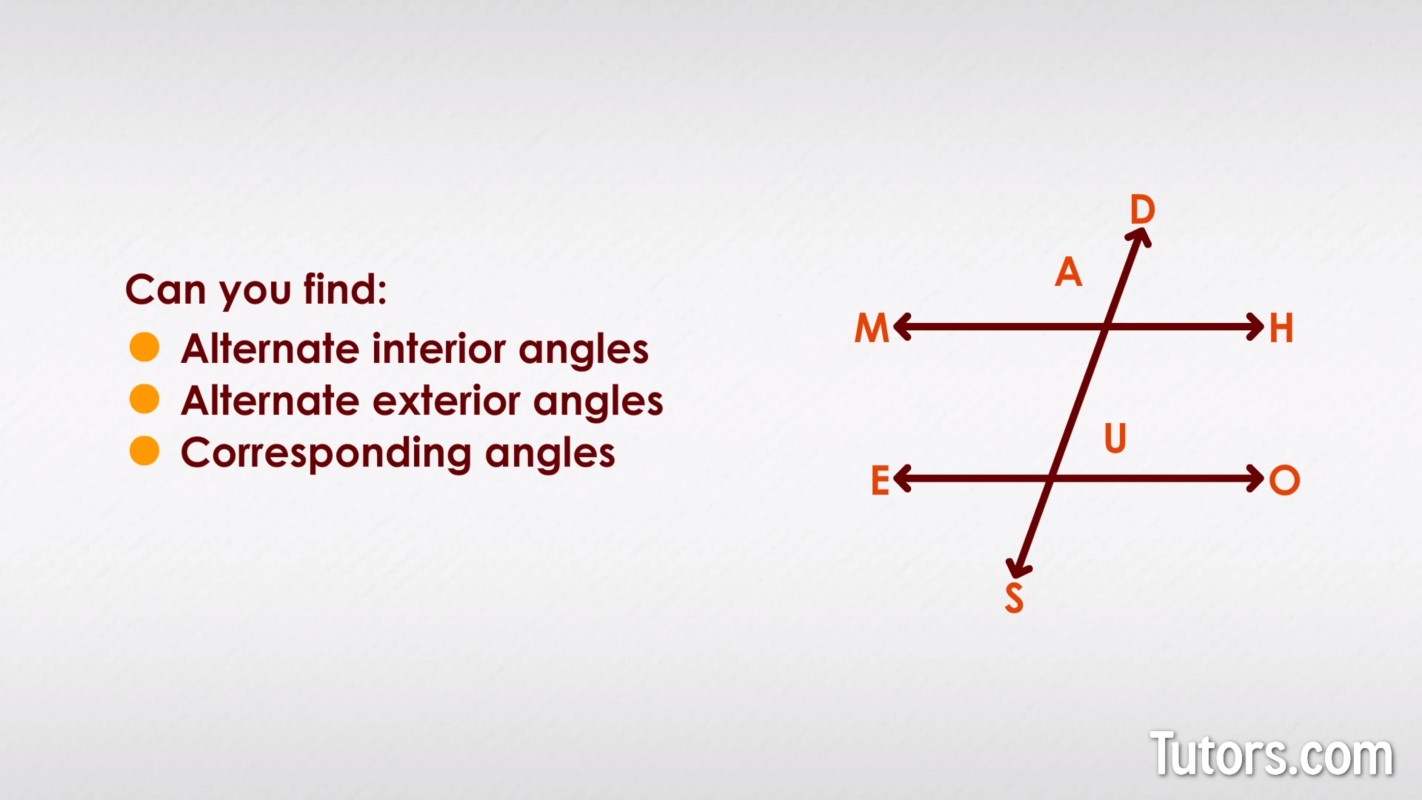
Can you find the alternate interior angles, alternate exterior angles, and corresponding angles?

• Alternate Interior Angles -- ∠MAU and ∠OUA; ∠HAU and ∠EUA
• Alternate Exterior Angles -- ∠MAD and ∠OUS; ∠HAD and ∠SUE
• Corresponding Angles -- ∠MAD ≅ ∠EUA; ∠HAD ≅ ∠OUA; ∠OUS ≅ ∠UAH; ∠MAU ≅ ∠SUE

Not-So-Special Pairs

Adjacent angles are often considered angle pairs, even though they have only one identifying property: they share a common vertex and side. They do not need to be complementary, supplementary, or special in any way.

Next Lesson:

Supplementary Angles