Exterior Angle Theorem — Formula & Examples
Exterior angle theorem
The exterior angle theorem tells us that any exterior angle of a triangle equals the sum of the opposite two interior angles and that the sum of all three interior angles of a triangle equals 180°, the sum of two right angles (triangle sum theorem).
Exterior angle theorem formula
The exterior angle theorem is based on Euclid’s proposition 16 and proposition 32 of his “Elements.” Together they give us the exterior angle theorem that we can use to solve missing angle measurements of triangles.
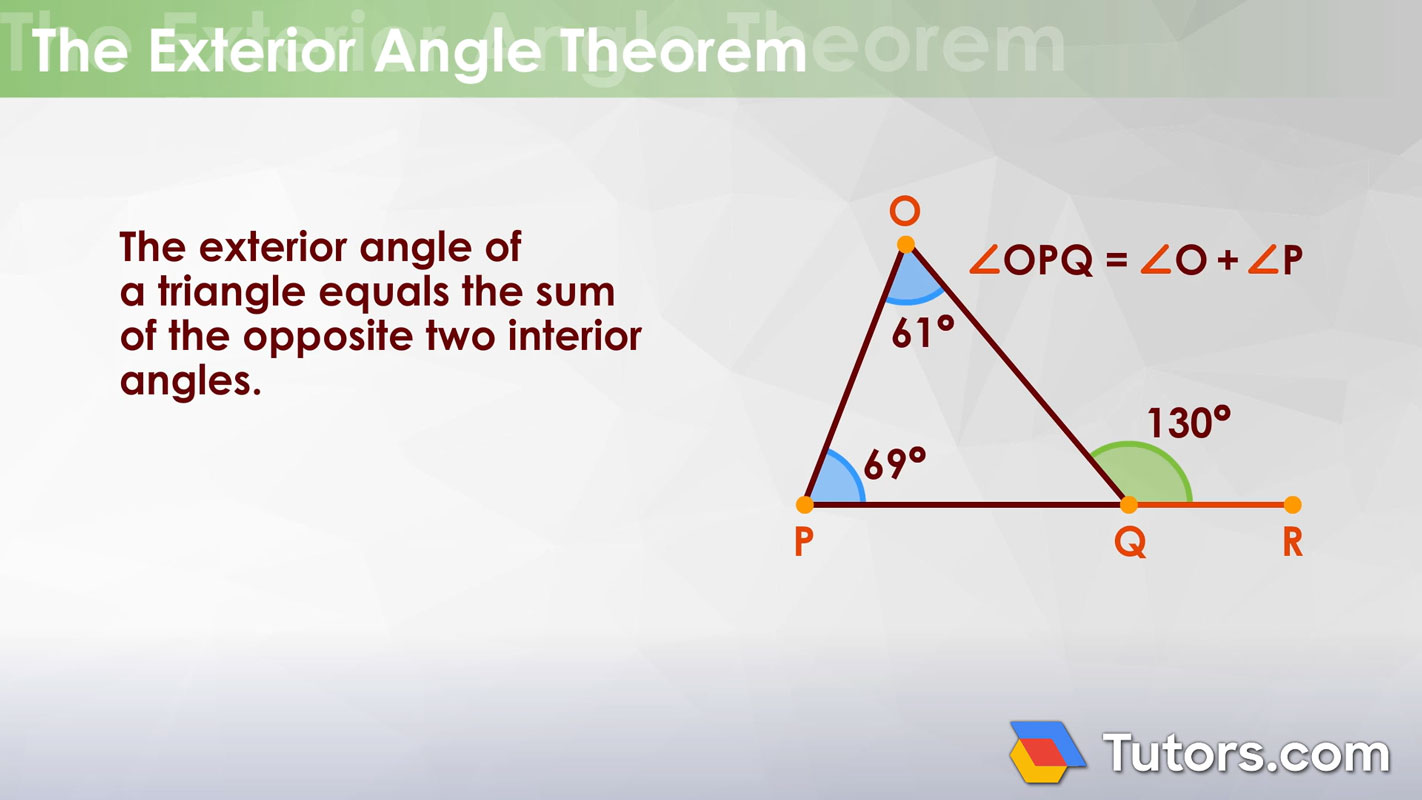
Exterior angles of a triangle
To understand the exterior angle theorem, you must know what an exterior angle of any polygon is. A triangle has three interior angles, but it also has six exterior angles, which are the angles between a side of a triangle and an extension of an adjacent side.
Taking one exterior angle at each vertex, the sum of any polygon’s exterior three angles is always 360°. This works in either direction.
Exterior angle theorem proof
Let's construct a triangle with an exterior angle and prove the exterior angle theorem.
Here is △ABC, named for it's three angles, angle A, angle B, and angle C. We have extended one side, BC, far past the triangle:
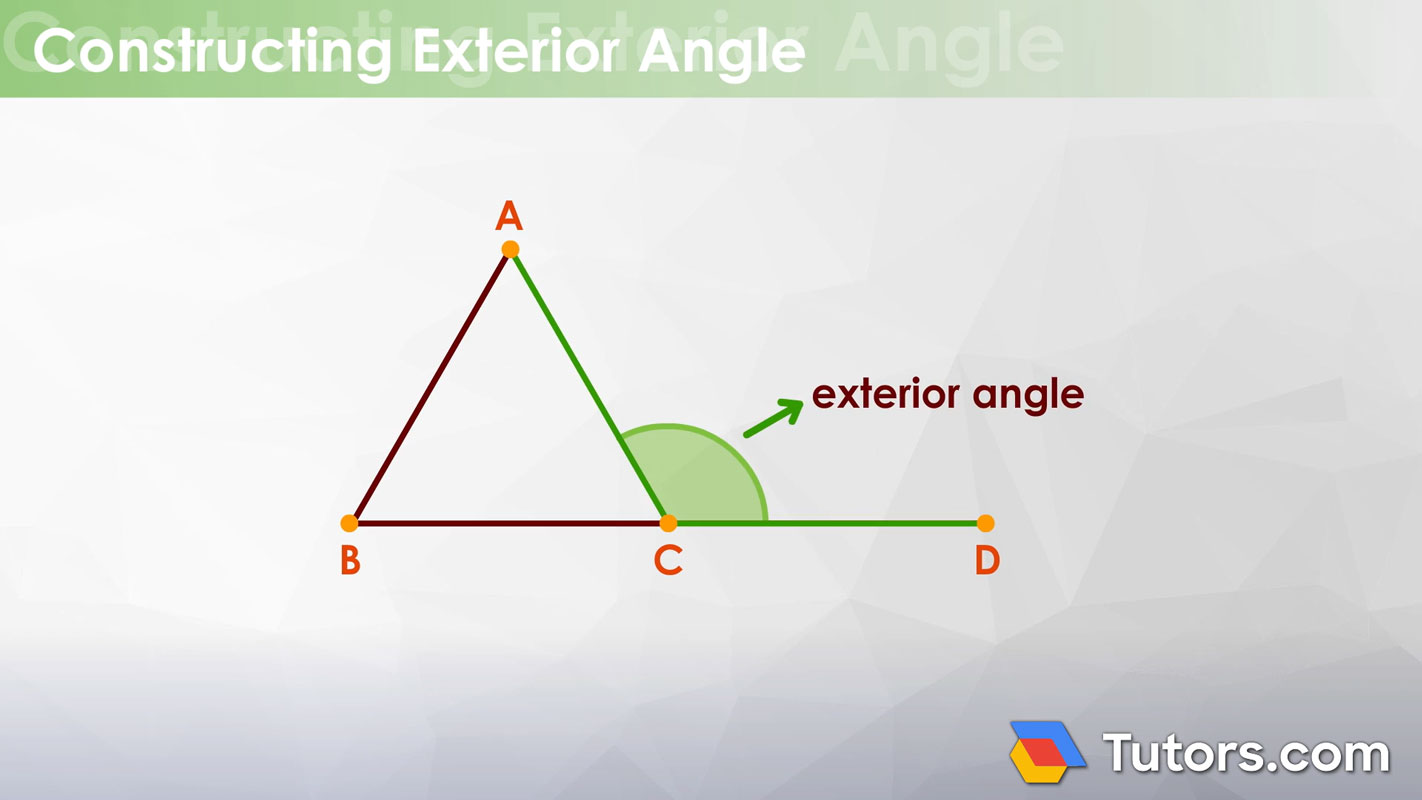
We add Point D on segment BC and now have segment BD. This gives us the exterior ∠ACD.
Next, we construct a line segment parallel to segment AB:
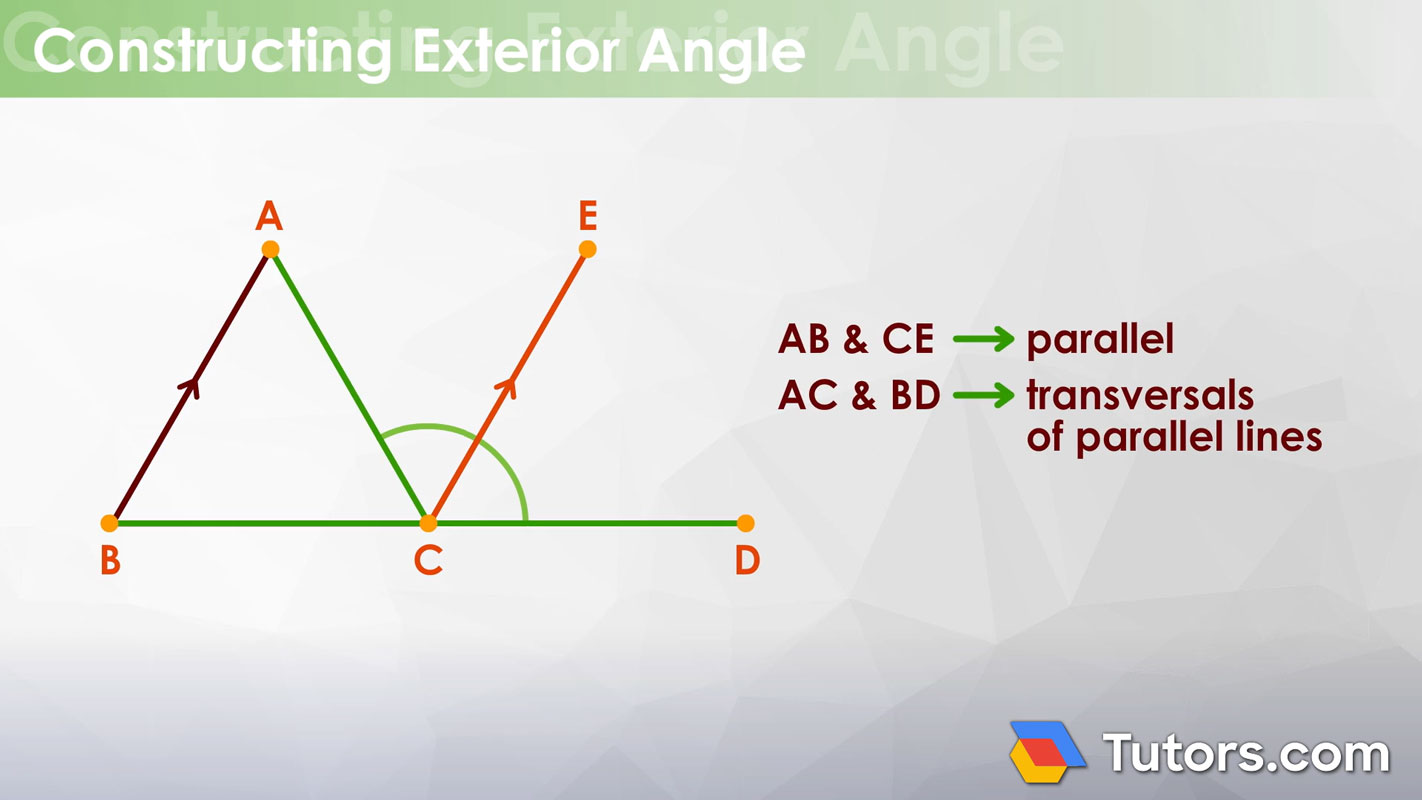
Since segments AB and CE are parallel, both line segments AC and BD are transversals of parallel lines. That means ∠BAC and ∠ACE are congruent because they are alternate interior angles of two parallel lines cut by a transversal.
The two angles, ∠ECD and ∠ABC, are also congruent because they are corresponding angles.
Therefore, ∠ACD is equal to the sum of the measures for ∠BAC + ∠ABC, the triangle’s two interior angles opposite the exterior ∠ACD.
The last step, adding interior ∠ACB to ∠ACD to get the straight line segment BD, demonstrates that the three interior angles of the triangle sum to 180°.
Exterior angle theorem example
The exterior angle theorem is useful for finding an unknown angle of any triangle. If you are given the measure of one exterior angle of the triangle, J, and one opposite angle, F, subtraction will give you the missing angle, G. The symbol, ∠ indicates a measured angle.
Subtract the known interior angle from the exterior angle:
Suppose an exterior angle measures 110° and you are told one of its opposite interior angles measures 47°. Plug in the knowns to find the unknown:
Now you know two of the three interior angles and can, if needed, easily find the third interior angle by subtracting them from 180°:
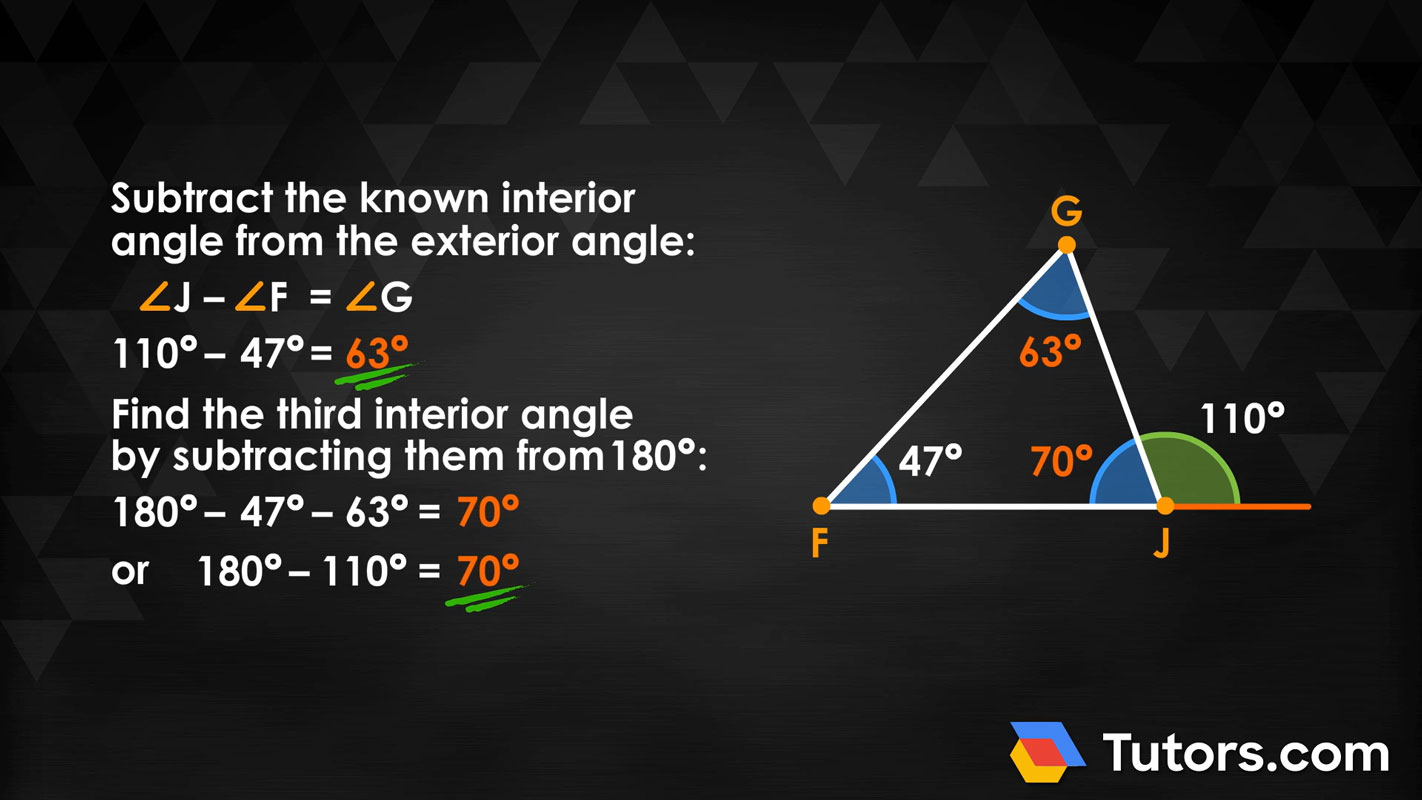
You can also use the theorem to find the angle adjacent to the exterior angle, simply by subtracting the exterior angle from 180°.
Exterior angle theorem FAQ
Do you have this figured out? Check for understanding by answering these questions.
How many exterior angles does a triangle have? How many interior angles?
What is the sum of the interior angles of a triangle?
What is the sum of one set of exterior angles of a triangle?
An exterior angle of a triangle measures 145° and one of its opposite interior angles is 51°. What is the measure of the other opposite interior angle?
An exterior angle of a triangle measures 139°. What is the measure of the triangle’s adjacent interior angle?
Please do your best before checking your answers against ours.
A triangle has six exterior angles and three interior angles.
The sum of the interior angles of a triangle is 180° (triangle sum theorem).
The sum of one set of exterior angles of a triangle is 360°.
An exterior angle of a triangle measures 145° and one of its opposite interior angles is 151°. The measure of the other opposite interior angle is 91°
An exterior angle of a triangle measures 139°. The measure of the triangle’s adjacent interior angle must be 41°. They are supplementary angles.