Interior and Exterior Angles of Triangles — Definition & Examples
Interior angles of a triangle
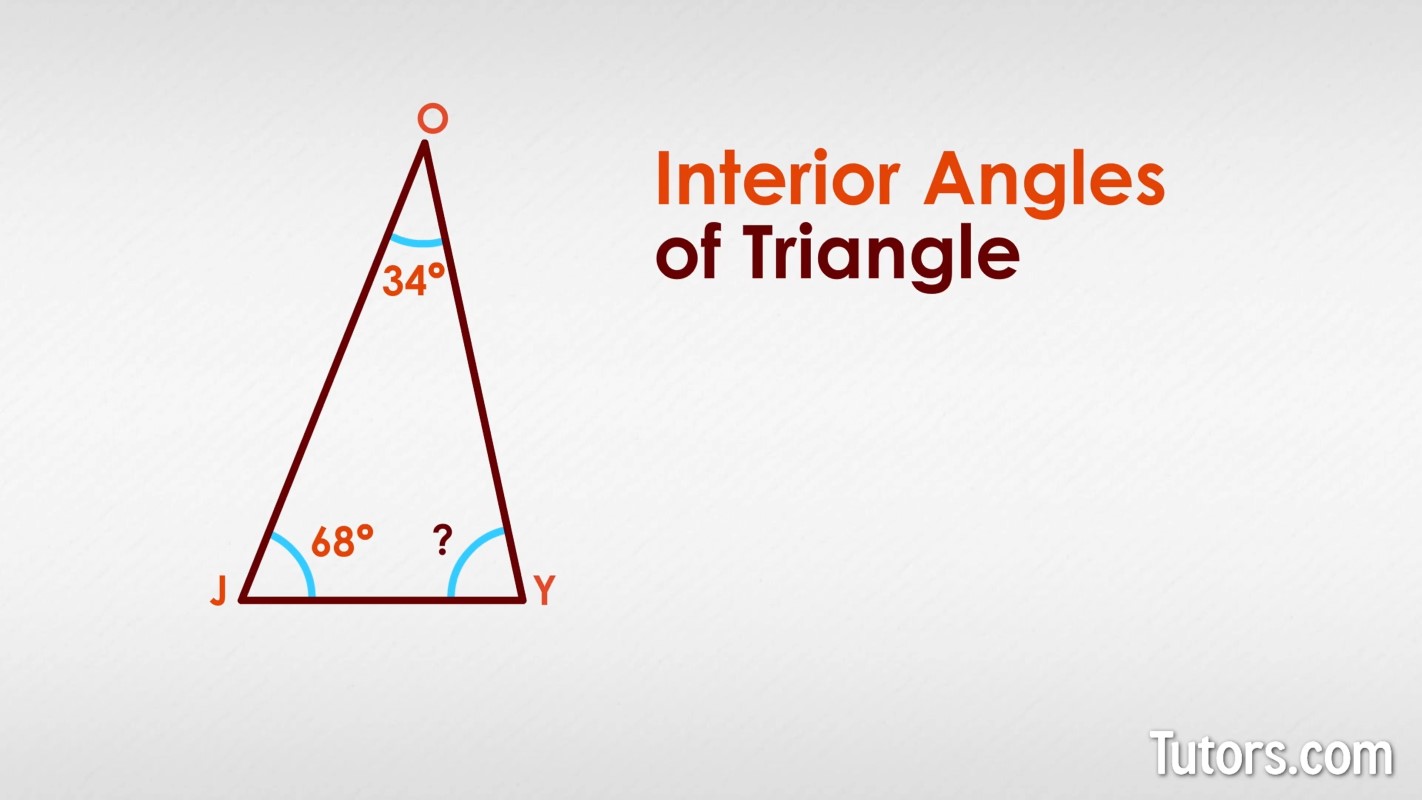
Interior angles of a triangle are the three angles created at the vertices, or corners, of the triangle on the inside. A triangle stakes out a space, its area, inside its sides. Here is , with sides JO, OY, and YJ making up the three interior angles:
JO and OY make
OY and YJ make
JO and YJ (or JY)
make
Notice we have labeled measuring 68° and measuring 34°. The three interior angles of a triangle must add to 180°. With that clue, can you calculate ? If not, fear not! You will learn how a little later.
Exterior angles of a triangle
Before we delve any further into exterior angles of a triangle, know this one fact:
Consider strolling around the shape. If you were to walk around a triangle laid out on the ground, you would make one complete turn, 360°, of your body.
No matter the triangle, you would start off facing one direction, walk around, and return to the same spot in the same direction after turning your body completely around.
Supplementary angles
An exterior angle is the supplement, or amount needed to sum to 180°, to a triangle's interior angle. Supplementary angles are angles that add to make a straight angle or straight line, 180°. Here is with measuring 73°.

That is made with sides LA and LF. If we extended side LF past side LA as a straight line, the angle from side LA over to the extension sums to 180°. It has to be 107°:
Triangle exterior angle theorem
Many geometry students wonder why the exterior angles of a triangle do not take in the entire sweep of the outside of the triangle from one side to the next. Such a big angle is called a reflex angle (greater than 180° but less than 360°).
The definition of an exterior angle relates that angle to the two opposite interior angles.
If the exterior angle were greater than supplementary (if it were a reflex angle), the theorem would not work. Every exterior angle would be the reflex to the adjacent interior angle, with unpredictable results. Another theorem tells you that the exterior angle of a triangle is always greater than either opposite angle. This can be handy in checking your subtraction. If you subtract an interior angle from 180° and get a number that is equal to or smaller than either of the other two interior angles, you did something wrong. Check your work!
Both of these theorems are straight out of Euclid's Elements. He states that "something more" as:
Calculating unknown interior angles of a triangle
Look back at , where we have two known interior angles. To know all three interior angles of a triangle, we subtract angles we know from 180°:
Our unknown must be 78°.
Calculating unknown exterior angles of a triangle
We'll stick with to explore exterior angles of a triangle. We know all three interior angles, so to calculate each exterior angle, we subtract each interior angle from 180°.
= 68°, subtract 68° from 180° to get 112°
= 34°, subtract 34° from 180° to get 146°
= 78°, subtract 78° from 180° to get 102°
Check to see if the exterior angles add to 360°.
You can use the two theorems to calculate any exterior angle if you can figure out the interior angle. You can use your knowledge of the sum of interior angles to calculate unknown interior angles of a triangle.
Try it!
Imagine or draw , and all you know is that it has one right angle, , and that . Have some fun with and find all this:
Exterior angle to
Exterior angle to
Exterior angle to
Stumped? Use your knowledge of the sum of interior angles to find :
Now use your knowledge of exterior angles of triangles to calculate each exterior angle:
Exterior angle to
Exterior angle to
Exterior angle to
Lesson Summary
Now that you have reviewed the instructions and studied the multimedia, you are able to define, locate and identify interior angles of a triangle and the exterior angles of triangles. You can now recall and apply the Triangle Exterior Angle Theorem, and use properties of angles and triangles to calculate unknown interior angles and exterior angles.