What is a Square? (Definition & Properties)

Square definition

A square is a four-sided figure whose sides are all the same length and whose angles are all right angles measuring 90 degrees. To be a square, a shape must be all these things:

• A plane figure

• A closed shape

• A regular polygon

• A quadrilateral

Behold the square. It may seem a little boring at first, but once you find out more about a square, you will see it is intriguing and very useful. Squares appear all around you. They are great for building, decorating, and making three-dimensional shapes. And, believe it or not, squares have a lot of interesting identifying properties.

What is a square?

The family of quadrilaterals includes many shapes, and a square can be some of them. A square is a type of parallelogram, rectangle, and rhombus. It is a parallelogram because it has two pairs of parallel, congruent sides. It is a rectangle because it has two pairs of parallel, congruent sides with four congruent interior angles. It is a rhombus because it has four congruent sides.

All squares are parallelograms, rectangles and rhombi, but not all parallelograms, rectangles and rhombi are squares.

A square is a regular polygon because it has equal-length sides (equilateral) and equal-measure angles (equiangular). Compare it to the regular polygon with only three sides, the equilateral triangle, or an regular octagon as you can see in stop signs at street intersections.

How to construct a square

You can construct a square using four straight (linear) objects of equal length. Lay down your four straight objects (pens, rulers, shoelaces) so all eight endpoints touch exactly one other endpoint. Work with the objects until all four interior angles appear to be the same.

You have constructed a square, because the four sides are equal (equilateral) and the four interior angles are equal (equiangular). Each interior angle is 90°.

How to draw a square

You can draw a square using a ruler, pencil, and protractor. Draw a horizontal line segment on a piece of paper, near the paper's center. Label it YN, so endpoint Y is to your left and endpoint N is at the right.

Use your protractor to draw a line segment rising up from endpoint Y, perpendicular to line segment YN and the same length as YN. Label its endpoint Z.

Repeat that process to make a line segment rising up from endpoint N. Label its endpoint A.

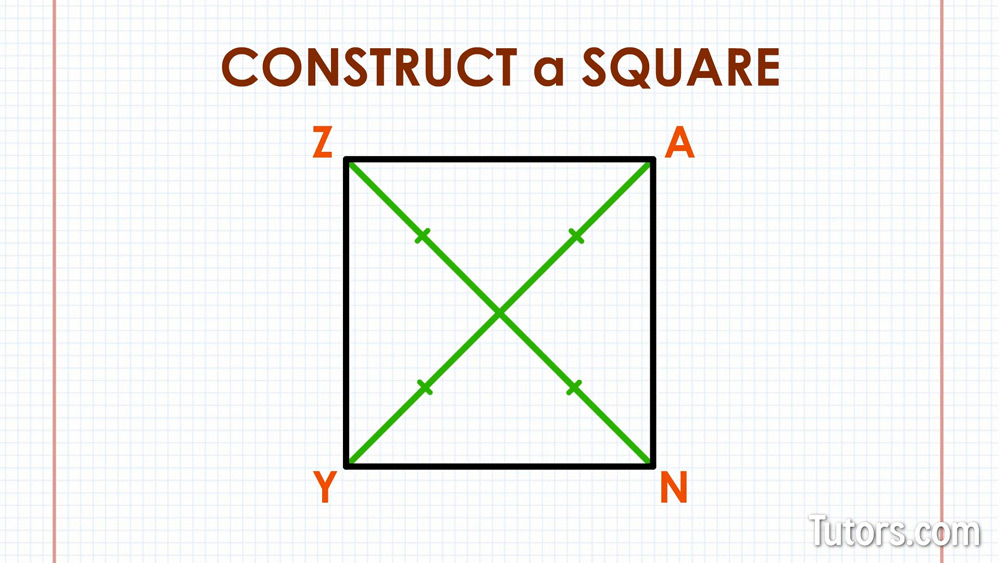
If you drew everything correctly, connecting endpoint Z to endpoint A gives you a square, ZANY.

If you connect endpoints Z and N, you have a diagonal of the square. Connect A and Y and you have the other diagonal.

Squares in real life

The square is an easy shape to make, cut, or build out of everyday materials. It also can cover a plane when you repeatedly put squares against each other.

When you cover a surface so nothing peeks out, you tessellate the surface. Only a few regular polygons can tessellate a surface, and a square is one of them. This makes a square very handy for building, decorating, and producing art. You can find squares everywhere.

Many floor tiles and ceiling panels are squares. Ceramic bathroom tiles are often squares. Artists and architects use squares a lot.

The base of a square pyramid, a three-dimensional solid, is a square. The faces of cubes and dice (also three-dimensional or 3D solids) are squares.

You can find squares in pictures, picture frames, crossword puzzle boxes, the sides of little children's building blocks, Scrabble tiles and the Scrabble board, and even the keys on many computer keyboards.

In the United States, most paper for writing and printing is rectangular, not square, but in Japan square paper is used for folding in the art of origami. You can make wonderful animals and other figures in origami, all starting with a square of paper.

Properties of a square

Squares have three identifying properties related to their diagonals, sides, and interior angles.

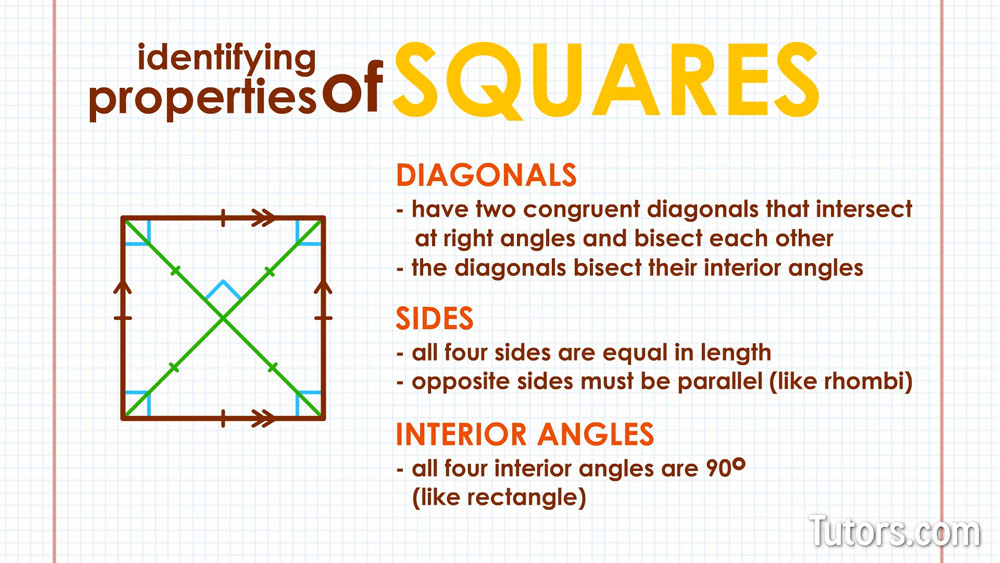
Diagonals

All squares have exactly two congruent diagonals that intersect at right angles and bisect (halve) each other. The diagonals of a square also bisect their interior angles.

Sides

All four sides of a square are congruent. That means they are equal to each other in length. To be congruent, opposite sides of a square must be parallel. The rhombus shares this identifying property, so squares are rhombi.

Interior angles

All four interior angles of a square are congruent. Since interior angles of any quadrilateral must add to 360°, some quick division shows you that each angle is 90°.

All squares, therefore, have four right angles. The rectangle shares this identifying property, so squares are rectangles.

How to find the perimeter of a square

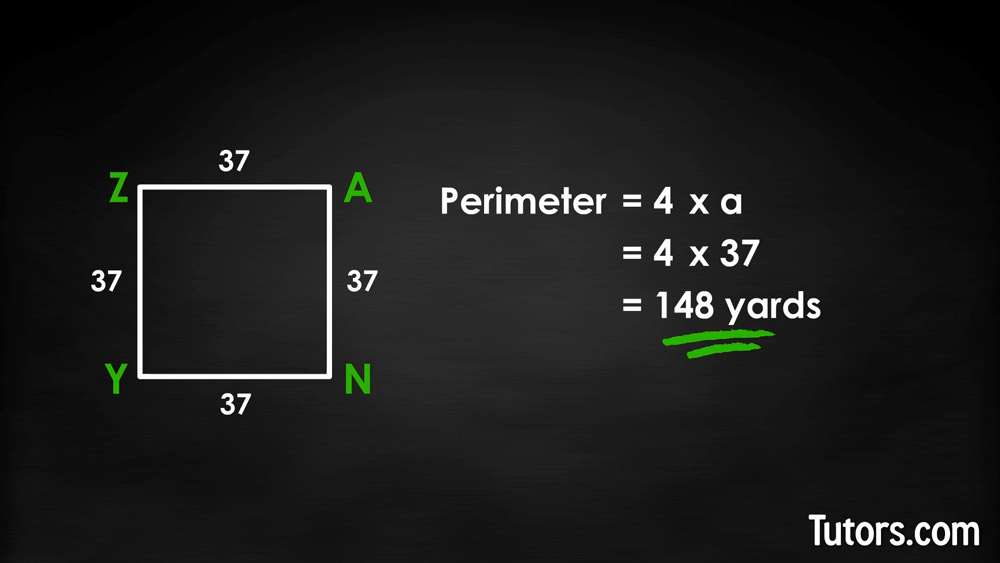
Because a square has four congruent (equilateral or equal-length) sides, finding the distance around the shape is very easy. Label the length of any side a, and then multiply times 4:

Formula for perimeter of a square

So for our square ZANY, one of the sides is 37 yards.

Example #2

Try it yourself. Let's say square ZANY has one side of 1,000 meters. What is the perimeter?

How to find the area of a square

Area is always expressed in square units of the linear measurement. Normally we say area is equal to length times width, but in a square, the length is the width. This makes your work easier.

To find the area of a square, multiply the length of any side times itself (raise it to the second power):

Formula for area of a square

Let's find the area of a square with a side of 37 yards.

Example #3

Try it yourself. Take our same square ZANY with sides of 1,000 meters. What is its area in square meters?

Lesson summary

By watching the video and reading these instructions, you have learned all about the geometric figure, the square. You know how to construct a square. You can identify squares all around you, you can tell how a square fits into the family of quadrilaterals, and you can spot the three identifying properties of a square.

You can calculate the perimeter and area of a square using the formulas $P=a\times 4$P=a×4 where a is the length of one side and $A={a}^{2}$A=a2, in square units.