What is a Rhombus? (Definition, Shape, Properties)
Rhombus definition
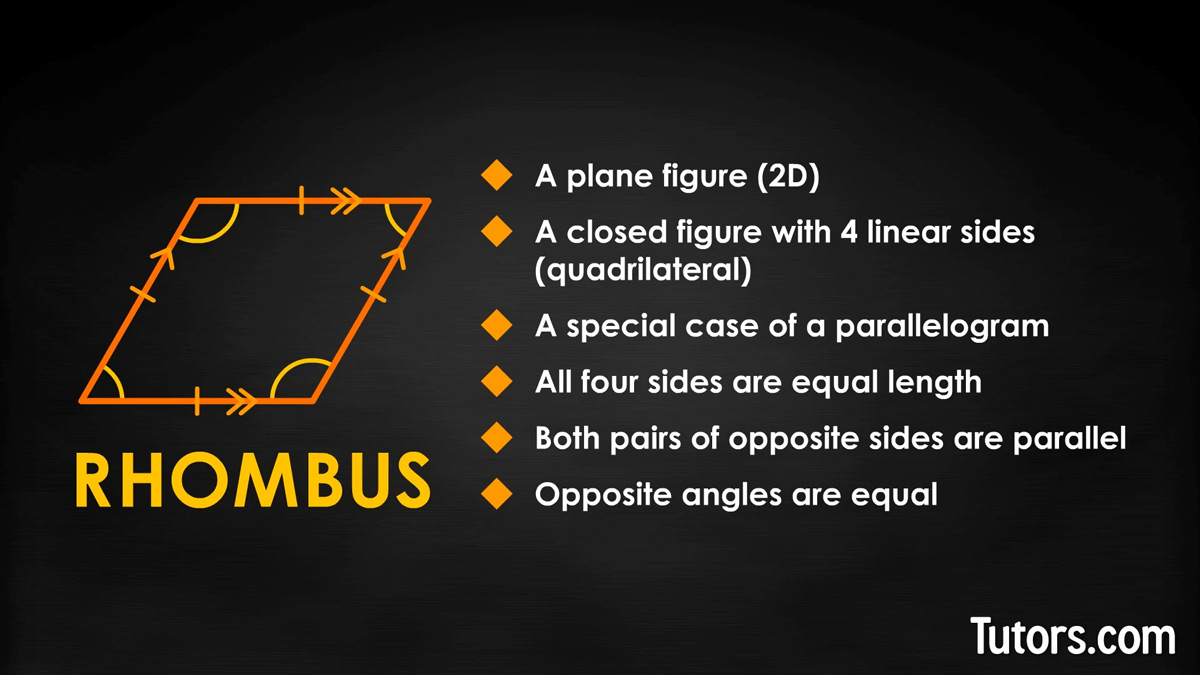
A rhombus is a quadrilateral with four equal-length sides and opposite sides parallel to each other. All rhombuses are parallelograms, but not all parallelograms are rhombuses. The opposite interior angles of rhombuses are congruent and the diagonals of a rhombus always bisect each other at right angles.
Rhombus shape
Every rhombus is:
A plane figure (it has two dimensions)
A closed shape (it has an interior and exterior)
A quadrilateral (four-sided plane figure with straight sides)
What does a rhombus look like?
Most times, the rhombus you see will be drawn so it has a base -- two opposite sides will be horizontal, with the bottom side serving as the shape's base.

Be careful, though, because a rhombus can appear at any orientation. When it "stands up" so it is symmetrical in appearance, (its diagonals are horizontal and vertical) it is usually called a diamond.
If you struggle to remember its name, think of a square that has been run into by a bus, so it is tilted over (run into by a bus … rhombus).
Is a square a rhombus?
All squares are rhombuses, but not all rhombuses are squares. If you have a rhombus with four equal interior angles, you have a square.
A square is a special case of a rhombus, because it has four equal-length sides and goes above and beyond that to also have four right angles.
Is a rhombus always a parallelogram?
A rhombus is a special case of a parallelogram, because it fulfills the requirements of a parallelogram: a quadrilateral with two pairs of parallel sides. It goes above and beyond that to also have four equal-length sides, but it is still a type of parallelogram.

Are rhombuses quadrilaterals?
If you have a quadrilateral with only one pair of parallel sides, you definitely do not have a rhombus (because two of its sides cannot be the same length). You have a trapezoid.
If you have a quadrilateral with two pairs of parallel sides, you do not necessarily have a rhombus; you might have a parallelogram, or you could have a rhombus if all four sides are the same length.
Properties of a rhombus
One of the two characteristics that make a rhombus unique is that its four sides are equal in length, or congruent. The other identifying property is that opposite sides are parallel.

Rhombus angles
In addition to those four sides, the rhombus has four interior angles. You can also construct two diagonals inside the rhombus by connecting opposite vertices (corners).

No matter how you arrange those four linear objects on your flat surface, you will always have two pairs of equal opposite angles.
Start over with two of your objects and this time, concentrate on making an acute (less than 90°) angle out of them. Use the other two objects to connect the original two, up and to the right, to make your four-sided (quadrilateral), plane figure - a rhombus.
Look at the bottom left angle and the top right angle; they are the same. They are congruent. Look at the bottom right angle and the top left angle: they are congruent. Opposite interior angles of a rhombus are congruent.
Diagonals of a rhombus
A wonderful and rare property of a rhombus is that its diagonals are always perpendicular to each other. No matter what angles you have for the rhombus's four vertices, the diagonals of a rhombus are always at right angles to each other.
These diagonals also cut each other exactly in half. Geometricians say they bisect each other. That means the two diagonals divide the rhombus up into four right-angle triangles.
Different names for a rhombus
A rhombus can have three additional names:
Rhomb
Lozenge
Diamond
How to construct a rhombus
You can build a rhombus right now, on any flat surface, if you have four identical, linear objects. Toothpicks, pencils, meter sticks -- any four congruent, straight line segments will do.
Lay the four straight objects out on the flat surface so their eight ends touch in only four places. You cannot fail at this! Lay two objects down to be parallel to each other but a slight distance apart. If you use the other two objects to connect end points, you have a rhombus!