20+ tutors near you & online ready to help.

TABLE OF CONTENTS

Pythagorean Theorem

Written by

Malcolm McKinsey

January 16, 2023

Fact-checked by

Paul Mazzola

What is the Pythagorean theorem?

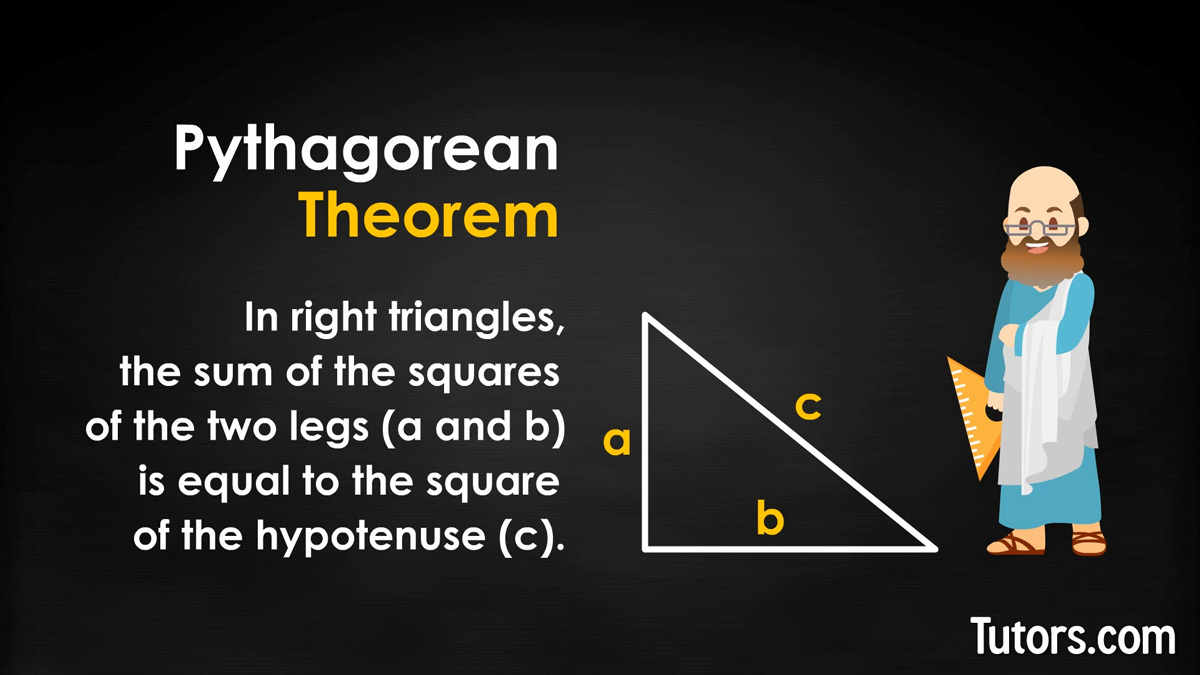
The Pythagorean theorem states that in right triangles, the sum of the squares of the two legs (a and b) is equal to the square of the hypotenuse (c).

The Pythagorean Theorem is a very handy way to find the length of any one side of a right triangle if you know the length of the other two sides.

Pythagorean theorem history

The Pythagorean Theorem is named after and written by the Greek mathematician, Pythagoras. Pythagoras is pronounced ("pi-thag-uh-rus," with a short "I" sound in his first syllable; pi as in pin), but the theorem has been described in many civilizations worldwide. The theorem is pronounced "pi-thag-uh-ree-uhn."

A theorem in geometry is a provable statement. The Pythagorean Theorem was proven very long ago.

Get free estimates from geometry tutors near you.

Pythagorean theorem formula

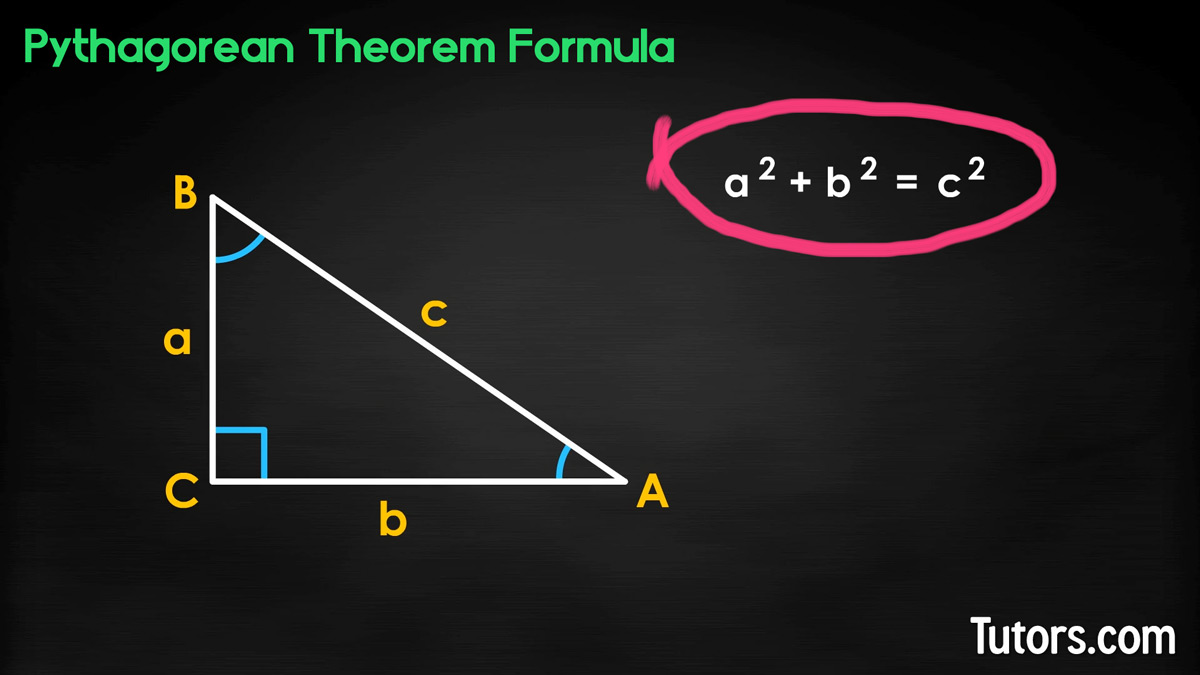
In any right triangle ABC, the longest side is the hypotenuse, usually labeled c and opposite ∠C. The two legs, aa and bb, are opposite ∠A and ∠B. ∠C is a right angle, 90°, and ∠A + ∠B = 90° (complementary).

The three sides always maintain a relationship such that the sum of the squares of the legs is equal to the square of the hypotenuse. In mathematics terms it looks like this:

{a}^{2}+{b}^{2}={c}^{2}

How to use the Pythagorean theorem

The Pythagorean Theorem can be used to find the length of the hypotenuse if you know the lengths of legs a and b.

Solve for c

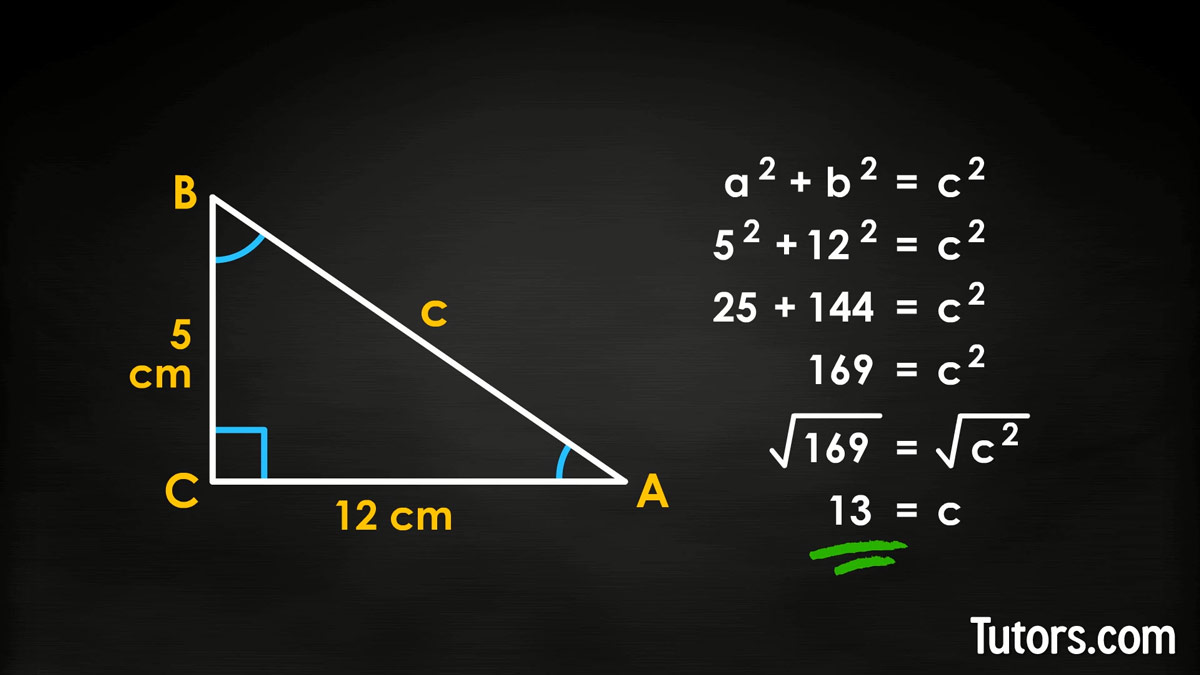
Suppose you have leg a=5 centimeters and b=12 centimeters:

Pythagorean theorem steps explained

We start with our formula ${a}^{2}+{b}^{2}={c}^{2}$ , then we plug in the length of each leg:

{5}^{2}+{12}^{2}={c}^{2}

Next, multiply each number times itself:

25+144={c}^{2}

Then we add:

169={c}^{2}

Now, we take the square root of both sides:

\sqrt{169}=\sqrt{{c}^{2}}

So you take the principal root of both sides and you get:

13=c

Solve for a or b

You can know the length of the hypotenuse and one leg and still use the Pythagorean Theorem. Suppose you know c=40 feet and short leg a=24 feet.

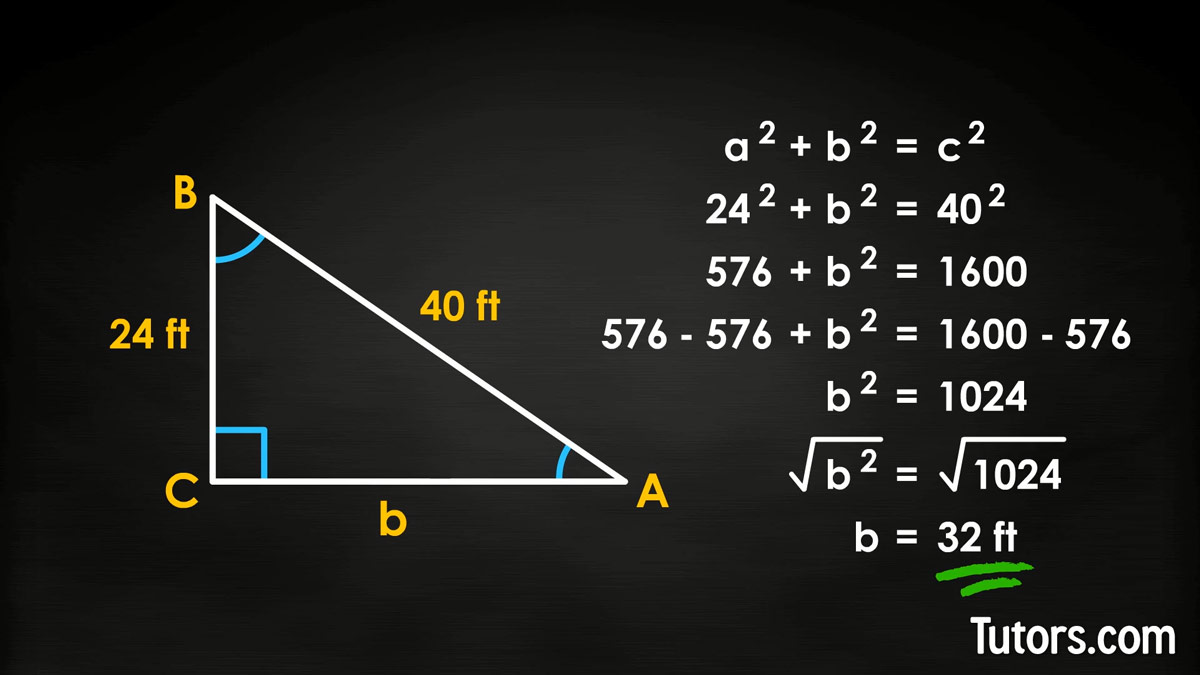
Step by step

First, plug what you know into our formula:

{24}^{2}+{b}^{2}={40}^{2}

Multiply each number times itself, then add:

576+{b}^{2}=1,600

Then, you need to subtract the ${a}^{2}$ length from both sides, to isolate ${b}^{2}$ :

(576-576)+{b}^{2}=(1600-576)

On the left handed side we're left with just

{b}^{2}

{b}^{2}=1,024

Now take the square root of both sides:

\sqrt{{b}^{2}}=\sqrt{1024}

Take the principal root of both sides and you get:

b=32

You can use the Pythagorean Theorem to solve for any length if you know the lengths of two other sides.

Checking your answer

So our right triangle had legs a=24, b=32, and hypotenuse c=40. If you do not believe your answer, plug all three numbers back into the Pythagorean Theorem:

{24}^{2}+{32}^{2}={40}^{2}

Let's check if the numbers add up:

576+1024=1600

Everything checks out; we were right! And our numbers were nice, whole integers, which made the work easy.

Pythagorean theorem with square roots

Suppose you need the length of the hypotenuse c. Then you simply need the square root of the sum of a2+b2, like this:

c=\sqrt{{a}^{2}+{b}^{2}}

If you need to find the short leg a, manipulate the formula to look like this:

a=\sqrt{{c}^{2}+{b}^{2}}

And if you need to find the longer leg b, you rewrite the formula to look like this:

Get free estimates from geometry tutors near you.

b=\sqrt{{c}^{2}+{a}^{2}}

Pythagorean theorem word problems

An firefighter's extension ladder is leaning against a building, so its top just touches the gutters at the roof edge. You know the ladder is 41 feet long and it is 9 feet from the wall of the building. How high is the building?

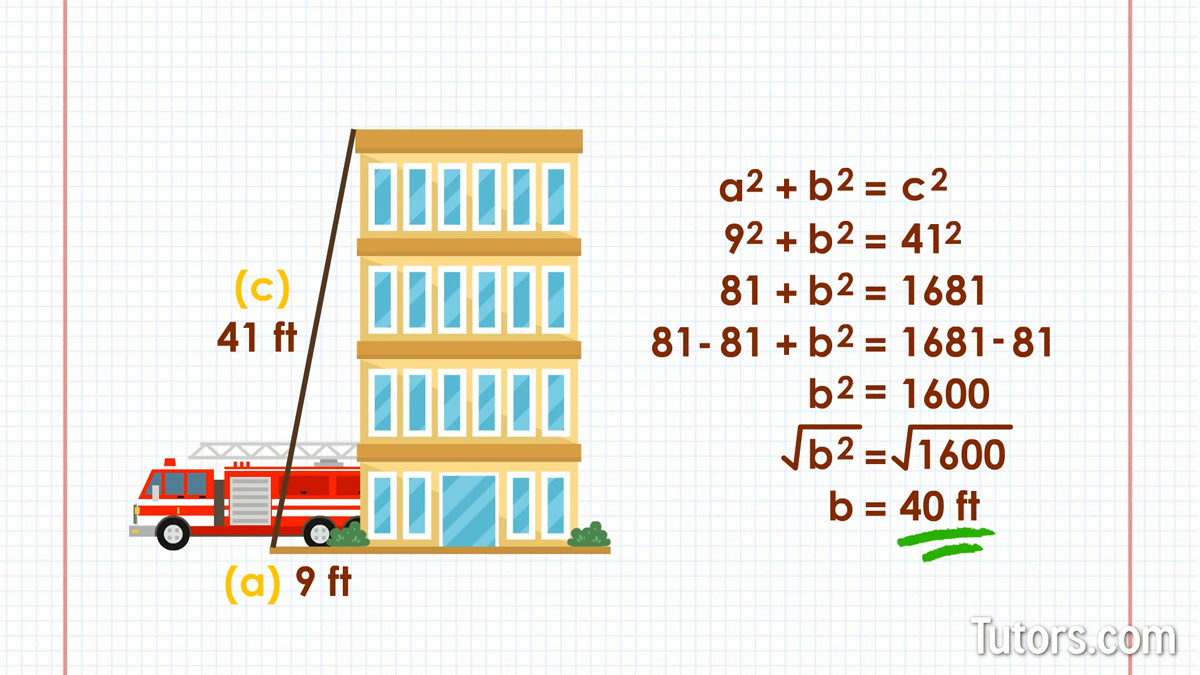
The ladder is the hypotenuse, 41', and leg aa is the short leg, 9'. Plug in what you know into either formula you wish to use to solve for long leg b:

Start with our formula and plug in what you know:

{9}^{2}+{b}^{2}={41}^{2}

Multiply each number times itself, then add:

81+{b}^{2}=1681

Then, you need to subtract the ${a}^{2}$ length from both sides, to isolate ${b}^{2}$ :

(81-81)+{b}^{2}=(1681-81)

On the left handed side we're left with just ${b}^{2}$ .

{b}^{2}=1,600

Now take the square root of both sides:

\sqrt{{b}^{2}}=\sqrt{1600}

Take the principal root of both sides and you get:

b=40

Let's solve this another way!

If you need to find the longer leg b, you rewrite the formula to look like this:

b=\sqrt{{c}^{2}-{a}^{2}}

b=\sqrt{{41}^{2}-{9}^{2}}

b=\sqrt{1681-81}

b=\sqrt{1,600}

b=40

Pythagorean theorem examples

Find the answers to these five Pythagorean Theorem problems:

Example #1

Find the hypotenuse c for a right triangle with the length of short leg a=6 and the length of the long leg b=8:

{a}^{2}+{b}^{2}={c}^{2}

{6}^{2}+{8}^{2}={c}^{2}

36+64={c}^{2}

100={c}^{2}

\sqrt{100}=\sqrt{{c}^{2}}

10=c

Example #2

Find the short leg a for a right triangle with the length of long leg b=24 and the length of the hypotenuse c=25:

{a}^{2}+{24}^{2}={25}^{2}

{a}^{2}+576=625

{a}^{2}+(576-576)=(625-576)

{a}^{2}=49

\sqrt{{a}^{2}}=\sqrt{49}

a=7

Example #3

Find the long leg b for a right triangle with the length of short leg a=65 and the length of the hypotenuse c=97:

{65}^{2}+{b}^{2}={97}^{2}

4,225+{b}^{2}=9,409

(4,225-4,225)+{b}^{2}=(9,409-4,225)

{b}^{2}=5,184

\sqrt{{b}^{2}}=\sqrt{5,184}

b=72

Example #4

Find the short leg a for a right triangle with the length of long leg b=60 and the length of the hypotenuse c=68:

a=\sqrt{{c}^{2}-{b}^{2}}

a=\sqrt{{68}^{2}-{60}^{2}}

a=\sqrt{(68+60)-(68-60)}

a=\sqrt{(128\times 8)}

a=\sqrt{{1024}^{2}}

a=32

Example #5

Find the long leg b for a right triangle with the length of short leg a=60 and the length of the hypotenuse c=100:

b=\sqrt{{c}^{2}-{a}^{2}}

b=\sqrt{{100}^{2}-{60}^{2}}

b=\sqrt{(100+60)(100-60)}

b=\sqrt{(160\times 40)}

Get free estimates from geometry tutors near you.

b=\sqrt{{6,400}^{2}}

b=80

Pythagorean triples

The reason our example problems ended up with nice, neat, whole numbers is because we used Pythagorean triples, or three whole numbers that work to fulfill the Pythagorean Theorem.

The smallest Pythagorean Triple is 3, 4, 5 (a right triangle with legs of 3 and 4 units, and a hypotenuse of 5 units). All the multiples of that triple will also be triples:

6, 8, 10
9, 12, 15
12, 16, 20

The list never ends, and includes one of our examples: 24, 32, 40.

Other Pythagorean Triples exist, too:

5, 12, 13 (we used that one in our example!)
8, 15, 17
9, 40, 41

That list never ends, either!

Learn how to identify and categorize Pythagorean triples as either primitive or imprimitive (not primitive) and learn how to use the Pythagorean theorem to find Pythagorean triples.

Pythagorean theorem proof

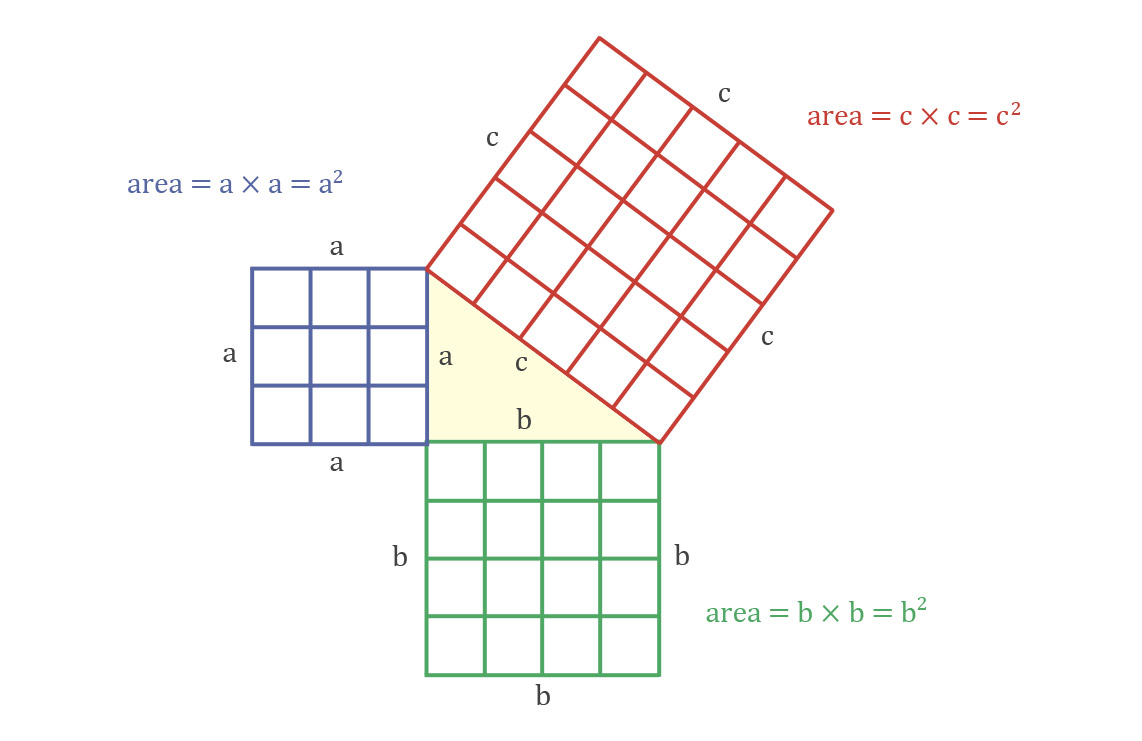
Thousands of proofs of this theorem exist, including one by U.S. president James Garfield (before he became president). One proof is easy to make with graph paper, a straightedge, pencil, and scissors.

Construct △ABC with legs a and b to the left and bottom and hypotenuse c at the top right. Leg a is opposite ∠A, leg b is opposite ∠B, and hypotenuse c is opposite right angle C.

Let length a=3, b=4, and hypotenuse c=5.

How to prove the Pythagorean theorem

Construct a square using leg aa as the right side of the square. It will be 9 square units ( ${a}^{2}$ ). Construct a square using leg b as the top side of its square, so it is 16 square units ( ${b}^{2}$ ). Cut out another 5 x 5 square and line it up with hypotenuse c, so the square is ${c}^{2}$ .

Think: what is 9 square units + 16 square units? It is 25 square units, the area of ${c}^{2}$ .

area=a\times a={a}^{2}

area=b\times b={b}^{2}

area=c\times c={c}^{2}

{a}^{2}+{b}^{2}={c}^{2}

Lesson summary

If you worked carefully, now you should know what the Pythagorean theorem is, recognize it when you see it, and apply it to solve problems in geometry. You can use it to find the length of any one side of a right triangle if you know the lengths of the other two sides. We also learned how to prove the Pythagorean theorem.