What is a Right Triangle

Written by

Malcolm McKinsey

January 20, 2023

Fact-checked by

Paul Mazzola

Right triangle definition

All triangles have interior angles adding to 180°. When one of those interior angles measures 90°, it is a right angle and the triangle is a right triangle. In drawing right triangles, the interior 90° angle is indicated with a little square □ in the vertex.

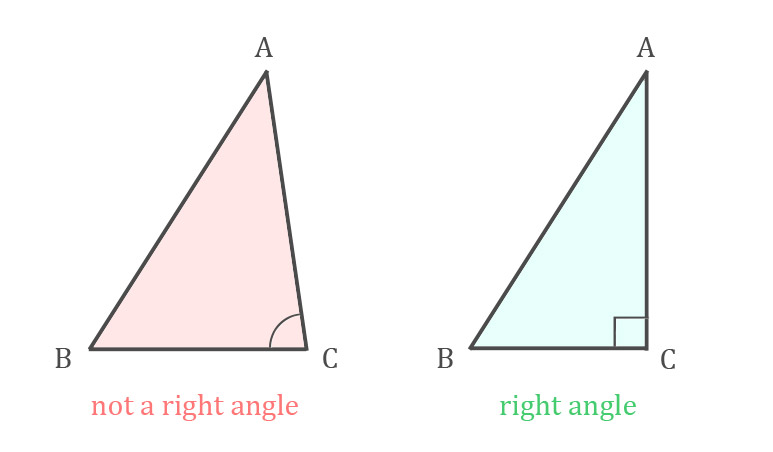
The term "right" triangle may mislead you to think "left" or "wrong" triangles exist; they do not. "Right" refers to the Latin word rectus, meaning "upright."

Hypotenuse and sides of a right triangle

We already know the square vertex of the right triangle is a right angle. Opposite it is the triangle's hypotenuse, the longest of the three sides, usually labeled c.

The other two angles in a right triangle add to 90°; they are complementary. The sides opposite the complementary angles are the triangle's legs and are usually labeled a and b.

Properties of right triangles

Construct a right angled triangle

Use two uncooked spaghetti strands to make your own right triangle. Leave one alone; break the other strand into two unequal lengths.

Place the two short strands a and b so they meet at two endpoints and form a 90° angle. Laying the third strand c down to intersect the two endpoints of aa and bb creates a right triangle.

You can make a more accurate right triangle by using graph paper and a straightedge. Draw a line segment (of any desired length) along the graph paper's printed lines. Follow the lines to make a second line segment exactly 90° to your first line segment, of any desired length.

If you connect the two endpoints of those line segments, you have a right triangle.

Geometry uses symbols as shorthand. Here are important ones to know:

• ∼ means "similar"

• ∠ means "angle"

• △ means "triangle"

The Pythagorean theorem

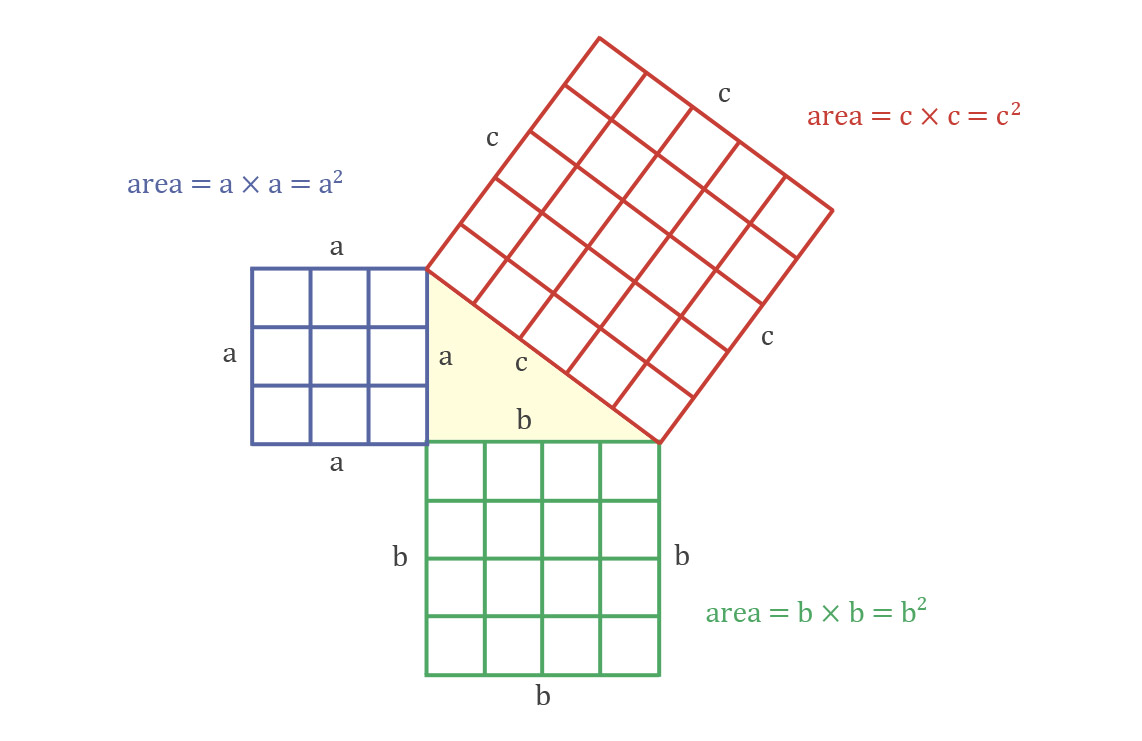
Greek mathematician Pythagoras gets the credit, but other civilizations knew about this theorem. The Pythagorean Theorem describes the relationship between the lengths of legs a and b of any right triangle to the length of hypotenuse, c:

The sum of the squares of legs, a and b, are equal to the square of hypotenuse, c, or

Thousands of proofs of this theorem exist, including one by U.S. president James Garfield (before he became president). One proof is easy to make with graph paper, a straightedge, pencil, and scissors.

Construct △ABC with legs, a and b, to the left and bottom and hypotenuse, c at the top right. Leg a is opposite ∠A, leg bb is opposite ∠B, and hypotenuse cc is opposite right angle C.

Let length a=3, b=4, and hypotenuse c=5.

Construct a square using leg aa as the right side of the square. It will be 9 square units (${a}^{2}$). Construct a square using leg b as the top side of its square, so it is 16 square units (${b}^{2}$). Cut out another 5 x 5 square and line it up with hypotenuse, c, so the square is ${c}^{2}$.

Think: what is 9 square units + 16 square units? It is 25 square units, the area of ${c}^{2}$.

Right triangle altitude theorem

The right triangle altitude theorem tells us that the altitude of a right triangle drawn to the hypotenuse c forms two similar right triangles that are also similar to the original right triangle.

Construct △ABC so that hypotenuse c is horizontal and opposite right angle C, meaning legs aa and bb are intersecting above c to form the right angle C. This puts ∠A to the bottom left, and ∠B to the bottom right.

Construct an altitude (or height) h from the interior right angle C to hypotenuse c (so it is perpendicular to c).

This altitude h creates two smaller triangles inside our original triangle. The altitude divided ∠C, and also created two right angles where it intersected hypotenuse c.

Call the point where the altitude h touches hypotenuse, c, point D. You now have two triangles, △ACD and △BCD. Each of these triangles is similar to the other triangle, and both are similar to the original triangle.

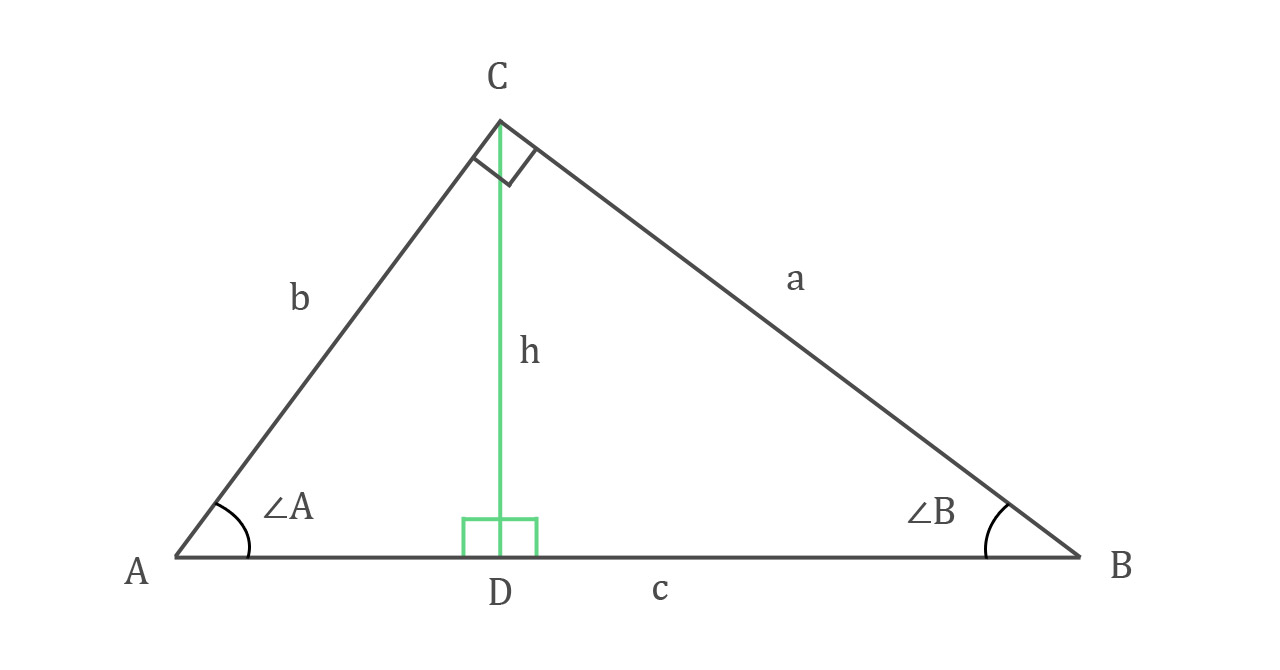
You can prove this by seeing that new triangle's ∠ADC = original triangle's ∠ACB, while new triangle's ∠CAD = original triangle's ∠CAB.

This means two angles of △ADC and △ABC are similar, making the triangles themselves similar (by the Angle-Angle postulate or AA postulate):

Go through the figure again, concentrating on the larger, new triangle BCD. Here ∠BDC = ∠ACB, and ∠DBC = ∠ABC, so again, (by the AA postulate):

Since each of the two smaller triangles are similar to the larger triangle, they are similar to each other. So:

Lesson summary

After going through the videos, reading the lesson and examining the pictures, you now know how to identify a right triangle (by its interior right angle), what its identifying property is (it has one interior right angle).

You also know what the Pythagorean Theorem is (${a}^{2}+{b}^{2}={c}^{2}$) and how to prove it, and what the right triangle altitude theorem is (the altitude of a right triangle drawn to the hypotenuse, c, forms two similar right triangles that are also similar to the original right triangle) and how to prove it.