Hypotenuse — Definition & Formula
Hypotenuse definition
In geometry, very few polygons get their own special terms. The word hypotenuse is reserved exclusively for the longest side of a right triangle. No other triangle can have a side labeled a hypotenuse.
The mathematical term "hypotenuse" comes down through the ages to us from a Greek word whose origin meant "stretching under," and when you look at a right triangle, you can almost feel the tension in that longest side, the hypotenuse. The hypotenuse of a right triangle has some interesting properties and is useful in both geometry and trigonometry.
What is a right triangle?
A right triangle has the required three sides and three interior angles. One of its interior angles is a right angle, opposite the hypotenuse, with the other two sides - legs - meeting to form that right angle. In a right triangle a leg can also be called a cathetus (plural: catheti).
The two legs are, by definition, two altitudes or heights of the right triangle; the third altitude can be constructed by striking a perpendicular line segment from the hypotenuse to the right angle.
Hypotenuse formula
Pythagoras was a Greek mathematician and philosopher who is still remembered for the Pythagorean Theorem, probably developed not by him but by the school of thought he created:
The Pythagorean theorem
Where a and b are the legs of a right triangle and c is the hypotenuse.
Here is a right triangle, , with leg HY measuring 5 meters and YP measuring 12 meters. How long is the hypotenuse?
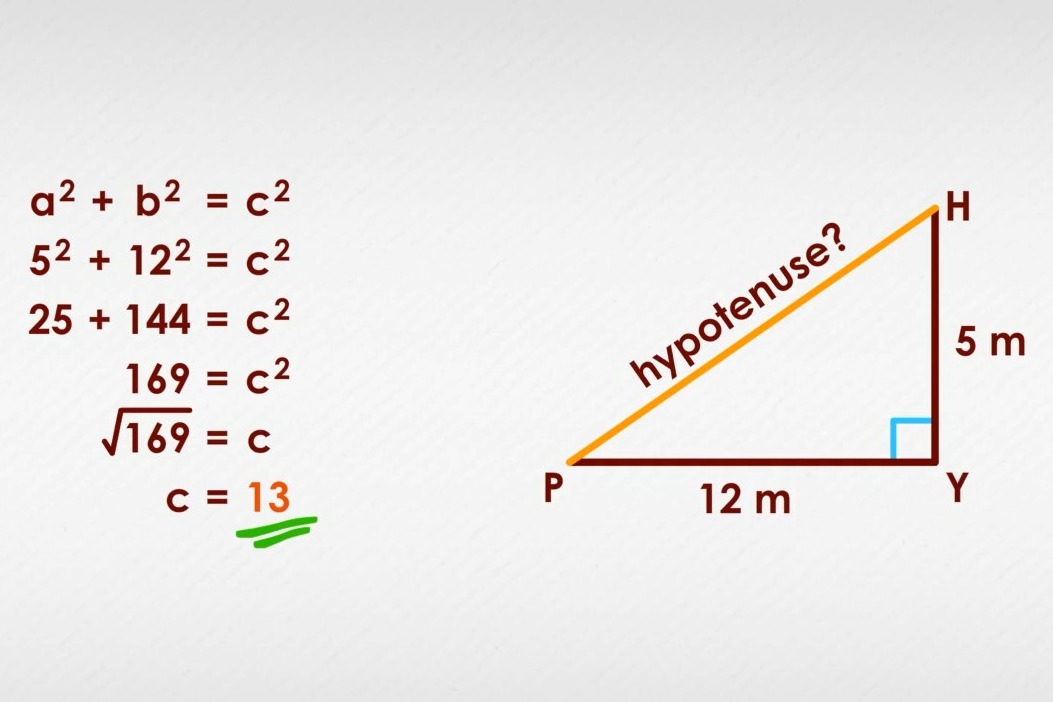
That was neat and simple because we used a Pythagorean Triple for our numbers; the measure of a hypotenuse may extend to several decimal places, requiring a calculator for the square root.
Trigonometry
Just as the word "hypotenuse" is reserved for the longest side of right triangles, trigonometry is a word reserved for the special branch of mathematics dealing exclusively with the relationships between sides and angles of triangles. The word itself comes from Greek words meaning "triangle measure."
The mathematical relationships between sides and angles are called trigonometric functions:
sine - sin x
cosine - cos x
tangent - tan x
And their reciprocals:
cosecant - csc x
secant - sec x
cotangent - cot x
The Greek letter theta, , is used for the angle adjacent to the hypotenuse of the right triangle, and the leg opposite is referred to as the opposite. The trigonometric functions that allow you to solve for lengths of sides are:
sine = opposite over hypotenuse
cosine = adjacent over hypotenuse
tangent = opposite over adjacent
cosecant = hypotenuse over opposite
secant = hypotenuse over adjacent
tangent = adjacent over opposite
SOHCAHTOA
A mnemonic is a memory device that can help you sort out important information. SOHCAHTOA is a mnemonic for the three relationships:
SOH - sine = opposite over hypotenuse
CAH - cosine = adjacent over hypotenuse
TOA - tangent = opposite over adjacent
How to find the hypotenuse
Here is a very long, short, right triangle, , with and . We know the distance of horizontal leg (cathetus) OW is 25 feet, but we do not know the height of the triangle (vertical leg or cathetus LO).
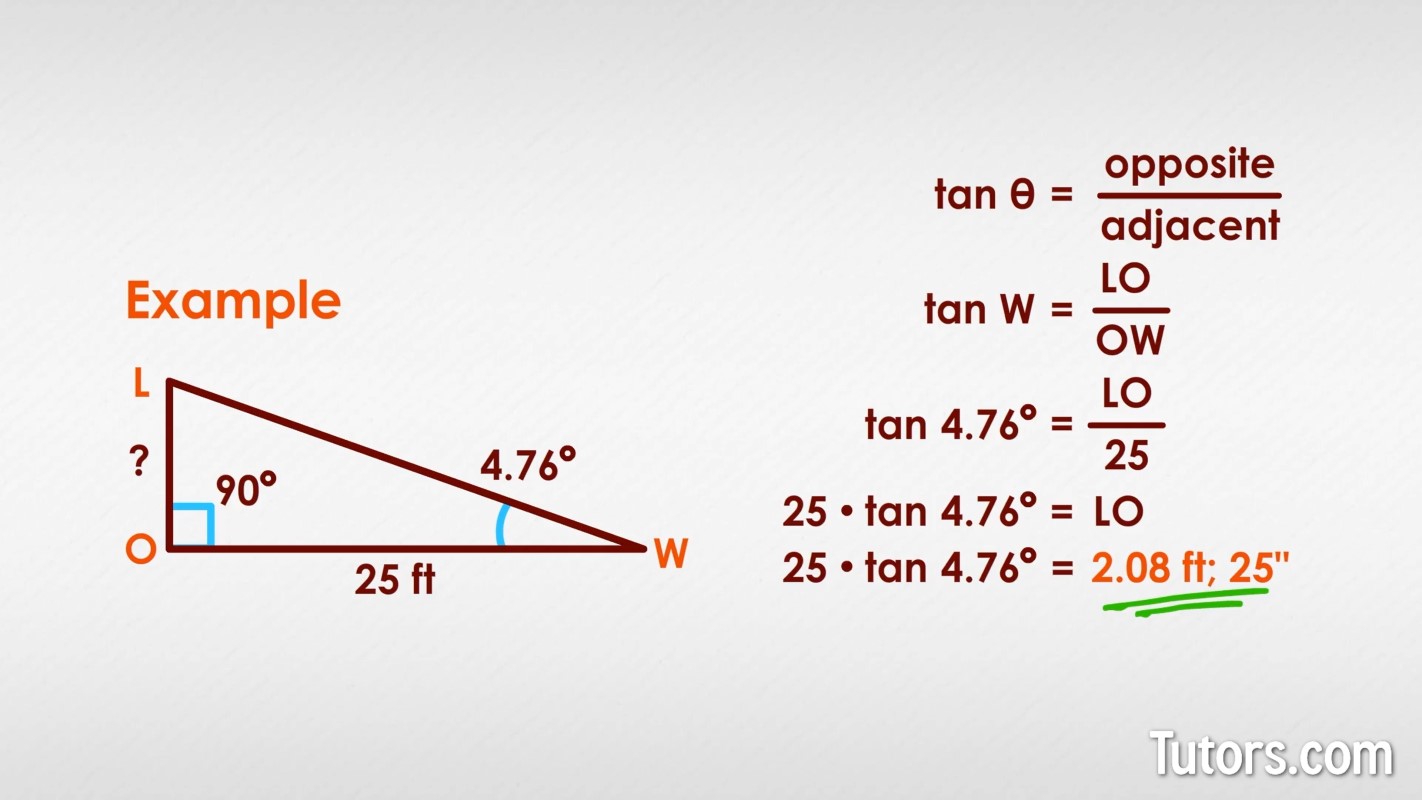
We know an angle and one side. The side is adjacent to our known angle. We want to know the length of the opposite side. So we use opposite over adjacent, or tangent:
Multiply both sides by 25 to isolate our unknown:
You'll need a calculator to solve :
The height of cathetus (leg) LO, 25", is not a random number. That is the proper height for a 25' handicap ramp using the recommended angle for such ramps, 4.76°. Trigonometry has real-world applications all around you!
Lesson summary
Now that you have gone carefully through the lesson, you are able to recall the definition of a hypotenuse, recognize and identify the hypotenuse of any right triangle, and use trigonometry to find the length of an unknown side, or the measure of an unknown angle.