How to Find the Height of a Triangle
How to find the height of a triangle
A triangle's height is the length of a perpendicular line segment originating on a side and intersecting the opposite angle. Every triangle has three heights, or altitudes, because every triangle has three sides.
In an equilateral triangle, like △SUN below, each height is the line segment that splits a side in half and is also an angle bisector of the opposite angle. That will only happen in an equilateral triangle.
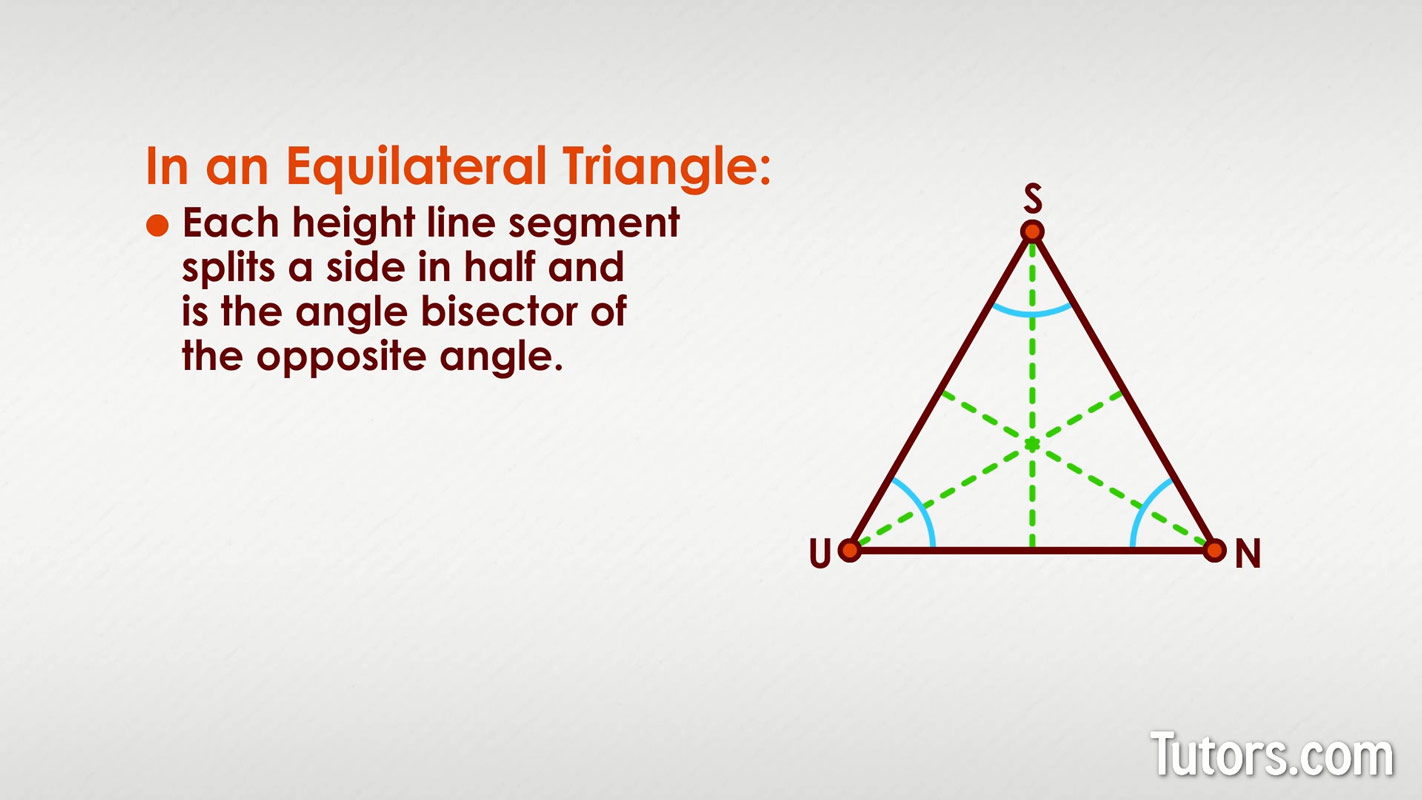
By definition of an equilateral triangle, you already know all three sides are congruent and all three angles are 60°.
If △SUN has one side labelled 24 cm, then all three sides are 24 cm. Each line segment showing the height from each side also divides the equilateral triangle into two right triangles.
You can see that the line segment showing a height bisects the side, so the short leg of the newly created right triangle is 12 cm. We already know the hypotenuse is 24 cm.
Height of a triangle formula
You can take any side of our splendid △SUN above and see that the line segment showing its height bisects the side, so each short leg of the newly created right triangle is 12 cm, and we already know the hypotenuse of our new right triangle is 24 cm.
Knowing all three angles and two sides of a right triangle, what is the length of the third side? This is a job for the Pythagorean theorem.
Using Pythagorean theorem
Focus on the lengths; angles are unimportant in the Pythagorean theorem. Plug in what you know:
Most people would be happy to say the height (side b) is approximately 20.78, or b ≈ 20.78.
You can decide for yourself how many significant digits your answer needs, since the decimal will go on and on. Do not forget to use linear measurements for your answer!
The Pythagorean Theorem solution works on right triangles, isosceles triangles, and equilateral triangles. It will not work on scalene triangles!
Using the area formula to find height
The formula for the area of a triangle is , or . If you know the area and the length of a base, then, you can calculate the height.
In contrast to the Pythagorean Theorem method, if you have two of the three parts, you can find the height for any triangle!
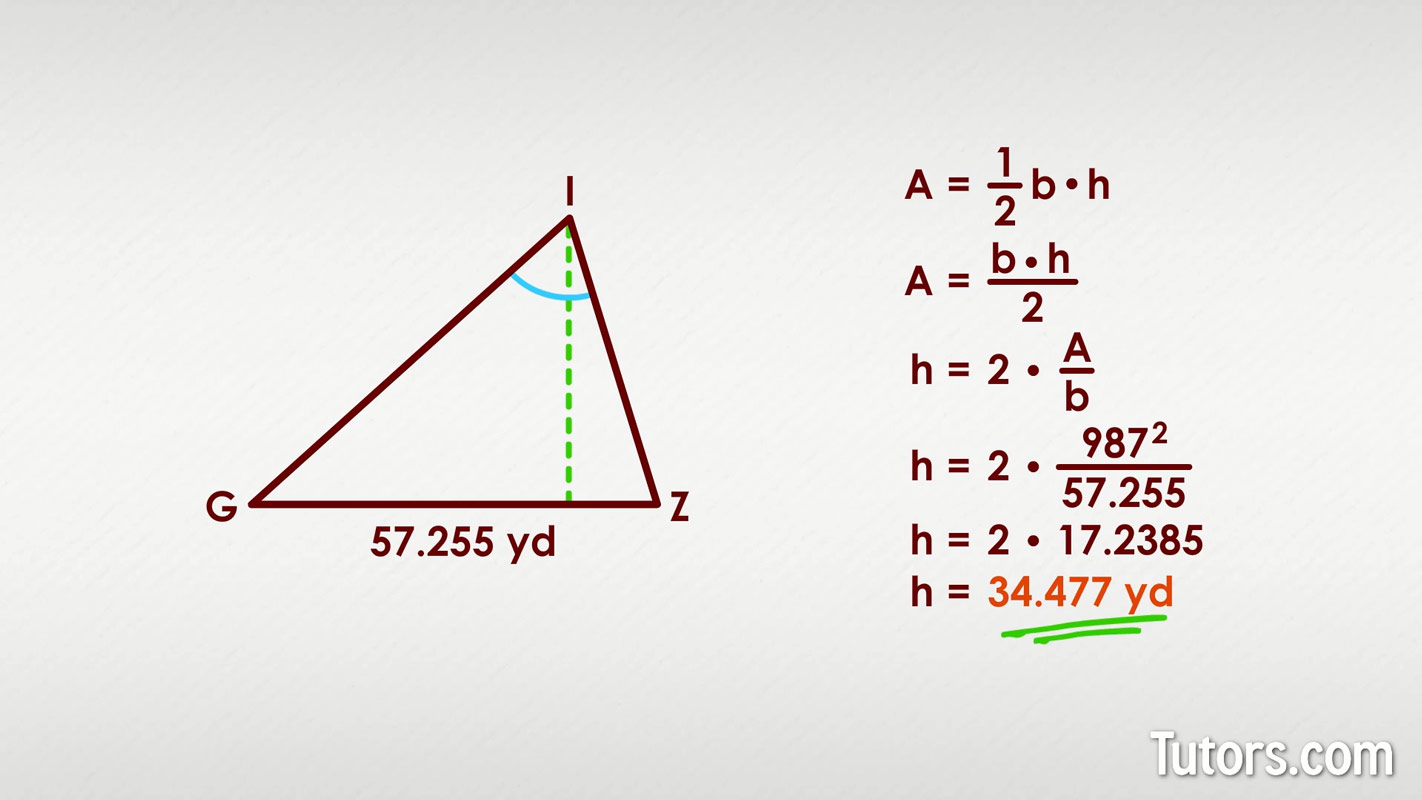
Here we have scalene △ZIG with a base shown as 56 yards and an area of 987 square yards, but no clues about angles and the other two sides:
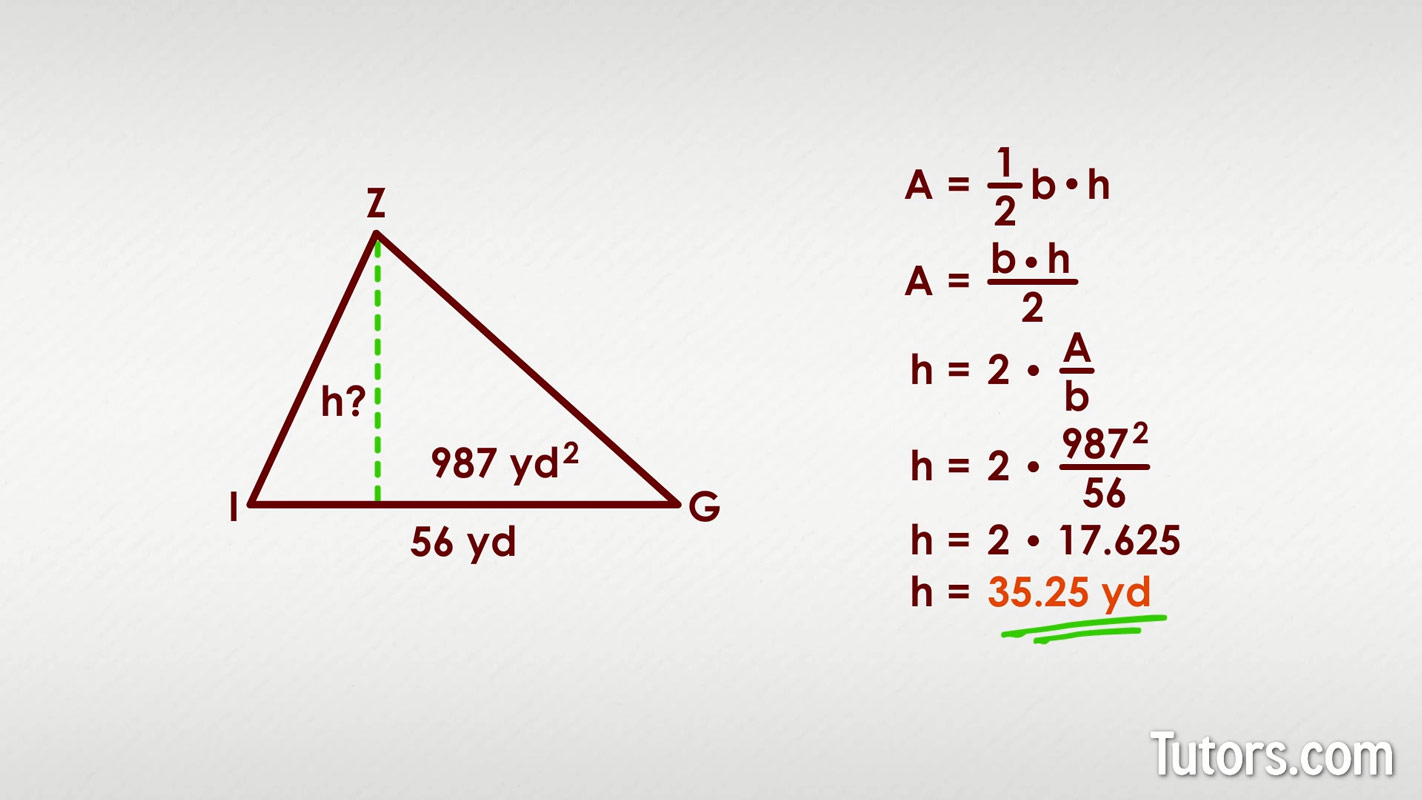
Recalling the formula for area, where A means area, b is the base and h is the height, we remember:
Put in our known values:
Remember how we said every triangle has three heights? If we take △ZIG and rotate it clockwise so side GZ is horizontal, and construct a height up to ∠I, we can get the height for that side, too.