How To Find The Perimeter Of A Triangle — Formula & Examples

Written by

Malcolm McKinsey

January 12, 2023

Fact-checked by

Paul Mazzola

What is a perimeter?

Perimeter is the distance around the sides of a polygon or other shape. Perimeter is always the same linear measurement unit as the unit used for the sides.

Perhaps one of the easiest ways to work with polygons is to find their perimeter, or the distance around their sides. The triangle is the simplest polygon, so finding its perimeter is simple!

In the equilateral triangle below, $\triangle WUT$ has sides WU, UT, and TW. The little tick marks on the sides indicate that all three sides are the same, so the measurement for WU, 27 meters, is also true for the other two sides.

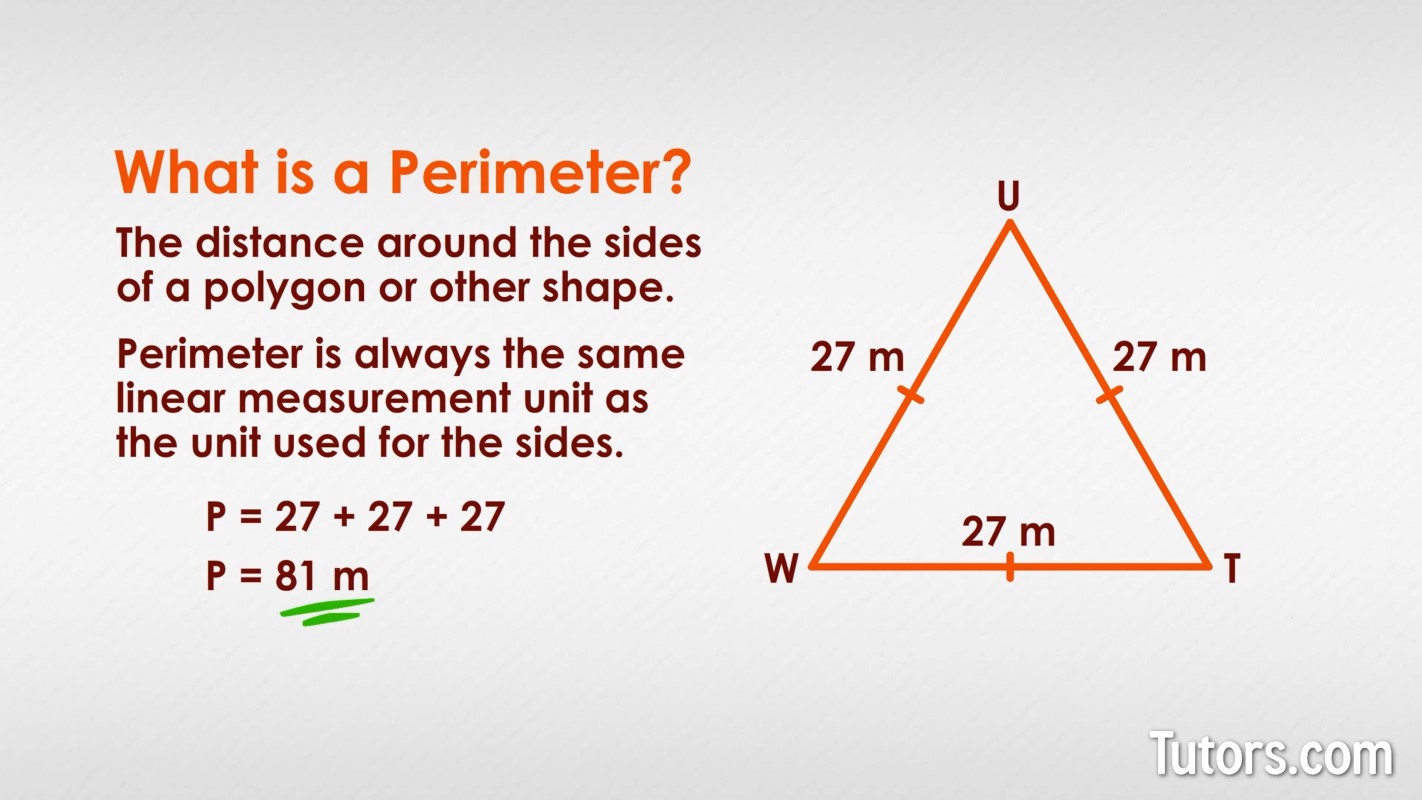
To find the perimeter of the triangle, add up the lengths of the three sides:

Triangle classifications

A triangle is a three-sided, flat shape that closes in a space. The three sides form three interior angles. Triangles come in many configurations, depending on your choice to focus on their sides or their angles:

By sides

• Equilateral - Three equal-length sides

• Isosceles - Two equal-length sides, called legs

• Scalene - No equal-length sides

By angles

• Acute - Three interior angles < 90°

• Obtuse - One interior angle > 90°

• Right - One interior angle = 90°

Acute and obtuse triangles are in a category called oblique triangles, which means they have no right angles. Right triangles have one right angle.

Formula for perimeter of a triangle

You can find the perimeter of every one of these triangles using this formula:

This is always true where P is perimeter and a, b, and c are the lengths of the sides.

Perimeter of equilateral triangles

Only with equilateral triangles can you substitute multiplication for addition. Since equilateral triangles have three equal sides, $P=3\times a$, or $P=3a$ where P is perimeter and a is the length of any side.

How to find the perimeter of a triangle

Here is scalene triangle DOT with measured sides of 9 yards, 11 yards, and 13 yards:

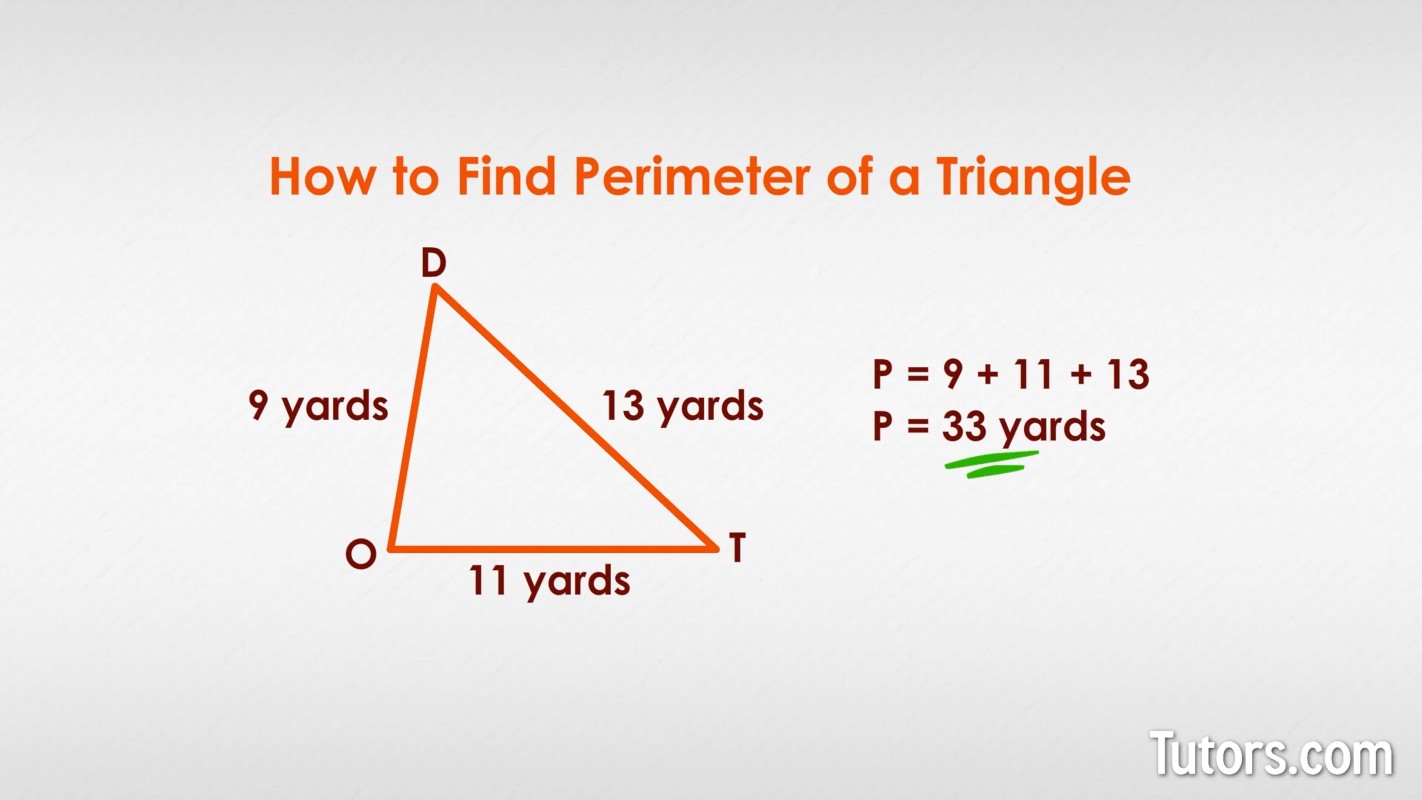
Add up the three lengths:

Here is isosceles triangle LEG, with base EG measuring 175 mm. Only one leg is measured, $LE=200 mm$.

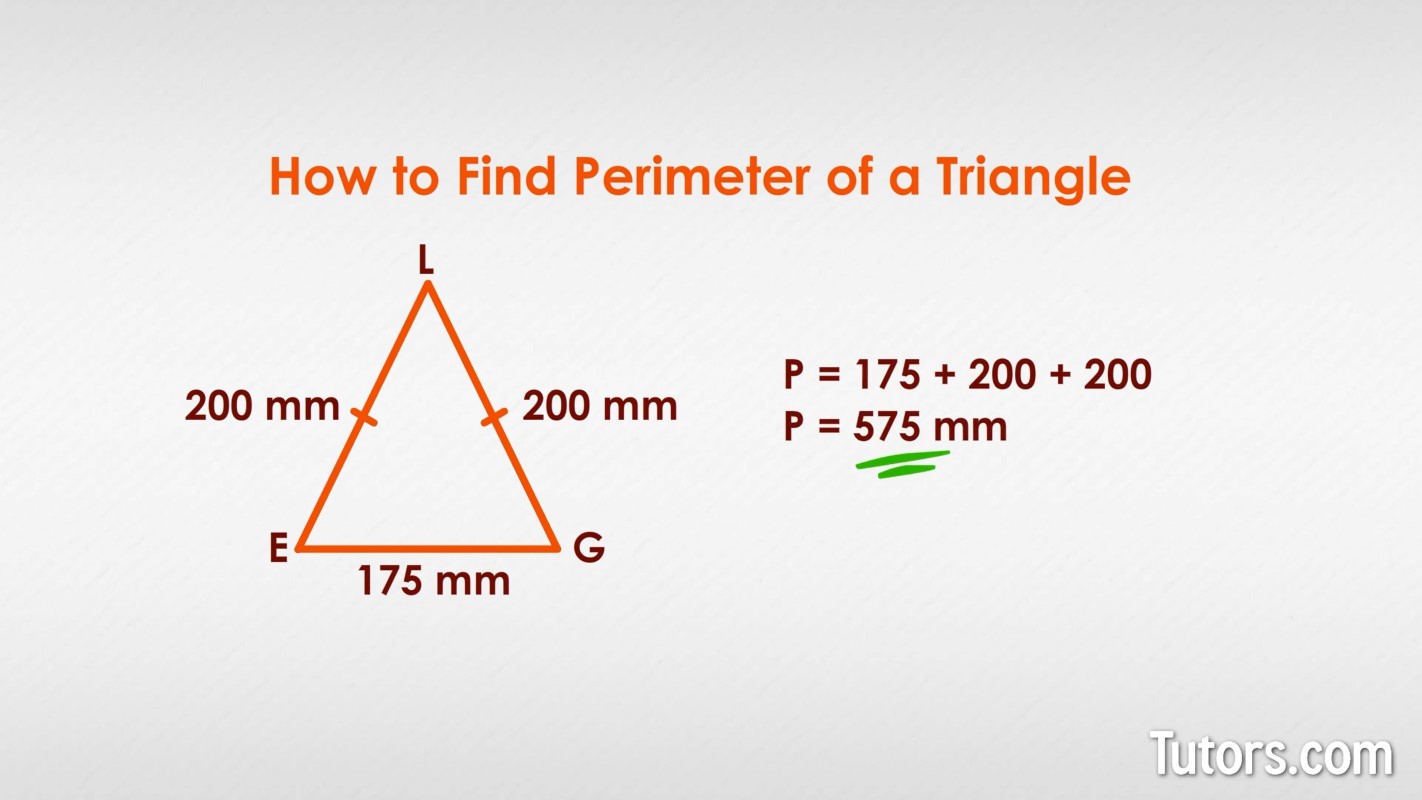
How long is side GL? 

In an isosceles triangle, the other leg is equal to the identified leg, so you also know $GL=200 mm$! Add up the sides:

Algebra perimeter challenge

Some textbooks and mathematics teachers can take a simple concept like perimeter of triangles and turn it into a challenge. Here is $\triangle YAK$ with a given perimeter of 118 km (yes, it's a big triangle) but the sides are identified in an unusual way.

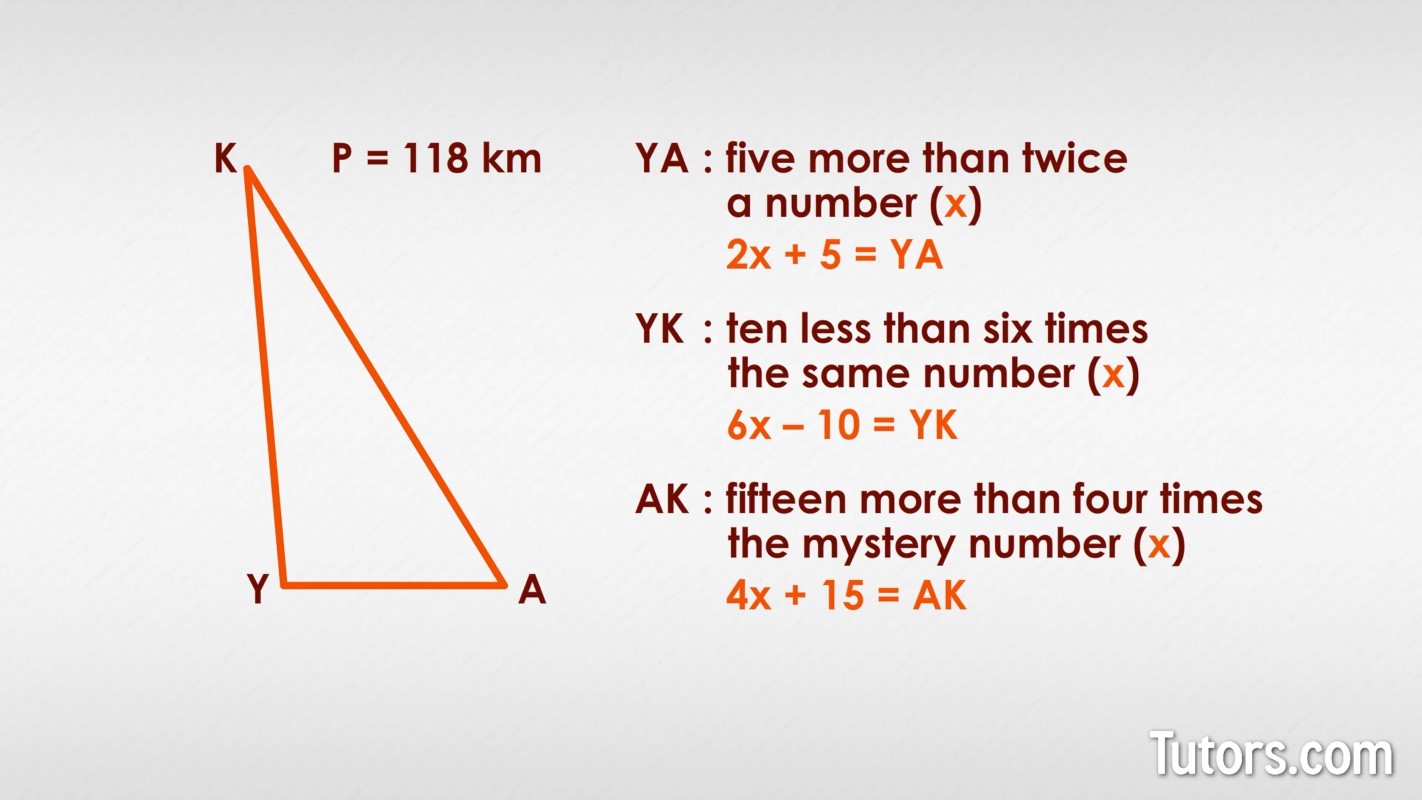
We have side YA as "5 more than twice a number," and YK as "10 less than six times the same number," and side AK as "15 more than four times the mystery number." What are we supposed to do with all that?

Turn each sentence into an algebraic expression. Let x be the unknown number:

"5 more than twice a number" becomes:

"10 less than six times the same number" becomes:

"15 more than four times the mystery number" becomes:

Perimeter is the sum of the sides, so if you put these expressions together, you get:

Combine terms:

Subtract 10 from both sides to isolate the variable:

Divide both sides by 12:

Go back to each expression and replace x with 9 km:

...

...

To confirm our sides, add to see if they equal the given perimeter:

Well done! You used algebra to solve a perimeter problem!

Lesson summary

Now that you have worked your way through the lesson, you are able to define perimeter, recognize the types of triangles, recall and explain a method of finding the perimeter of triangles by adding the lengths of their sides, and, given perimeter, solve for lengths of sides of a triangle using algebra.