How to find the area of a right triangle

Written by

Malcolm McKinsey

January 15, 2023

Fact-checked by

Paul Mazzola

Area of a right triangle

The right triangle comes along frequently in geometry. It is used over and over for examples, since it offers a readymade right angle, a hypotenuse, and other great parts. Finding the area of a right triangle is easy and fast.

Get free estimates from geometry tutors near you.

Right triangle

Let's create a right triangle, $\triangle CAS$ , with $\angle A$ as the right angle. It measures 90° and has the hypotenuse, or longest side, opposite it. That is side SC, 30 yards long. It is a right triangle because it has a right angle, not because it is facing to the right.

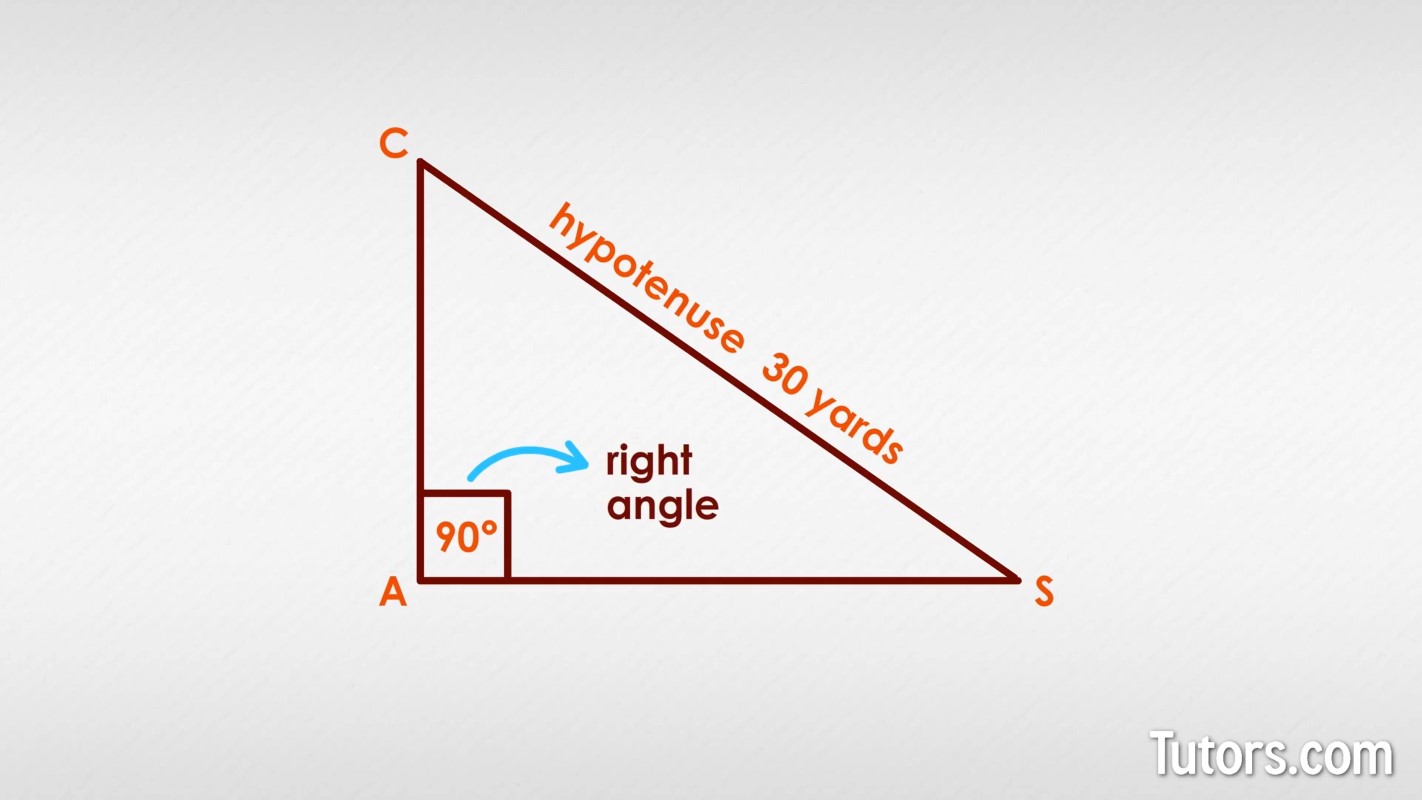
The word "right" refers to the Latin word rectus, which means upright. A right angle shows one line or line segment upright from another; a right triangle has an upright angle.

Base

The base of any triangle is the side used to create an altitude, or height, to an opposite vertex. The way our $\triangle CAS$ is sitting, you can easily see that side AS is the base for the altitude CA to $\angle C$ . Side CA is the base for the altitude AS.

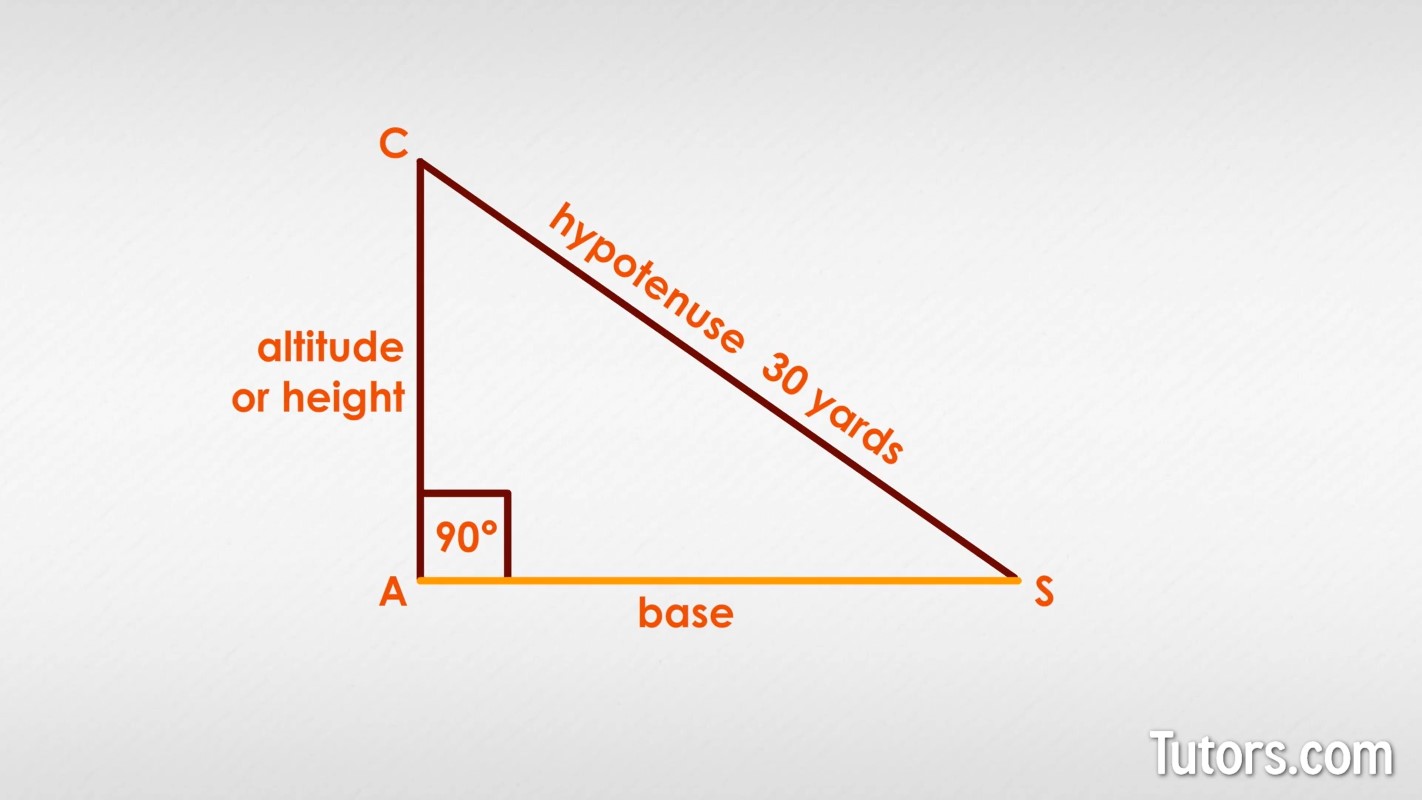
For a right triangle, the sides adjacent to the right angle serve double duty as bases and altitudes, making the calculations of area really, really easy.

Altitude or height

Get free estimates from geometry tutors near you.

The altitude of any triangle is the perpendicular from a base (side) to the opposite vertex. For our $\triangle CAS$ we can rotate the figure one more time and place side SC on the horizontal, then construct an altitude from $\angle A$ down to the base. The point where it intersects SC can be labelled H. Now we have $\triangle CAS$ and Point H; CASH!

Area of a right triangle formula

The area of a right triangle is the measure of its interior space, in square units. For any triangle, the formula is:

A=\frac{1}{2}(base \times height)

For a right triangle, this is really, really easy to calculate using the two sides that are not the hypotenuse. In our $\triangle CAS$ we can use side AS, 24 yards, as the base, making side CA, 18 yards, the altitude:

A=\frac{1}{2}bh

A=\frac{1}{2}(24\times 18)

A=\frac{1}{2}(432)

A=216 yd{s}^{2}

If we rotate the right triangle and use side CA as the base, AS becomes the altitude, and you get the same answer!

A=\frac{1}{2}(18\times 24)

A=\frac{1}{2}(432)

A=216 yd{s}^{2}

Rotate it one more time and use side SC, 30 yards, as the base, with constructed altitude AH, which is 14.4 yards in height:

A=\frac{1}{2}bh

A=\frac{1}{2}(30\times 14.4)

A=\frac{1}{2}(432)

A=216 yd{s}^{2}

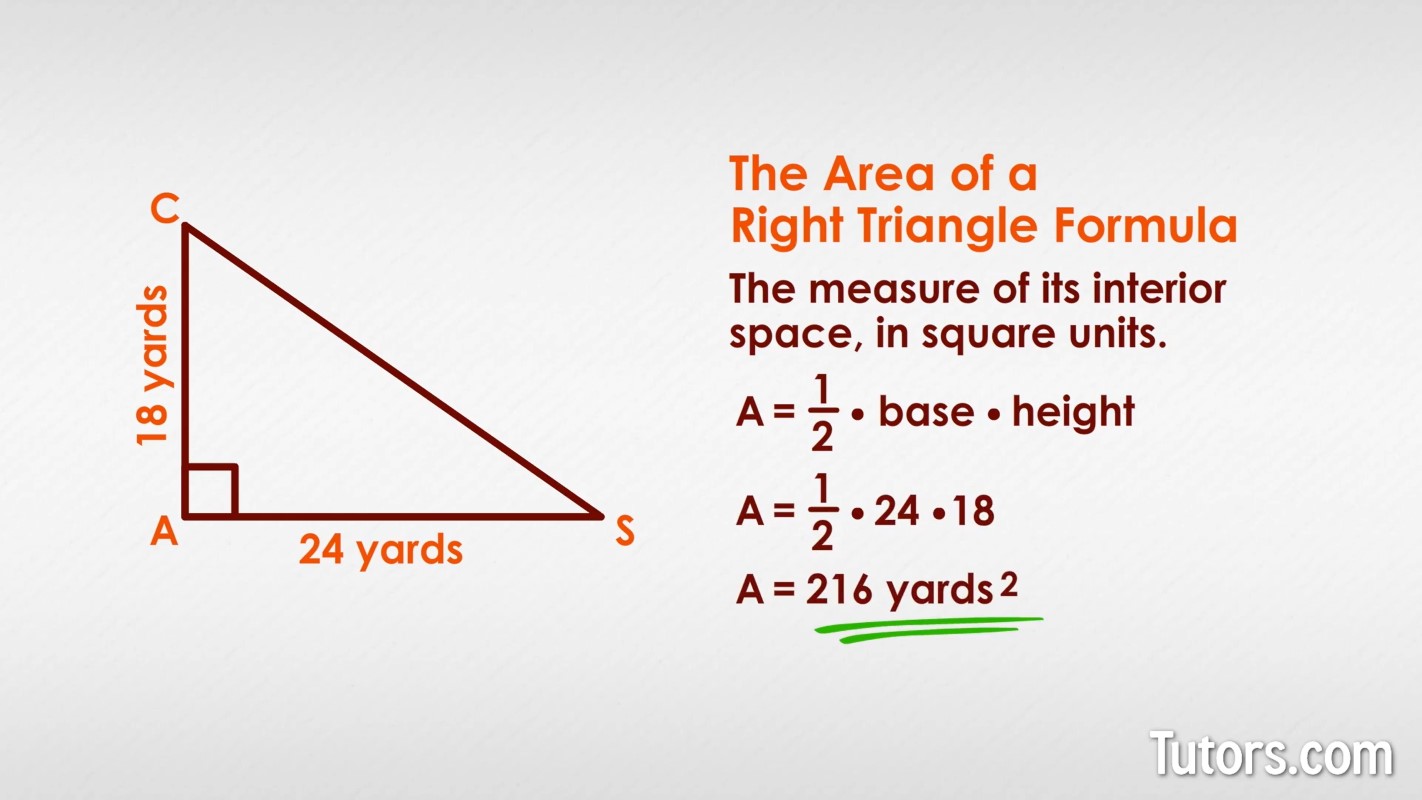
All three sides, all three altitudes or heights, and all three answers the same! Remember the area is always in square units of the linear measurement (yards, in our triangle).

Lesson summary

After reviewing this lesson, you are now able to identify a right triangle, manipulate a right triangle to find all its altitudes or heights, and recall and apply the formula $\frac{1}{2}$ (base x height) to find the area of a right triangle.