How to Find the Orthocenter of a Triangle
What is the orthocenter of a triangle?
The orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot).
You can find where two altitudes of a triangle intersect using these four steps:
Find the equations of two line segments forming sides of the triangle
Find the slopes of the altitudes for those two sides
Use the slopes and the opposite vertices to find the equations of the two altitudes
Solve the corresponding x and y values, giving you the coordinates of the orthocenter
Those may sound like four easy steps, but embedded within them is the knowledge to find two equations:
The equation of a line
The equation of a perpendicular line
Triangles and their parts
A triangle, the simplest polygon with only three straight line segments forming its sides, has several interesting parts:
Sides – Three sides intersecting at vertices, forming three interior angles
Altitudes – The line segment from each vertex of the triangle to the opposite side (or extension of the opposite side) that is perpendicular to that opposite side. Because the segment from the interior angle to the opposite side is perpendicular, an altitude of a triangle will always form a right angle with the side to which it is perpendicular.
Orthocenter – The intersection of the three altitudes.
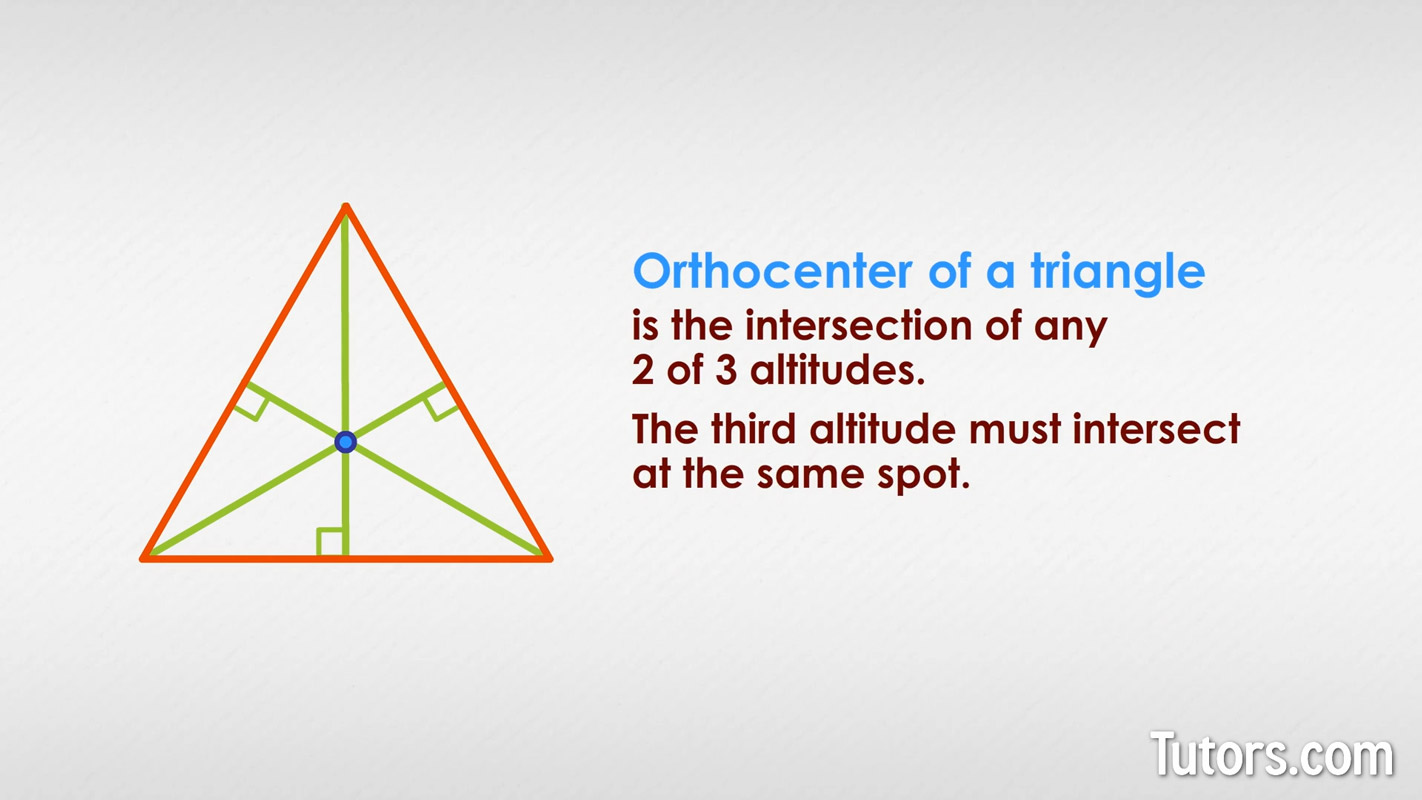
It doesn't matter if you are dealing with an acute triangle, obtuse triangle, or a right triangle, all of these have sides, altitudes, and an orthocenter.
In addition to the orthocenter, there are three other types of triangle centers:
Incenter – The incenter of a triangle is located where all three angle bisectors intersect.
Circumcenter – The circumcenter is located at the intersection of the perpendicular bisectors of all sides. This will occur inside acute triangles, outside obtuse triangles, and for right triangles, it will occur at the midpoint of the hypotenuse.
Centroid – The centroid, or a triangle's center of gravity point, is located where all three medians intersect.
Orthocenter – The orthocenter lies at the intersection of the altitudes.
All four of the centers above occur at the same point for an equilateral triangle.
Another interesting fact is that the orthocenter, centroid, and circumcenter of any triangle are collinear. These three points will always lie on the same straight line, which is called the Euler line. The Euler line is named after it's discoverer, Leonhard Euler.
How to find the orthocenter of a triangle
Here we have a coordinate grid with a triangle snapped to grid points:
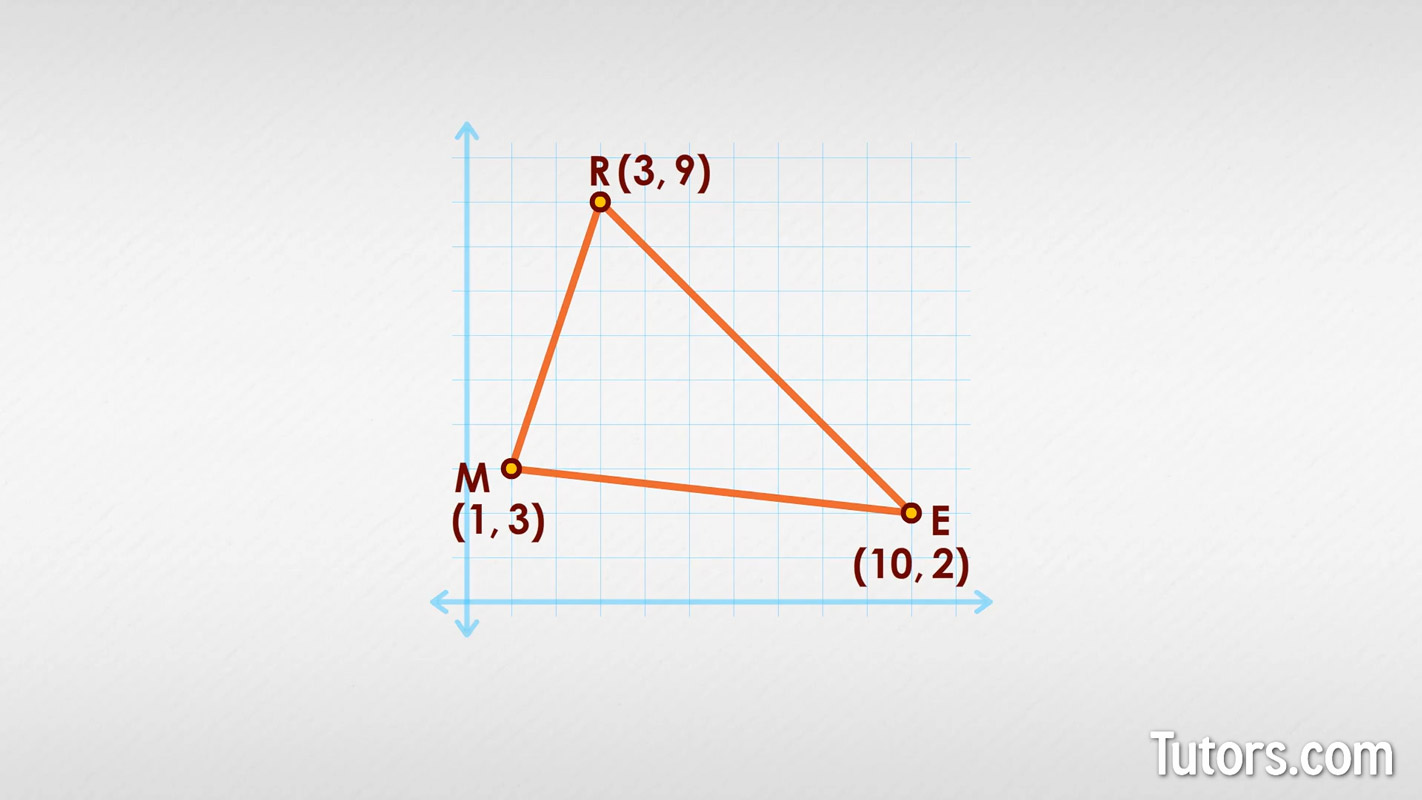
Point M is at (1, 3)
Point R is at (3, 9)
Point E is at (10, 2)
Step one
Find the equations of lines forming sides MR and RE. You do this with the formula y = mx + b, where m is the slope of the line, and b is the y-intercept.
To find the slope of line MR, you plug in the coordinates as the change in y values over the change in x values:
For our triangle's side MR, it looks like this:
Return to your equation and plug in 3 for m:
You already have x and y values, so use either given point and plug in its numbers. Use Point M, for example:
You can test this by using Point R (it will give the same answer):
So for line segment MR the equation of the line is
Repeat these for line segment RE and you find the question of the side RE is That was all just step one!
Step two
For step two, find the slopes of perpendiculars to those given sides. You need the slope of each line segment:
For side MR,
For side ME,
To find the slope of a line perpendicular to a given line, you need its negative reciprocal:
For side MR,
For side RE,
Step three
For step three, use these new slopes and the coordinates of the opposite vertices to find the equations of lines that form two altitudes:
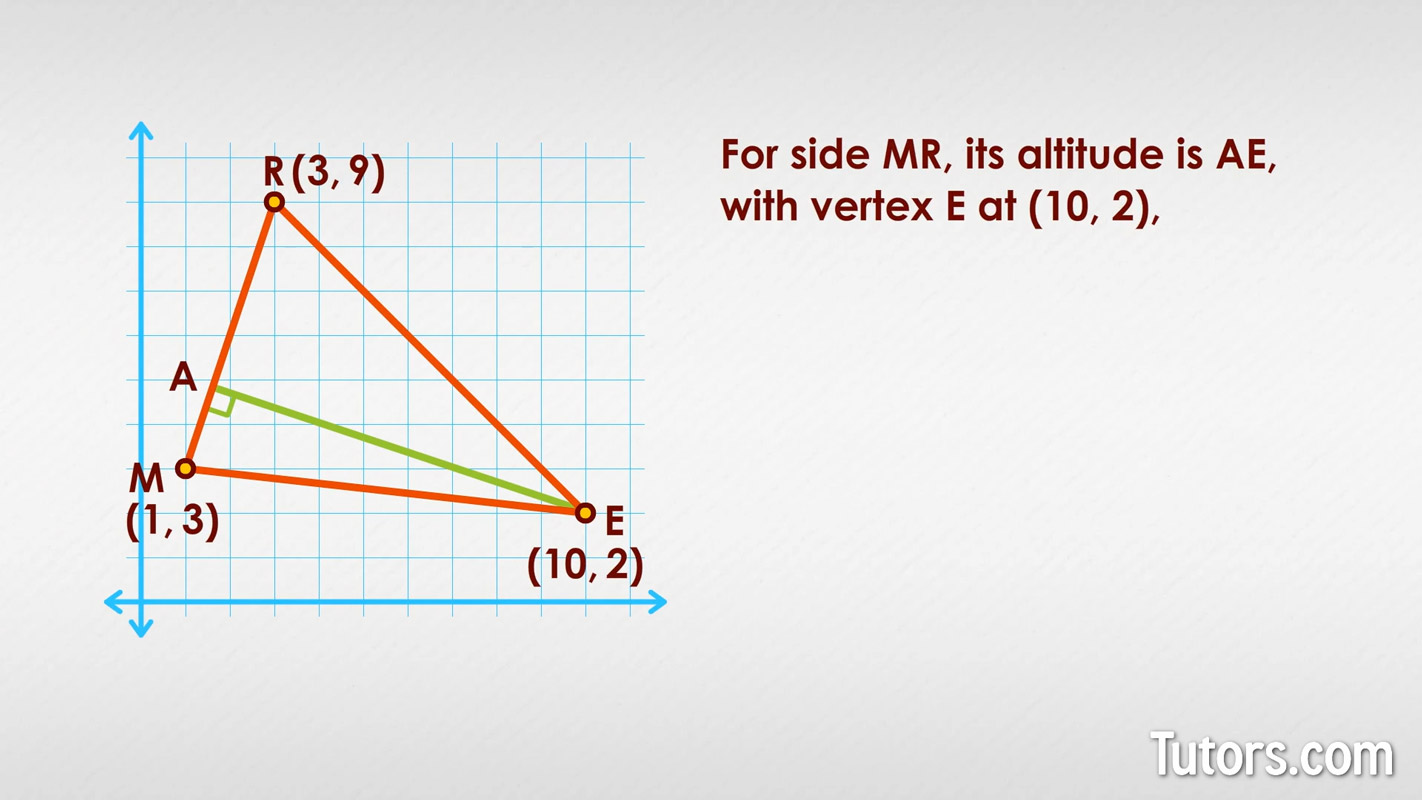
For side MR, its altitude is AE, with vertex E at (10, 2), and :
The equation for altitude AE is .
For side RE, its altitude is VM, with vertex M at (1, 3), and :
The equation for altitude VM is .
Step four
You can solve for two perpendicular lines, which means their x and y coordinates will intersect:
Solve for each coordinate; first for x:
Solve for y, using either equation and plugging in the found x:

Test it with the other equation:
The orthocenter of the triangle is at (2.5, 4.5). Whew! Four (long) but valuable steps.
Orthic triangle and the circumcircle
Working through these examples, you may have noticed a smaller triangle is formed by the feet of the three altitudes. This smaller triangle is called the orthic triangle. There are many interesting properties of the orthic triangle for you to discover, such as the circumcircle of the orthic triangle, also called the nine-point-circle of a triangle.