30-60-90 Triangle (Theorem, Ratio, & Formula)
What is a 30-60-90 triangle?
A 30-60-90 triangle is a right triangle where the three interior angles measure 30°, 60°, and 90°. Right triangles with 30-60-90 interior angles are known as special right triangles.
Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides.

In all triangles, the relationships between angles and their opposite sides are easy to understand. The greater the angle, the longer the opposite side.

This means, of the three interior angles, the largest interior angle is opposite the longest of the three sides, and the smallest angle will be opposite the shortest side.
In a right triangle, recall that the side opposite the right angle (the largest angle) is called the hypotenuse (the longest side, and the other two sides are called legs.
30-60-90 triangle ratio
A 30-60-90 degree triangle is a special right triangle, so it's side lengths are always consistent with each other. The ratio of the sides follow the 30-60-90 triangle ratio:
Short side (opposite the 30 degree angle) = x
Hypotenuse (opposite the 90 degree angle) = 2x
Long side (opposite the 60 degree angle) = x√3

30-60-90 triangle theorem
These three special properties can be considered the 30-60-90 triangle theorem and are unique to these special right triangles:
The hypotenuse (the triangle's longest side) is always twice the length of the short leg
The length of the longer leg is the short leg's length times √3
If you know the length of any one side of a 30-60-90 triangle, you can find the missing side lengths
Other interesting properties of 30-60-90 triangles are:
All 30-60-90 triangles are similar
Two 30-60-90 triangles sharing a long leg form an equilateral triangle

How to solve a 30-60-90 triangle
Education is knowing that 30-60-90 triangles have three properties laid out in the theorem. Wisdom is knowing what to do with that knowledge. Suppose you have a 30-60-90 triangle:

We know that the hypotenuse of this triangle is twice the length of the short leg:
We also know that the long leg is the short leg multiplied times the square root of 3:
We set up our special 30-60-90 to showcase the simplicity of finding the length of the three sides. Try figuring this one out:

The long leg is the short leg times √3, so can you calculate the short leg's length? Did you say 5?
The length of the hypotenuse is always twice the short leg's length. Did you get 10?
You can create your own 30-60-90 Triangle formula using the known information in your problem and the following rules. This table of 30-60-90 triangle rules to help you find missing side lengths.
30-60-90 triangle rules
| If you know... | Then... | To get... |
|---|---|---|
| Hypotenuse | Divide by 2 | Short leg |
| Short leg | Multiply by 2 | Hypotenuse |
| Short leg | Multiply by √3 | Long leg |
| Long leg | Divide by √3 | Short leg |
When working with 30-60-90 triangles, you may be tempted to force a relationship between the hypotenuse and the long leg. That relationship is challenging because of the square root of 3.
Work carefully, concentrating on the relationship between the hypotenuse and short leg, then short leg and long leg.
You will notice our examples so far only provided information that would "plugin" easily using our three properties. Sometimes the geometry is not so easy.

What if the long leg is labeled with a simple, whole number?
You leap into the problem since getting the short leg is simply a matter of dividing the long leg by the square root of 3, then doubling that to get the hypotenuse.
But you cannot leave the problem like this:
The rules of mathematics do not permit a radical in the denominator, so you must rationalize the fraction. Multiply both numerator and denominator times √3:
This simplifies to:
Unless your directions are to provide a decimal answer, this can be your final answer for the length of the short side. Doubling this gives 18 √3 for the hypotenuse.
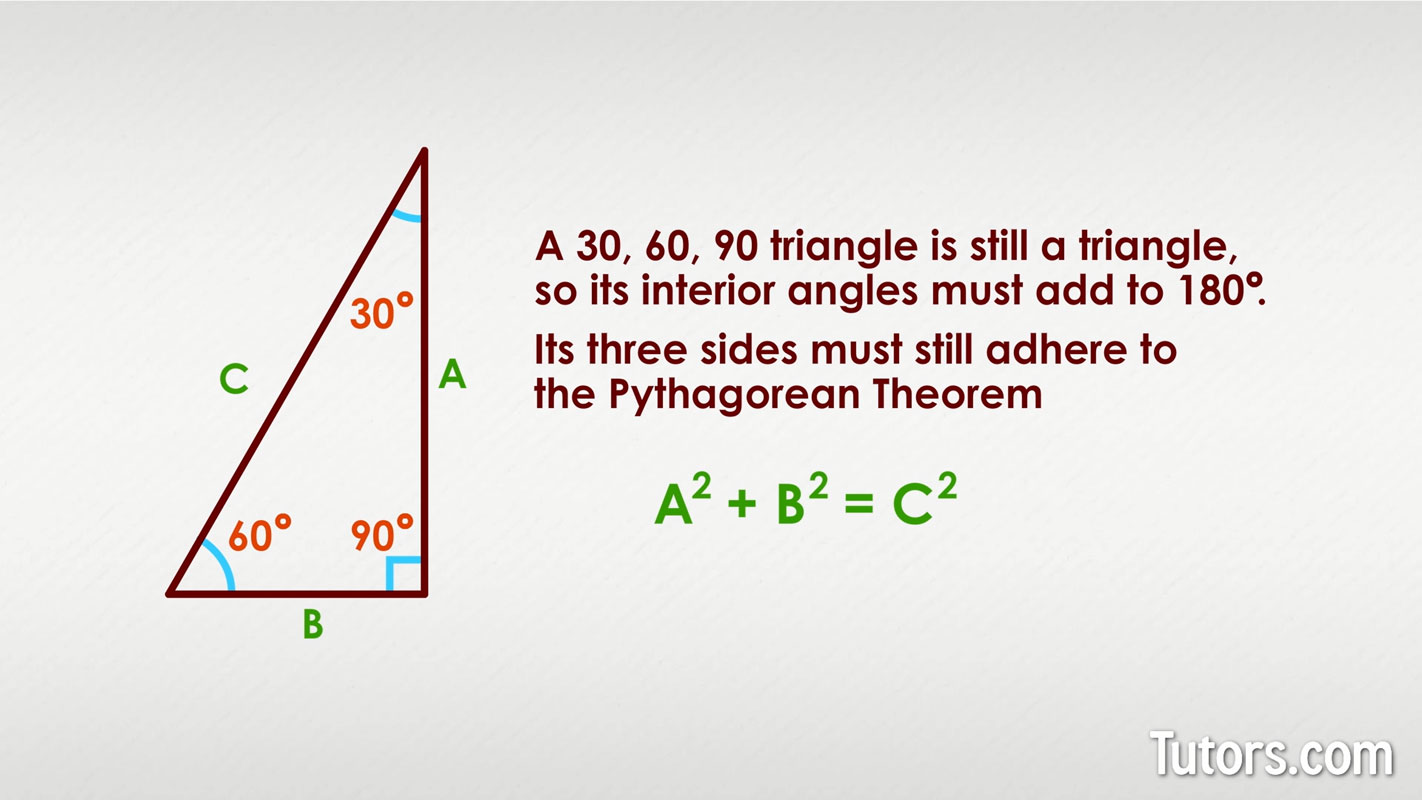
Another warning flag with 30-60-90 triangles is that you can become so engrossed in the three properties that you lose sight of the triangle itself. It is still a triangle, so its interior angles must add to 180°, and its three sides must still adhere to the Pythagorean Theorem:
You can use the Pythagorean Theorem to check your work or to jump-start a solution.
30-60-90 triangle examples
A right triangle has a short side with a length of 14 meters with the opposite angle measuring 30°. What are the other two lengths?

We know immediately that the triangle is a 30-60-90, since the two identified angles sum to 120°:
The missing angle measures 60°. It follows that the hypotenuse is 28 m, and the long leg is 14 m * √3.
What is you have a triangle with the hypotenuse labeled 2,020 mm, the short leg labeled 1,010 mm, and the long leg labeled 1,010√3.
Your knowledge of the 30-60-90 triangle will help you recognize this immediately. You can confidently label the three interior angles because you see the relationships between the hypotenuse and short leg and the short leg and long leg.
Here is a more elaborate problem. What is the length of the shorter leg, line segment MH?:

Did you say 50 inches? This is really two 30-60-90 triangles, which means hypotenuse MA is also 100 inches, which means the shortest leg MH is 50 inches.