Regular Polygons - Definition, Examples & Properties
What is a polygon?
Polygons are straight-sided, flat shapes that close in a space. This means every polygon:
Is two-dimensional
Uses only line segments to create its sides
Has an interior and exterior
The word "polygon" comes from the Greek and means "many angles," because all simple polygons have as many sides as they have angles. The simplest polygon, the triangle, has three interior angles (and three exterior angles!) so it also has three sides.
You can have polygons with so many sides, they appear to be circles even when they are not. Once you get above 10 sides, most mathematics students just say "n-gon," where n is the number of sides or interior angles, as in a "18-gon," or a "25-gon," rather than trying to remember the Greek-origin name.
We have spoken before about polygons, but we have not tackled regular polygons by themselves. They are the crème de la crème of polygons, a class unto themselves!
What is a regular polygon?
To be a regular polygon, the flat, closed, straight-sided shape must also have another property. Every interior and exterior angle in the regular polygon is equal to every other interior and exterior angle, and every side is equal in length to every other side.

A regular polygon has:
Two dimensions
Straight sides
Congruent (equal-length) sides
An interior and exterior
Equal interior angles
Equal exterior angles
Regular polygon examples
A few examples of regular polygons are a triangle, quadrilateral, pentagon, hexagon, heptagon, and a decagon.
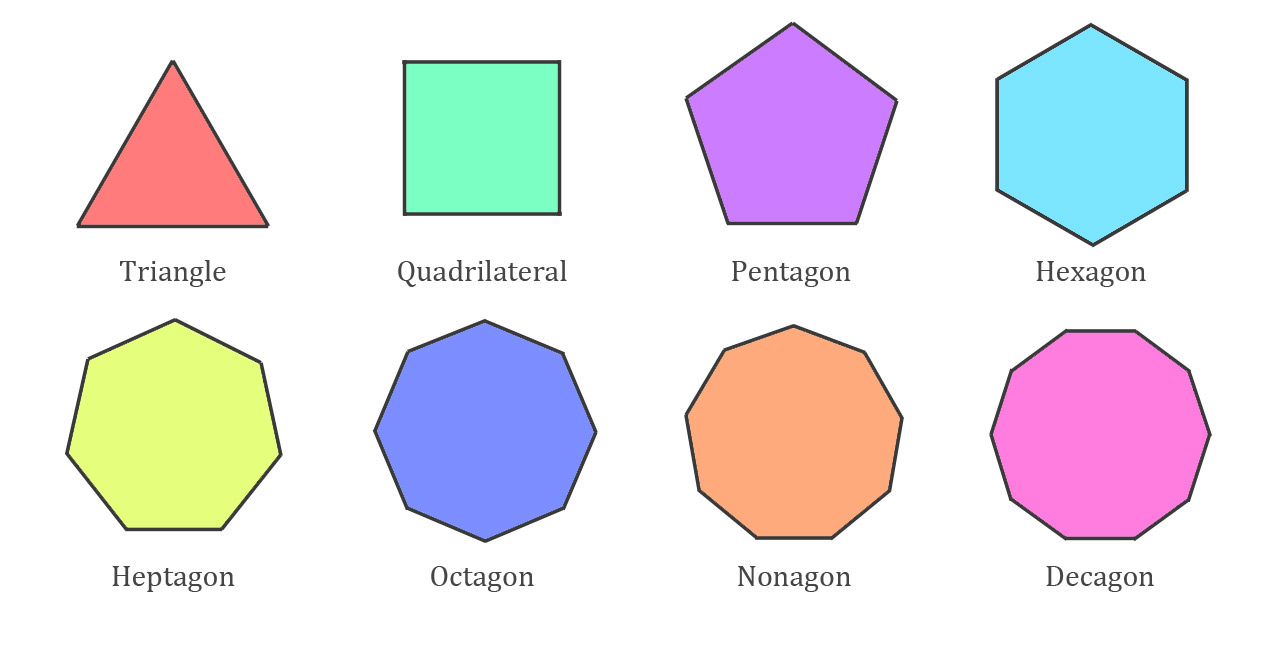
Regular vs. irregular polygons
If even one of those features is not present, you do not have a regular polygon. You may have three of the features (two dimensions; straight sides; an interior and exterior) but still not have a regular polygon. You would have an irregular polygon.
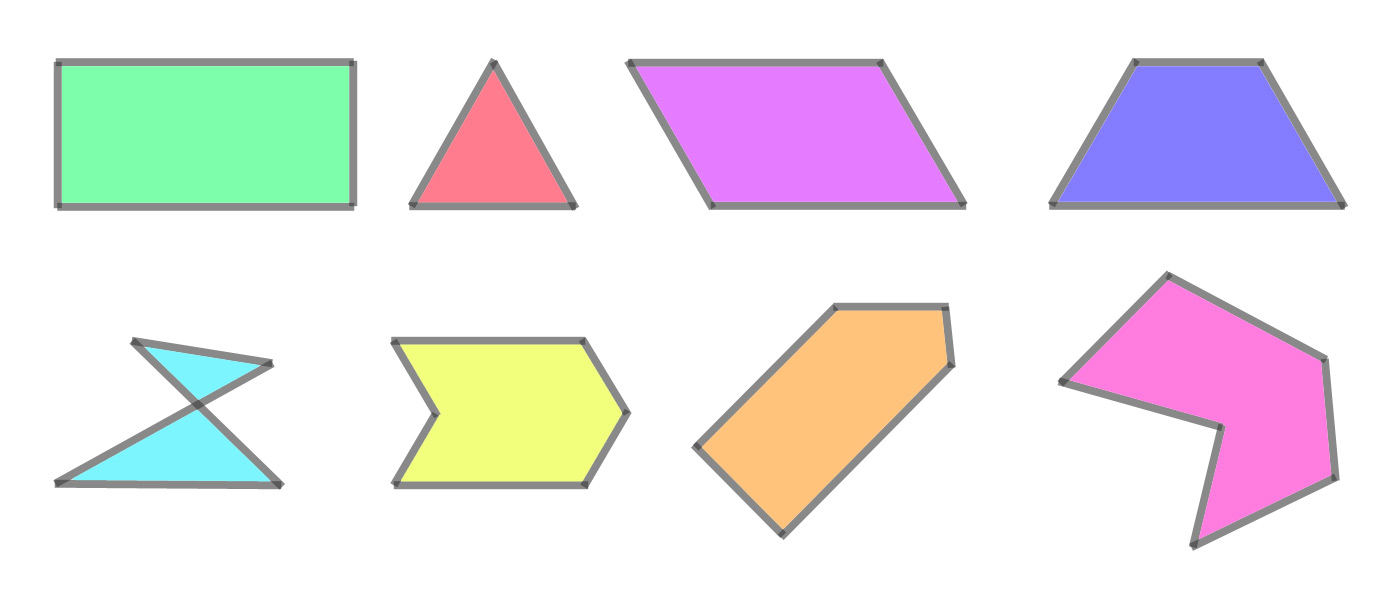
A rectangle that is longer than it is tall is an example of an irregular polygon. A scalene triangle, home plate on a baseball or softball field, and a kite are all also examples of irregular polygons.
Properties of regular polygons
Only when all six conditions, outlined above, are present will you have a regular polygon. Let's examine a suspicious shape and see:
Here we have △CAT, drawn with black lines. So our black CAT is suspicious, indeed.
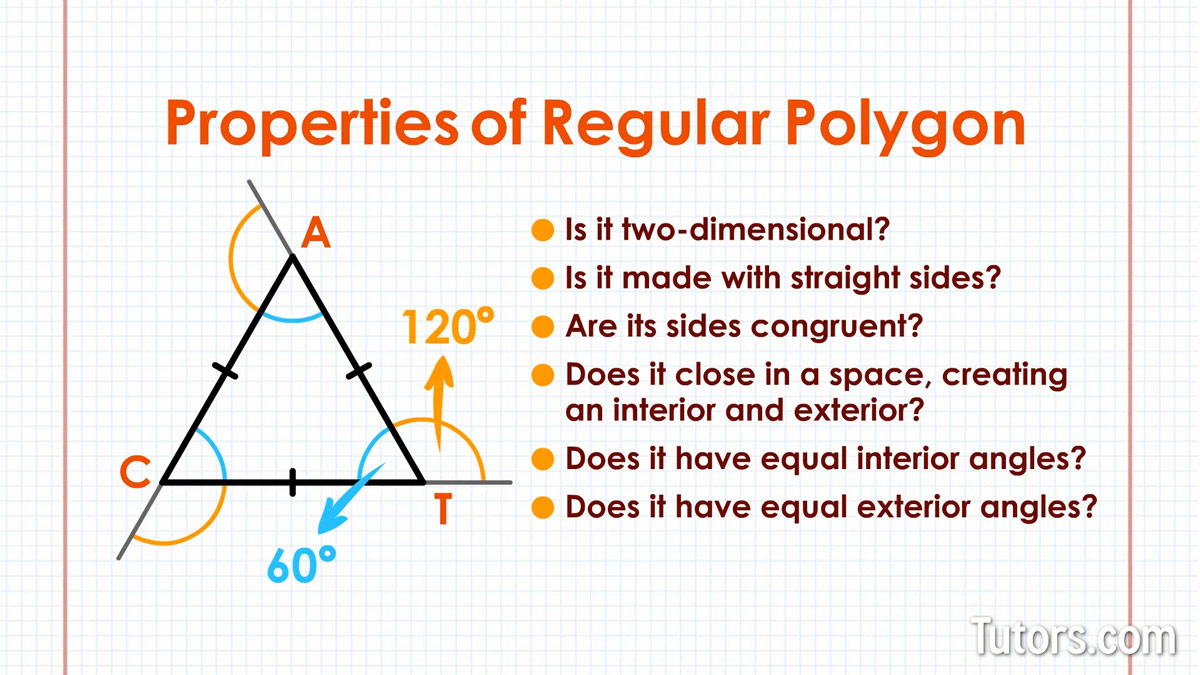
Go through the six properties of regular polygons:
Is it two-dimensional?
Is it made with straight sides?
Are its sides congruent?
Does it close in a space, creating an interior and exterior?
Does it have equal interior angles?
Does it have equal exterior angles?
Results of our scrutiny using the six identifying properties of regular polygons: △CAT is a regular polygon, the simplest kind. It is an equilateral triangle, with interior angles of 60° and exterior angles of 120°.
Names of regular polygons
Imagine you are unpacking a shipment of polygons. You have to put all the irregular polygons on the discount shelf, and all the regular polygons on the full-price shelf.
Using your knowledge of the identifying properties of regular polygons, you can easily see that only a few typical polygons are regular:
| Regular Polygon | Number of Sides | Interior Angles | Exterior Angles |
|---|---|---|---|
| Equilateral triangle | 3 sides | 3 interior angles of 60° | 3 exterior angles of 120° |
| Square | 4 sides | 4 interior angles of 90° | 4 exterior angles of 90° |
| Regular pentagon | 5 sides | 5 interior angles of 108° | 5 exterior angles of 72° |
| Regular hexagon | 6 sides | 6 interior angles of 120° | 6 exterior angles of 60° |
| Regular heptagon | 7 sides | 7 interior angles ≅ 128.57° | 7 exterior angles ≅ 51.43° |
| Regular octagon | 8 sides | 8 interior angles of 135° | 8 exterior angles of 45° |
How many sides does a regular polygon have?
You can create regular polygons of any number of sides and interior angles, but usually you will not name them with anything other than the number of their sides or interior angles and then -gon:
| Regular Polygon | Number of Sides | Interior Angles | Exterior Angles |
|---|---|---|---|
| Regular enneagon or 9-gon | 9 sides | 9 interior angles of 140° | 9 exterior angles of 40° |
| Regular decagon or 10-gon | 10 sides | 10 interior angles of 144° | 10 exterior angles of 36° |
| Regular hectogon or 100-gon | 100 sides | 100 interior angles of 176.4° | 100 exterior angles of 3.6° |
Any polygon that does not have equal-length sides along with equal interior and exterior angles is an irregular polygon; it goes on the discount shelf!
Parts of regular polygons
As simple as they are, regular polygons still have six parts:
Sides
Interior and exterior
Interior angles
Exterior angles
Vertices
Diagonals
We will illustrate with a basic regular polygon, the hexagon. This is a familiar shape (think of the cells of a honeybee hive):
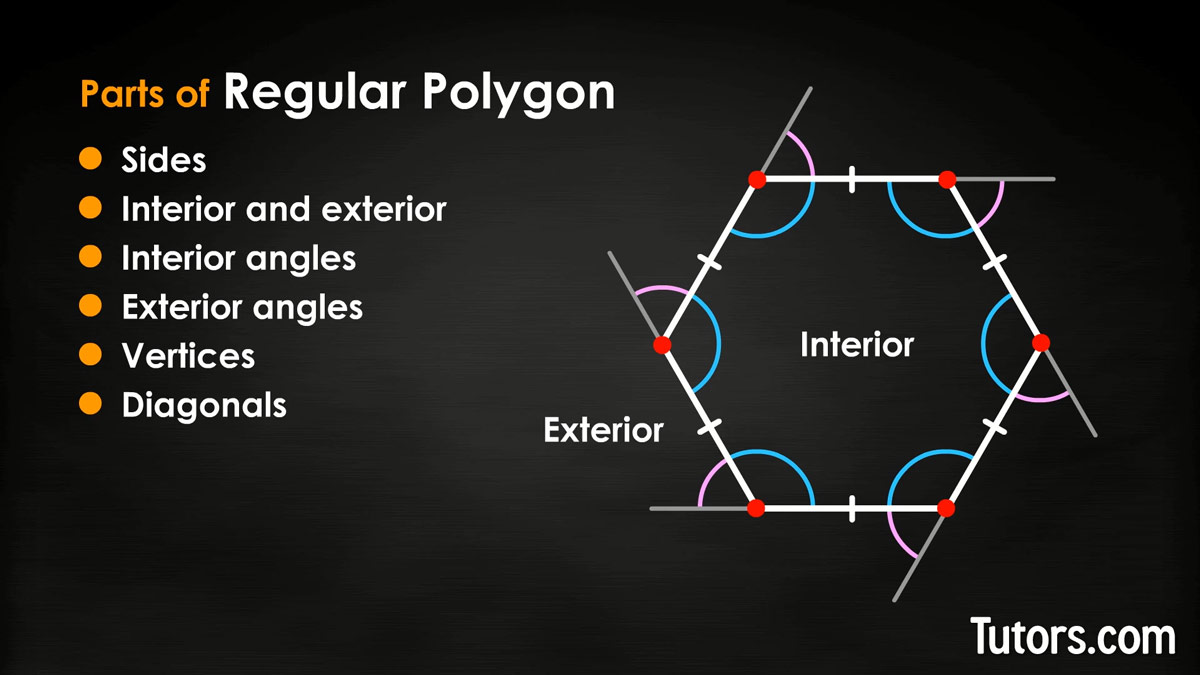
Our hexagon has six congruent sides. It has six equal interior angles, each 120°120°. It also has six equal exterior angles. An exterior angle is created by extending one side and measuring the angle between that extension and an adjacent side.
Regular polygon angles
Exterior angles of a regular polygon
Exterior angles of every simple polygon add up to 360°, because a trip around the polygon completes a rotation, or return to your starting place. Where sides meet, they form vertices, so our hexagon also has six vertices.
Interior angles of a regular polygon
Inside the hexagon's sides, where the interior angles are, is the hexagon's interior. Outside its sides is the hexagon's exterior. This becomes important when you consider complex polygons, like a star-shape (a pentagram, for example).
Diagonal of a polygon
Connect any non-adjacent vertices in the interior of the hexagon to make diagonals. All simple polygons can be divided into triangles using diagonals. The minimum number of triangles created in our hexagon, by drawing three diagonals, is four; each triangle has interior angles adding to 180°, so the sum of the interior angles of a regular hexagon is 4 × 180°, or 720°.
Regular polygon formula
The formula for calculating the sum of interior angles of any regular polygon with n sides is:
To find any single interior angle, divide your answer by n.
Lesson summary
Now you have all the tools you need to identify polygons, tell regular ones from irregular ones, name regular polygons and recognize them by their properties, list the parts of regular polygons (sides, interior, interior angles, vertices, diagonals, exterior angles), and calculate the sums of the interior angles of polygons.
What you learned:
After viewing the video and studying the drawings, please read the entire lesson. Then you will learn to:
Identify polygons
Identify regular and irregular polygons
State the identifying properties of regular polygons
Name examples of regular polygons
List six parts of regular polygons
Calculate the sum of interior angles of regular polygons