20+ tutors near you & online ready to help.

TABLE OF CONTENTS

Triangular Pyramid — How To Find Volume & Surface Area (Formulas)

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Triangular pyramid

A triangular pyramid is a three-dimensional solid – a polyhedron – with a triangular base and three triangular faces meeting at the pyramid’s apex.

The base of a pyramid can be any two-dimensional geometric shape:

Triangle
Rectangle
Square
Hexagon
Octagon

There are many types of pyramids, and all pyramids are named by the shape of their bases.

Just as you can have a triangular pyramid, you can also have a rectangular pyramid, a pentagonal pyramid, etc.

The Great Pyramids of Egypt in Giza, for example, is a square pyramid because its base (bottom) is a square. A triangular pyramid is a pyramid with a triangular base.

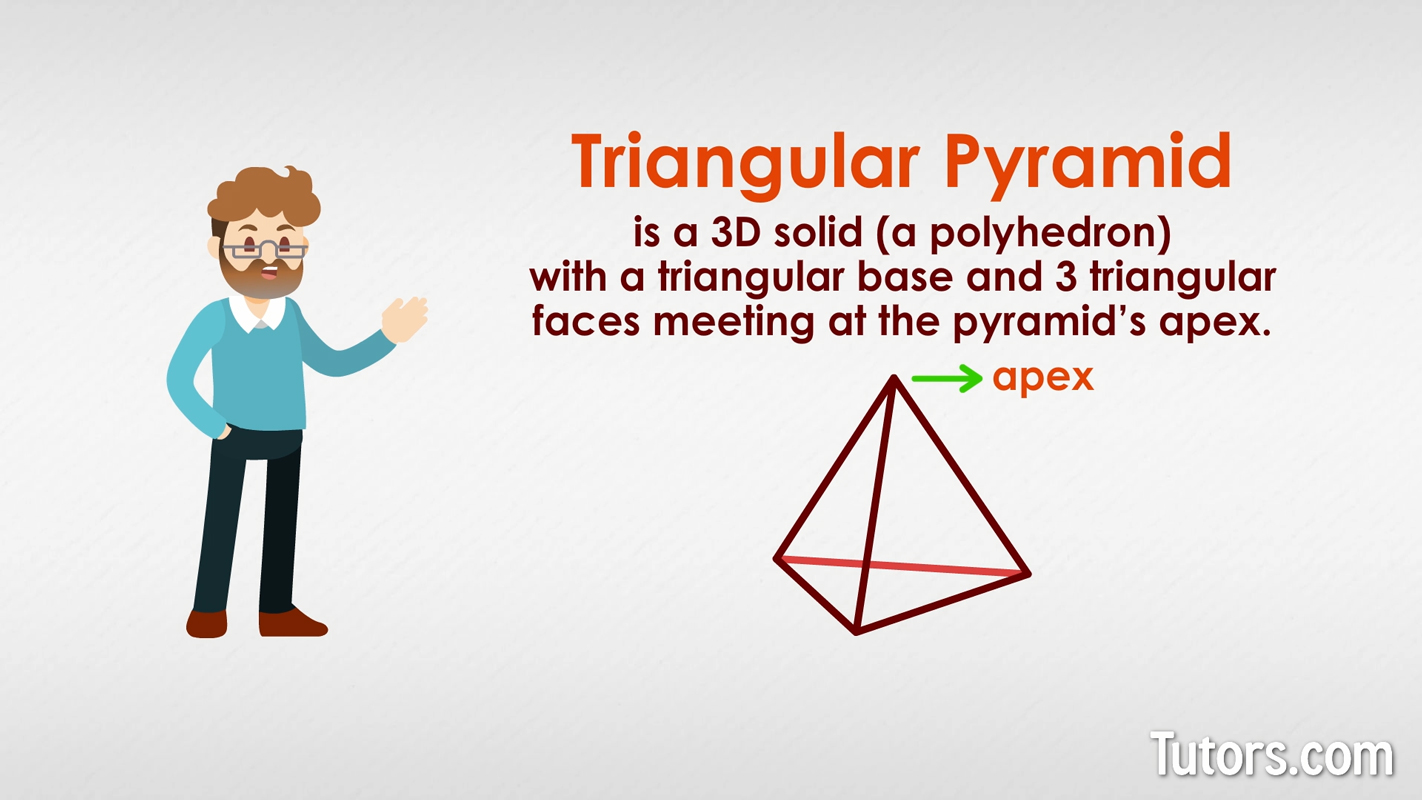
Triangular pyramid faces, edges, and vertices

A triangular pyramid has:

Triangular base
3 triangular faces
6 edges
4 vertices

Triangular pyramid - faces, edges, and vertices

Regular triangular pyramid

A pyramid with an equilateral triangle base is a regular triangular pyramid. If a scalene or isosceles triangle forms the base, then the pyramid is a non-regular triangular pyramid.

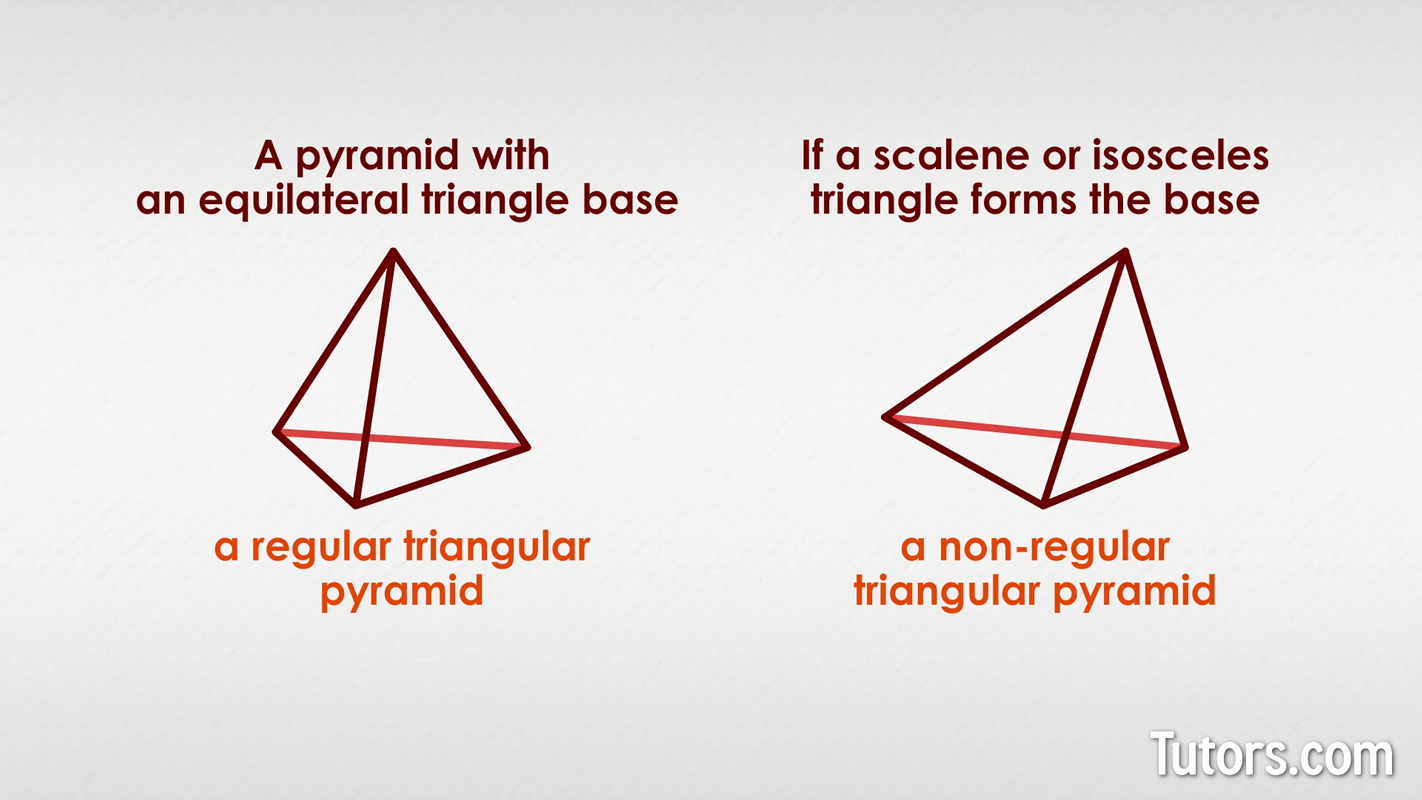
No rule requires the base of a triangular pyramid to be an equilateral triangle, though constructing scalene or isosceles triangular pyramids is far harder than constructing an equilateral triangular pyramid.

Get free estimates from geometry tutors near you.

Surface area of a triangular pyramid

Two different surface area measurements can be taken for any 3D solid: the lateral surface area and the surface area.

Lateral surface area, LSA, does not include the base for our pyramid. The surface area of a pyramid, SA, includes the base.

The surface area of a triangular pyramid with three congruent, visible faces is the area of those three triangular faces, plus the area of the triangular base.

The formula for calculating the surface area involves the area of the base, the perimeter of the base, and the slant height of any side.

Surface area of a triangular pyramid formula

SA=Base Area+\frac{1}{2}(Perimeter\times Slant Height)

This formula works because you are adding the base area to the area of all three slanted faces. The perimeter gives you the sum of all three bases. You multiply that sum times the slant height of the triangular pyramid as though you had one big rectangle, and then you take one-half of that as the area of the three triangles.

How to find the surface area of a triangular pyramid

Suppose you have this triangular pyramid:

Surface area formula of a triangular pyramid

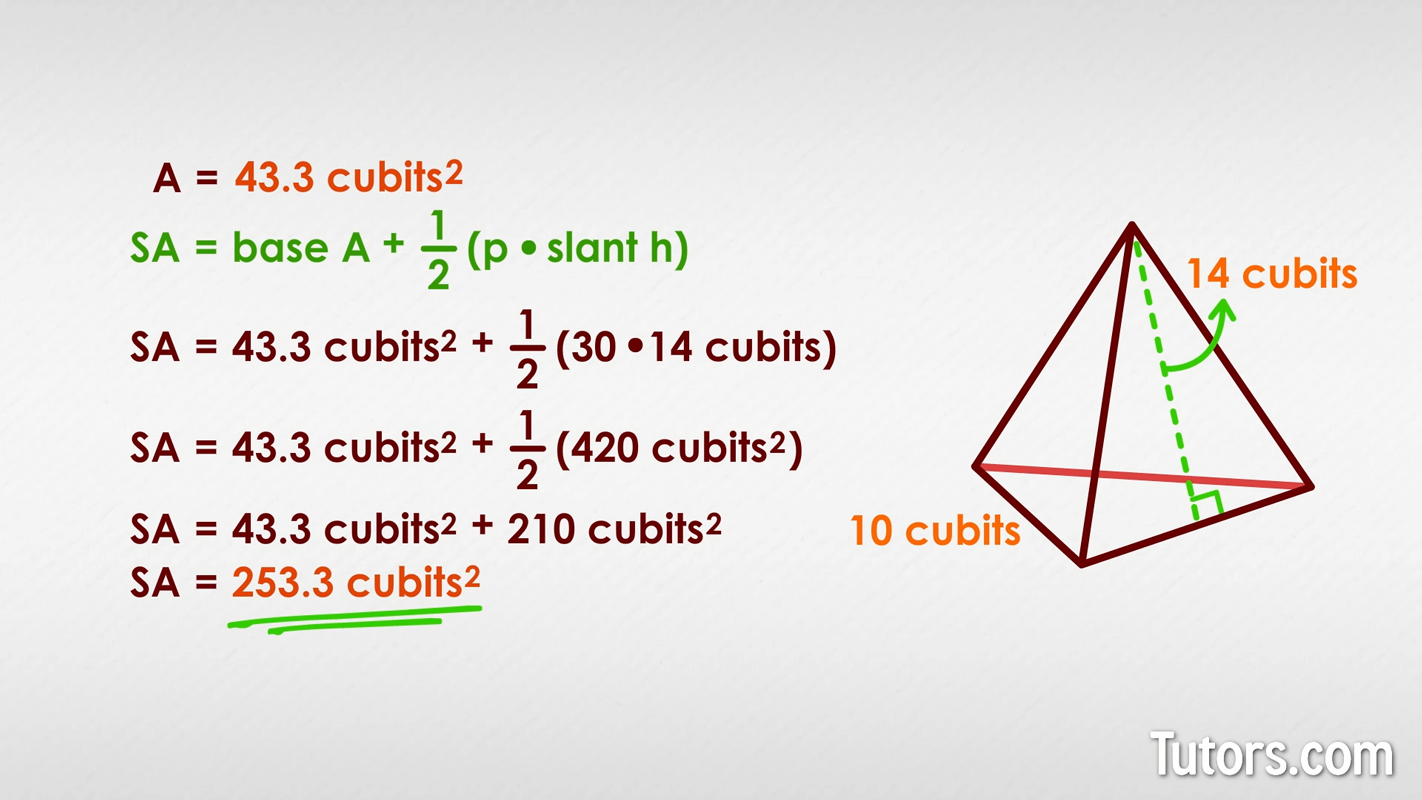
The base of the pyramid is an equilateral triangle since all three of its sides are 10 cubits. To find the area of the base triangle, use this formula for the area of an equilateral triangle with sides a:

A=\frac{\sqrt{3}}{4}{a}^{2}

For this particular triangular pyramid, the formula works out as:

A=\frac{\sqrt{3}}{4}{10}^{2}\approx \mathbf{43.3}\mathit{c}\mathit{u}\mathit{b}\mathit{i}\mathit{t}{\mathit{s}}^{\mathbf{2}}

We have now found the area of the base. We already know the perimeter of the base is 30 cubits (the three sides are each 10 cubits), and we are given the slant height, 14 cubits.

SA=43.3cubit{s}^{2}+\frac{1}{2}\left(30cubits\times 14cubits\right)

SA=43.3cubit{s}^{2}+\frac{1}{2}\left(420cubit{s}^{2}\right)

SA=43.3cubit{s}^{2}+210cubit{s}^{2}

SA=253.3cubit{s}^{2}

Area is always measured in square units, whether they are $c{m}^{2}$ , ${m}^{2}$ , $f{t}^{2}$ , or $cubit{s}^{2}$ .

How to calculate lateral surface area of a triangular pyramid

You may have needed to take your time getting through all that, finding the area of the base, finding the perimeter, adding everything.

To find the area of just the slanted sides – the lateral surface area (LSA) – you need to do a lot less work:

LSA=\frac{1}{2}(Perimeter\times Slant Height)

Lateral surface area formula for a triangular pyramid

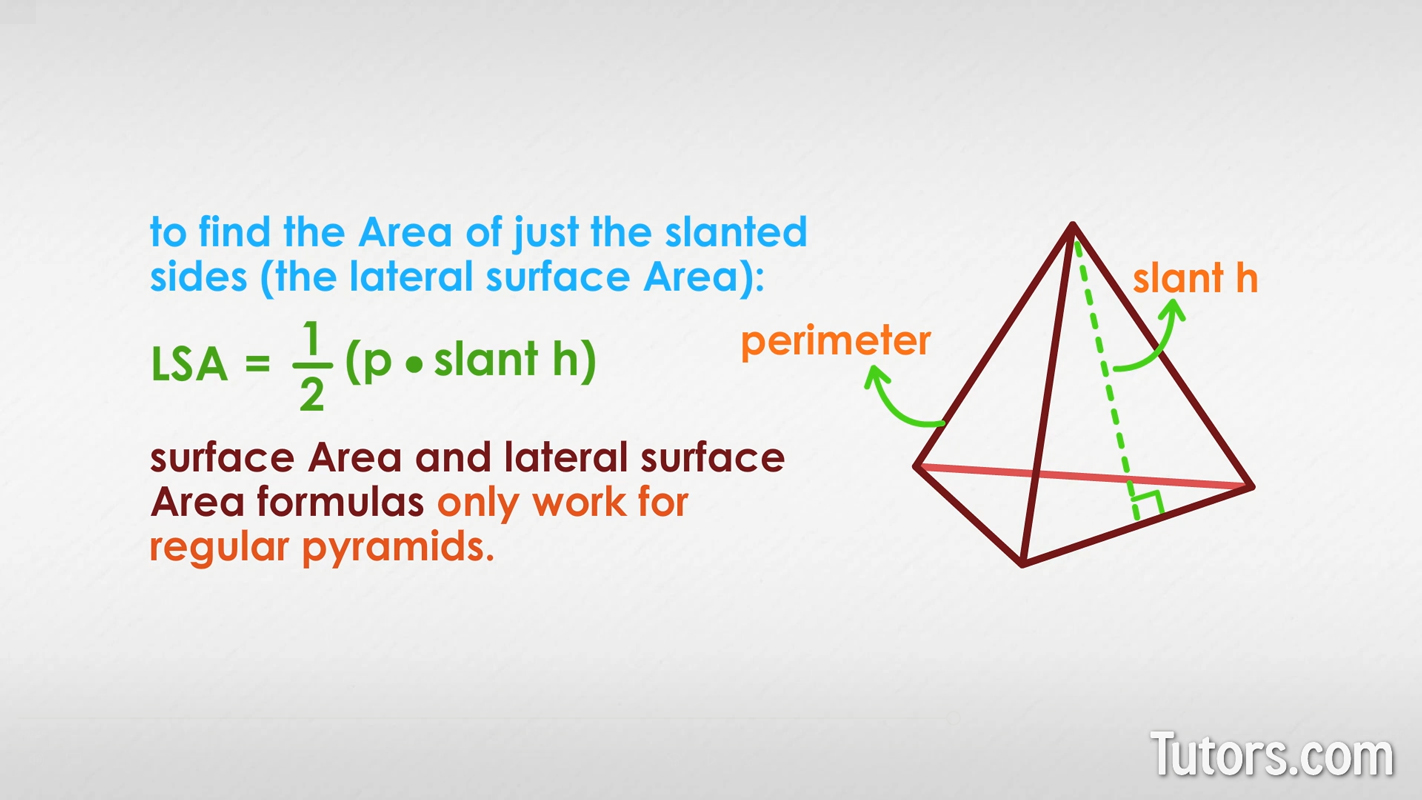
These formulas only work for regular pyramids. If you have a non-regular triangular pyramid, calculate the area of each of the four faces individually (three slanted faces and the base) and add them together.

Volume of a triangular pyramid

Volume is the amount of space a 3D solid takes up, so, with a triangular pyramid, we are finding how much room it has inside it. It is always measured in cubic units. Though the pyramid rapidly diminishes to an apex, the calculation is not hard.

Triangular pyramid volume formula

V=\frac{1}{3}Ah

In the volume of a triangular pyramid formula, A is the area of the base and h is the height from base to apex.

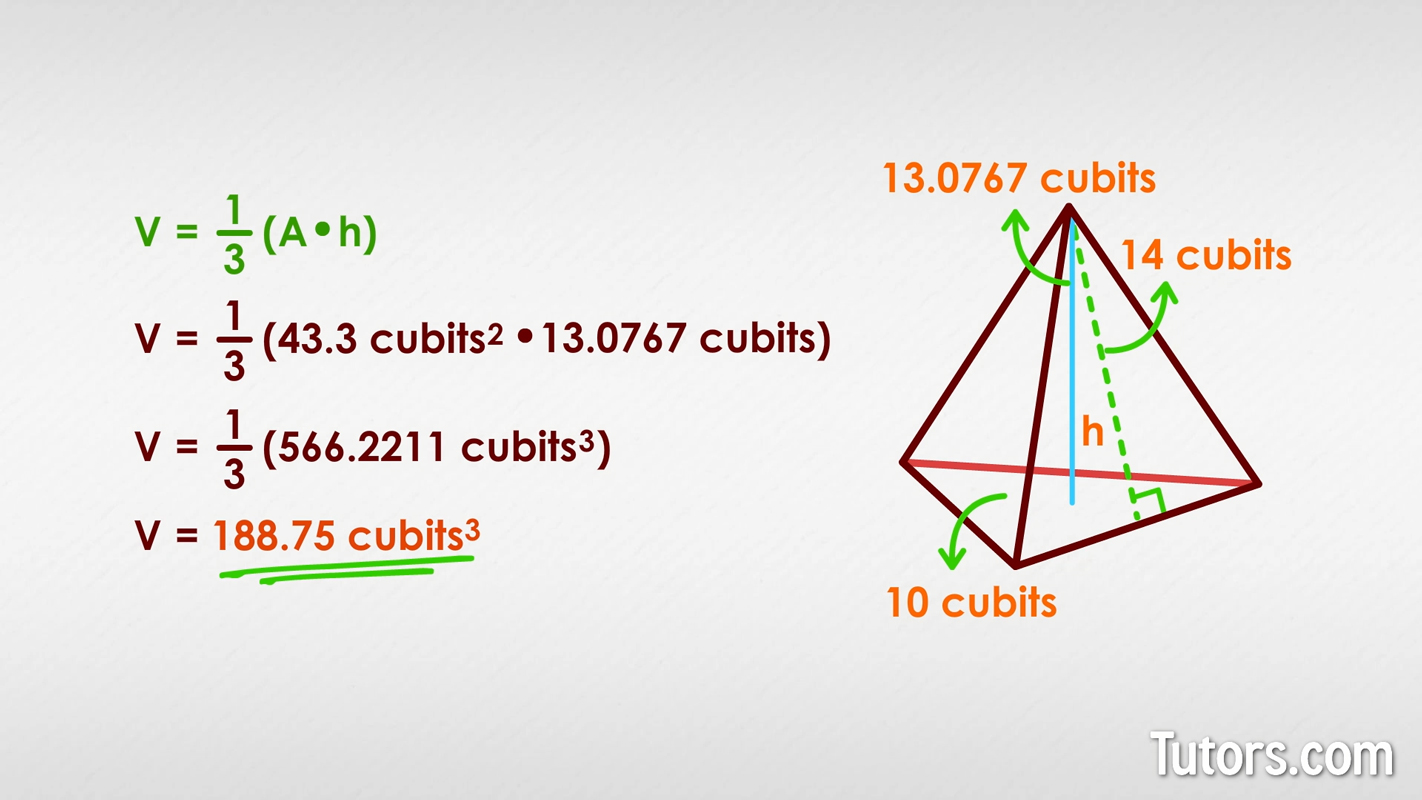
For our pyramid with a base 10 cubits and slant height of 14 cubits, the height, h, works out to 13.0767 cubits. We already know the area from our earlier calculations, so we can plug the know numbers in to get the volume in cubic cubits:

V=\frac{1}{3}Ah

V=\frac{1}{3}(43.3cubit{s}^{2}\times 13.0767cubits)

V=\frac{1}{3}(566.2211cubit{s}^{3})

V\approx 188.75\cubit{s}^{3}

Please note that, with the fraction as a factor in our multiplication, we do not have a precise decimal answer, so we have an approximate value.