The 5 Platonic Solids Explained — Definition And Types
What is a Platonic solid?
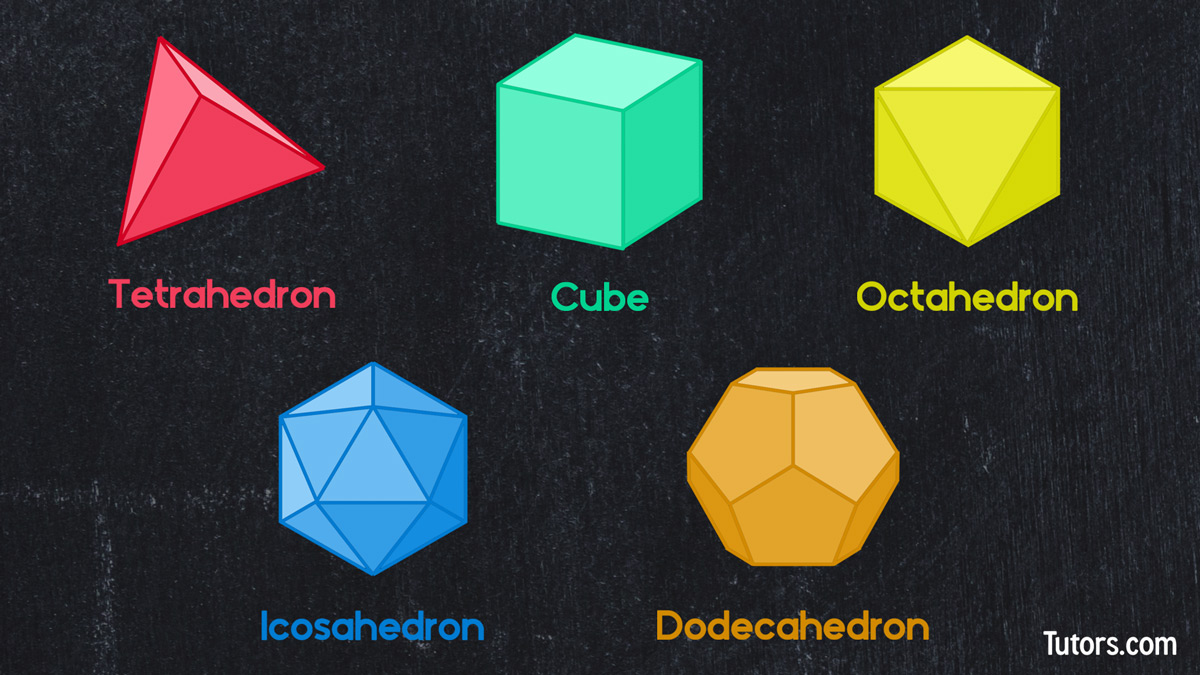
A Platonic solid is a regular, convex polyhedron in a three-dimensional space with equivalent faces composed of congruent convex regular polygonal faces. The five solids that meet this criterion are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
Some sets in geometry are infinite, like the set of all points in a line. Platonic solids, however, are a finite set of only five, three-dimensional shapes. No matter which way you look at a Platonic solid, the same-shape face stares back.
Properties of Platonic solids
To be a Platonic solid, the tested shape must:
Be convex
Be three-dimensional (a polyhedron)
Have congruent faces
Have congruent corners (vertices)
History of the 5 Platonic solids
Greek philosopher Plato used the already existing concept of five perfect solids to connect the flawed, real world to the ideal world of his imagination. Because the five solids each present the same face no matter how they are rotated, Plato used them in his dialogue Timaeus around 350 BCE. He assigned four shapes to elements (fire, earth, water, air) and the dodecahedron to the heavens. He had organized the known universe; the solids were then always known as Platonic solids in his honor.
The five Platonic solids
Here are the five Platonic Solids and their relationships to two-dimensional shapes:
Tetrahedron has four triangular faces
Cube has six square faces
Octahedron has eight triangular faces
Dodecahedron has 12 pentagonal faces
Icosahedron has 20 triangular faces
No other shapes can be created by repeating only a two-dimensional regular polygon. Three of the five solids depend on the simplicity of the equilateral triangle. Also, notice that the number of faces of all the Platonic solids is even.
Another exciting feature of Platonic solids: their faces meet so that either three, four, or five faces join at vertices to form corners:
Tetrahedron has four vertices with three triangular faces meeting
Cube has eight vertices with three square faces meeting
Octahedron has six vertices with four triangular faces meeting
Dodecahedron has 20 vertices with three pentagonal faces meeting
Icosahedron has 12 vertices with five triangular faces meeting
Tetrahedron
From the Greek, meaning four-sided or four-faced, this shape is four equilateral triangles joined along six edges to form four vertices or corners. It makes for a sturdy pyramid. Among the Platonic solids, only the tetrahedron has no faces parallel to one another.

Cube
From the Greek, meaning a six-sided die, the cube is six squares joined along 12 edges to form eight vertices. It is ubiquitous in our modern society and known to humans for thousands of years. Cubes have three pairs of parallel faces.

Octahedron
From the Greek, eight-faced or eight-sided, the octahedron is eight equilateral triangles joined along 12 edges to make six vertices or corners. The shape has four pairs of parallel faces.

Dodecahedron
From the Greek, meaning twelve-faced, the dodecahedron has 12 faces formed from pentagons. These join along 30 edges to form 20 vertices. As a result, this shape is the second-most "rounded" of the Platonic solids. It has six pairs of parallel faces.

Icosahedron
From the Greek, meaning 20-faced, the icosahedron has 20 equilateral triangles joined along 30 edges to form 12 vertices. Because of its relatively shallow angles, it most closely approximates a sphere among the Platonic solids. It has ten pairs of parallel faces.

Uses of Platonic solids
Because Platonic solids relate so well to numbers, their shapes often appear as dice in board games and other recreations, including gambling. The cube, of course, appears as sugar cubes, shipping boxes, ice cubes, and anywhere an easily packed, easily repeated shape is needed.
Minerals often form rough approximations of Platonic solids:
Tetrahedron: Tetrahedrite
Cube: Halite, Pyrite, Galena
Dodecahedron: Garnet
Octahedron: Fluorite, Spinel, Diamond
Amazingly, molecular structures also mimic some of the Platonic solids, either naturally or through human-made chemical compounds:
Tetra-tert-butyltetrahedrane
Cubane
Dodecahedrane
Even the microscopic world has examples of Platonic solids. Viruses, some of the smallest possible forms of life, make use of the icosahedron and the cube to optimize its life functions. The dual discoverers of DNA, Watson and Crick, predicted such icosahedral and cubic symmetry in their work.
Lesson summary
Now that you have worked through this lesson, you can identify and name the five Platonic solids, state the identifying characteristics of the five Platonic solids, and relate the five Platonic solids to their real-life approximations.