Tangent of a Circle — Definition & Formula
Tangent to a circle
A tangent to a circle is a straight line that touches the circle at one point, called the point of tangency. At the point of tangency, the tangent of the circle is perpendicular to the radius.
Here we have circle A where is the radius and is the tangent to the circle.
This means that is perpendicular to .
Let's try an example where and . How do we find the length of ?
The angle T is a right angle because the radius is perpendicular to the tangent at the point of tangency, .
This means we can use the Pythagorean theorem to solve for .
Circles
Circles are the set of all points a given distance from a point. This means a circle is not all the space inside it; it is the curved line around a point that closes in a space. A circle has a center, which is that point in the middle and provides the name of the circle. A circle can have a:
radius (the distance from the center to the circle)
chord (a line segment from the circle to another point on the circle without going through the center)
secant (a line passing through two points of the circle)
diameter (a chord passing through the center)
circumference (the distance around the circle itself.
Here is a crop circle that shows the flattened crop, a center point, a radius, a secant, a chord, and a diameter:
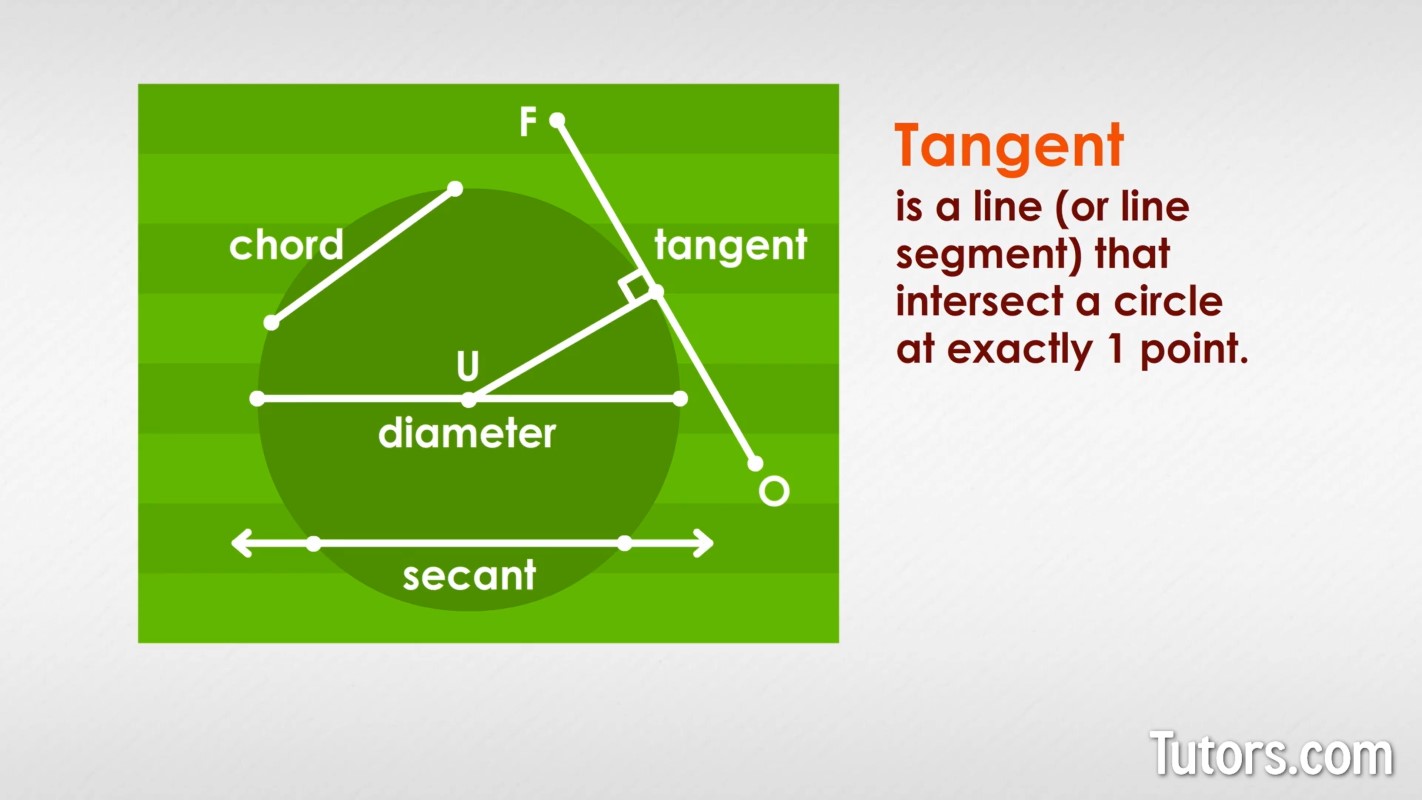
Notice that the diameter connects with the center point and two points on the circle. A chord and a secant connect only two points on the circle. A tangent connects with only one point on a circle.
What is a tangent?
A tangent is a line (or line segment) that intersects a circle at exactly one point. To do that, the tangent must also be at a right angle to a radius (or diameter) that intersects that same point.
In our crop circle U, if we look carefully, we can see a tangent line off to the right, line segment FO. That would be the tiny trail the circle makers walked along to get to the spot in the field where they started forming their crop circle. Crop circles almost always "appear" very close to roads and show some signs of tangents, which is why most researchers say they are made by human pranksters.
The word "tangent" comes from a Latin term meaning "to touch," because a tangent just barely touches a circle. Tangents, of course, also allude to writing or speaking that diverges from the topic, as when a writer goes off on a tangent and points out that most farmers do not like having their crops stomped down by vandals from this or any other world.
Tangent line circle
Lines and line segments are not the only geometric figures that can form tangents. One circle can be tangent to another, simply by sharing a single point. The two circles could be nested (one inside the other) or adjacent, like this:
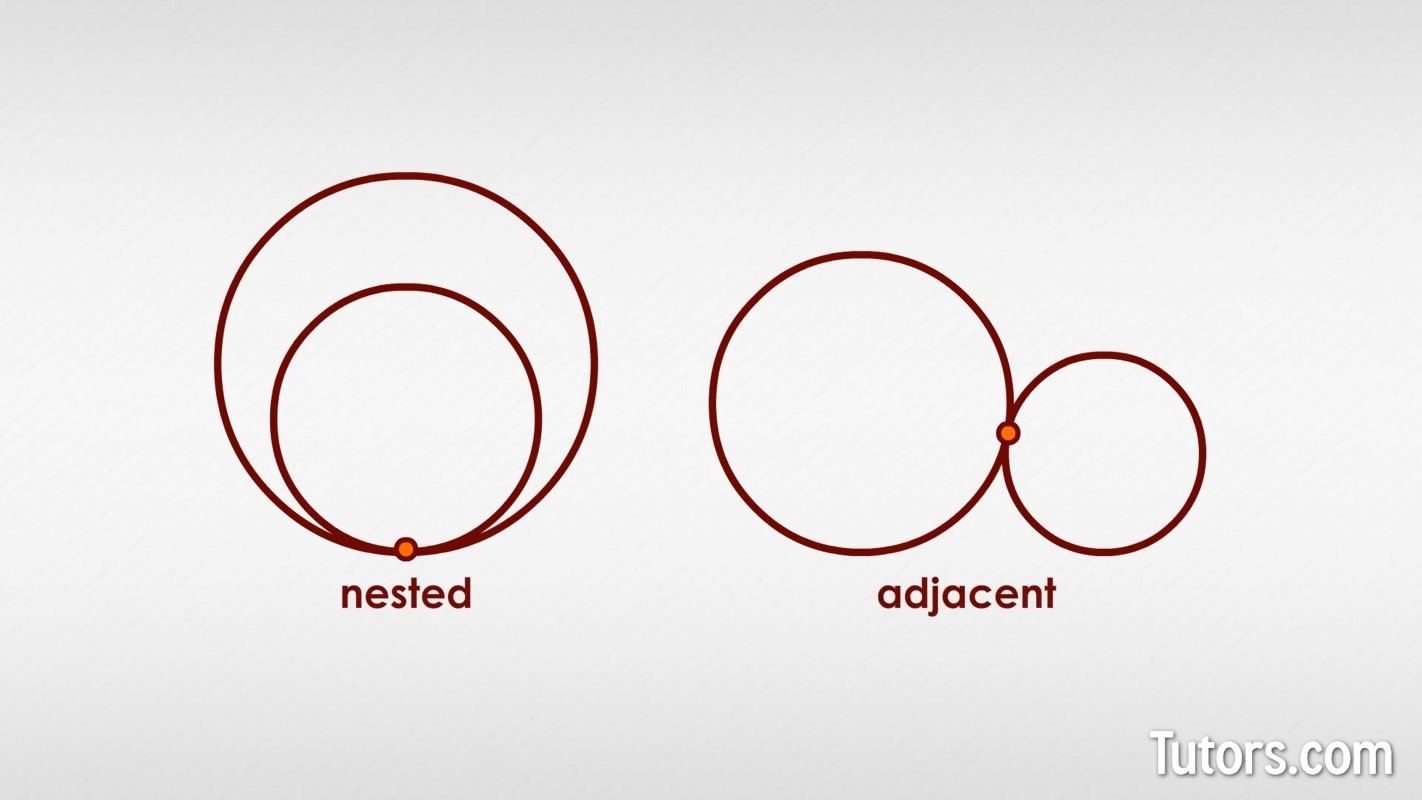
You can also surround your first crop circle with six circles of the same diameter as the first. This forms a crop circle nest of seven circles, with each outer circle touching exactly three other circles, and the original center circle touching exactly six circles:

Tangent of a circle theorem
Three theorems (that do not, alas, explain crop circles) are connected to tangents. We already snuck one past you, like so many crop circle makers skulking along a tangent path: a tangent is perpendicular to a radius.
The second theorem is called the Two Tangent Theorem. It states that, if two tangents of the same circle are drawn from a common point outside the circle, the two tangents are congruent.
The Tangent Secant Theorem explains a relationship between a tangent and a secant of the same circle.
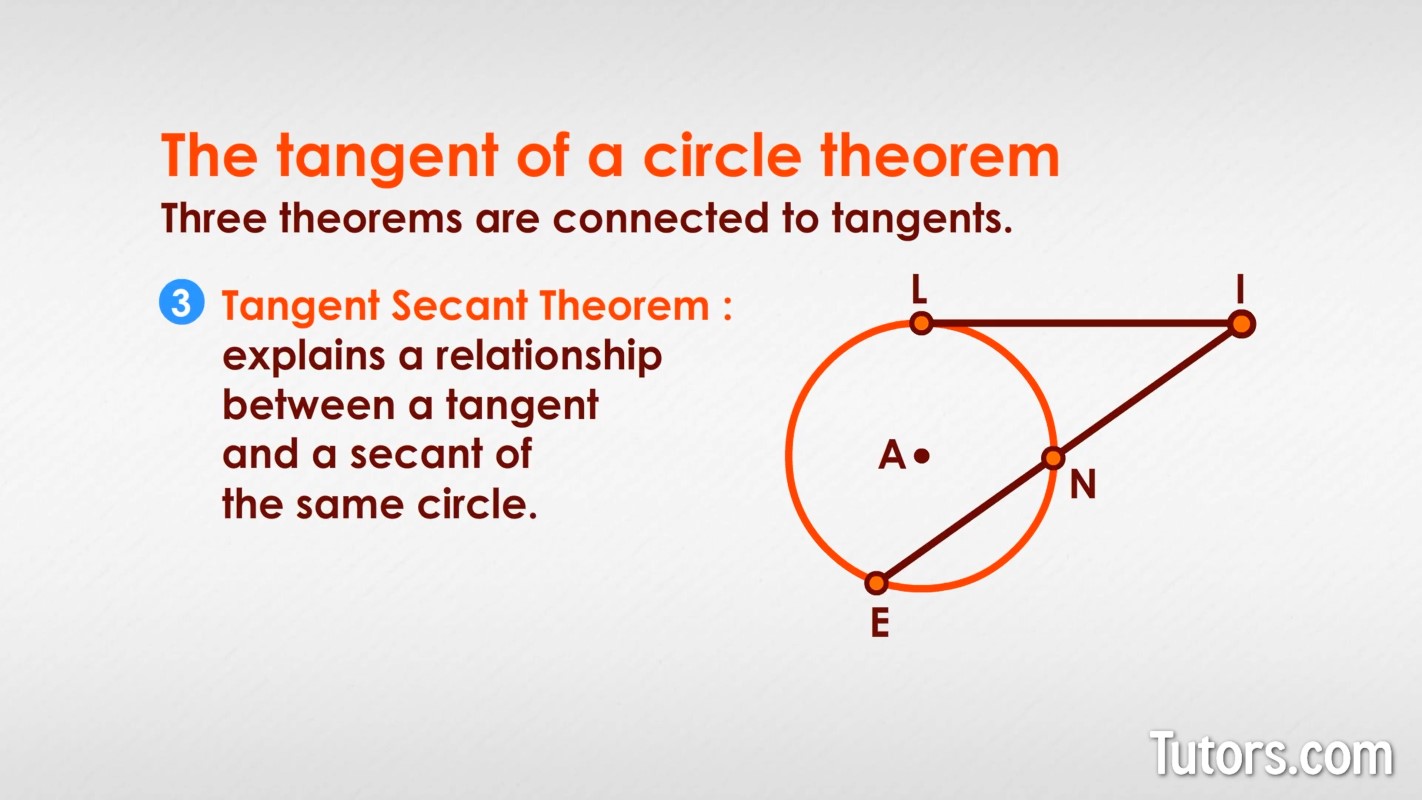
With Point I common to both tangent LI and secant EN, we can establish the following equation:
Though it may sound like the sorcery of aliens, that formula means the square of the length of the tangent segment is equal to the product of the secant length beyond the circle times the length of the whole secant.
Lesson summary
Though we may not have solved the mystery of crop circles, you now are able to identify the parts of a circle, identify and recognize a tangent of a circle, demonstrate how circles can be tangent to other circles, and recall and explain three theorems related to tangents of circles.