Radius, Diameter, & Circumference of a Circle
What is a circle?
In mathematics, a circle is the set of all coplanar points equidistant from a given point. That given point is the circle's center, and it does not lie on the circle. The circle is only the set of points (forming a curved line returning back on itself) that are in the same plane and the same distance from a center point, the center of a circle.
The circle itself is not the inside space, the center point, or space outside of the circle. The circle is the line that circles back onto itself.
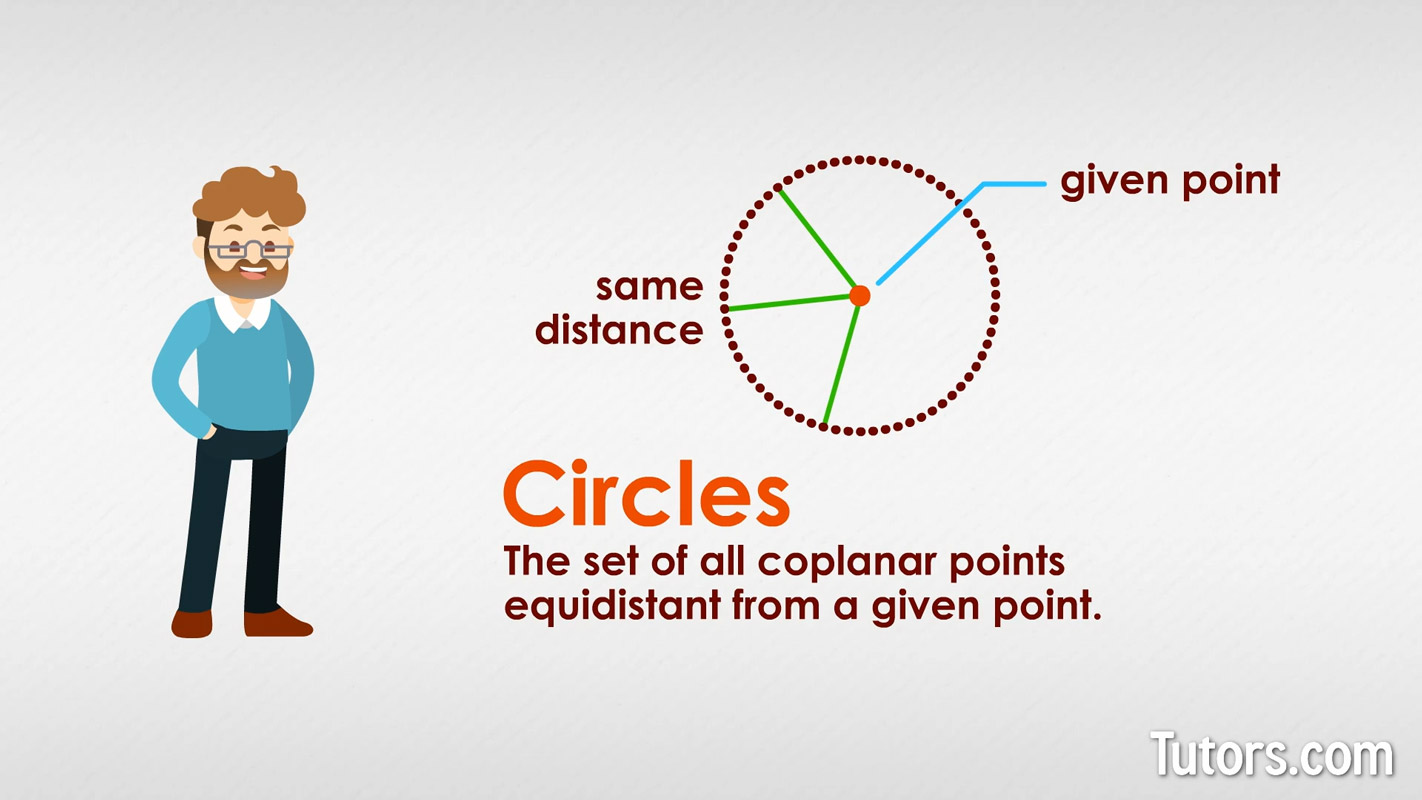
Without its identifying center point, the circle is nameless. The center of the circle is how the circle is named, so take the circle and place Point I in the middle, and now we have Circle I.
Radius of a circle
To get from the center point to the actual circle, we move in a straight line called a radius. Radius is the measure of that distance. The radius of a circle is one way to measure the size of the circle. Radius is always indicated by the small letter r.
Here is a line segment, IE, with endpoint II at the circle's center and endpoint E on the circle itself:
Radius formula
Radius is the diameter. Here is the radius formula:
Diameter of a circle
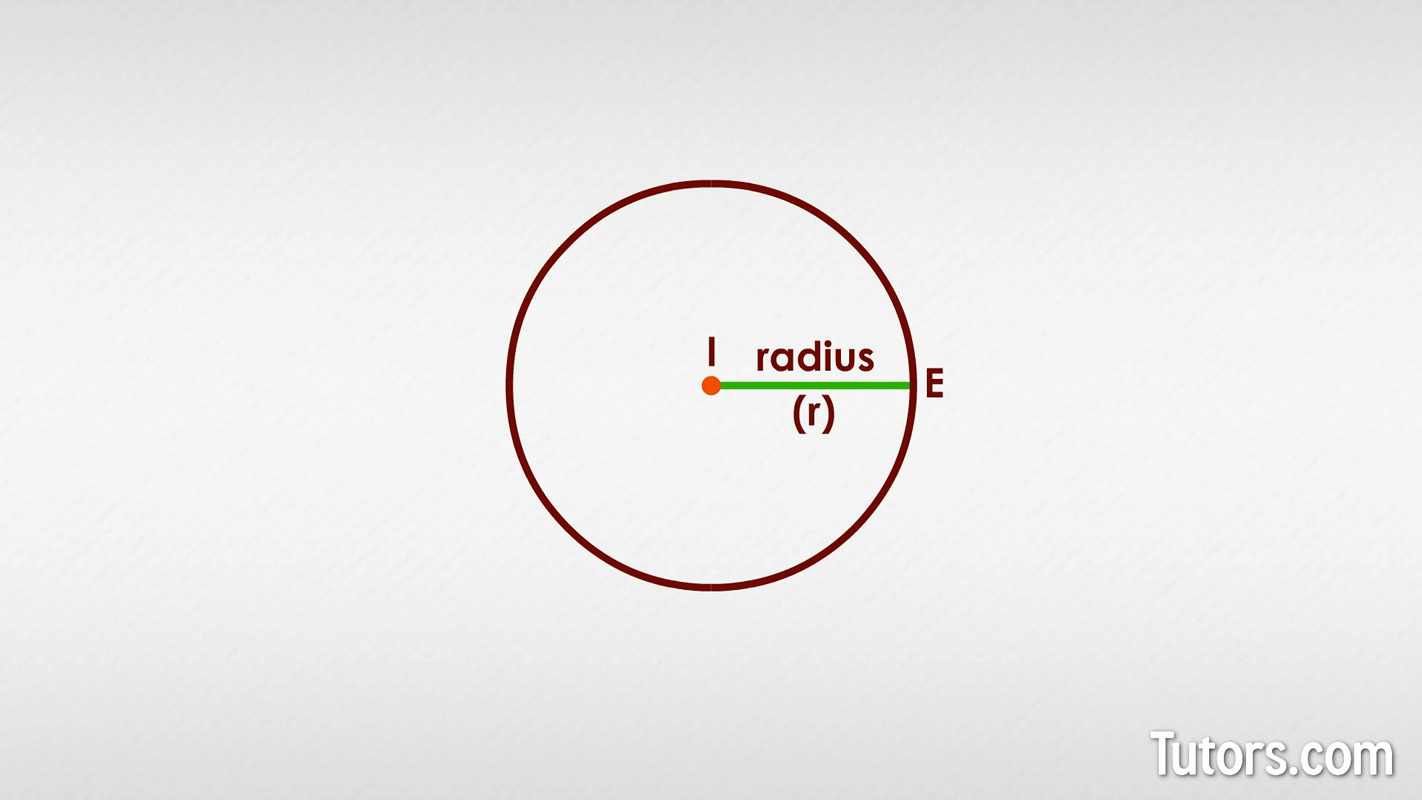
If we have two radii together, they can form central angles or a straight line across the circle. A straight line starting on the circle, passing through the center, and reaching to the circle again is a diameter.
Here is a diameter for Circle 2, built by extending radius IE in the other direction, to point P:
Instead of identifying that as two separate radii (the plural of radius), we can simply call PE a diameter of a circle. It is the distance across the entire circle. The diameter of the circle is always indicated by the lowercase letter d.
Diameter formula
This means the diameter is 2 times the radius of the circle. Here is the diameter formula:
Circles show up everywhere, like pizza at dinner!
Circumference of a circle
For polygons, the perimeter is the sum of the lengths of their sides. Circles have a perimeter, too, but we give it a special word: circumference (from Latin, to carry around). The circumference of a circle is the distance around the circle.
Let's take a look at the ratio of the circumference to diameter in these circles below. Here is Circle 1 with a diameter of 1 meter and Circle 2 with a diameter of 2 meters:

The distance all the way around Circle 1, the circumference of the circle, is 3.1415926 meters.
The circumference of Circle 2 is 6.2831852 meters.
Set up each circle's circumference to its diameter. These form ratios. See anything?
The ratio of the circumference C to diameter dd of both circles simplify to the same value, 3.1415926!
The ratio of the circumference, C, of any circle to its diameter dd is always the same value, 3.1415926, named using the Greek letter pi (as in apple pie), which looks like this: π.
When using pi, it is acceptable to round to two decimal places.
Circumference formula
Now we can substitute π instead of that long number and show a formula of the circumference (C) and diameter (d). When we multiply both sides of the formula by (d) we get:
Now we can find the circumference (C) of any circle as long as we know the diameter (d). If you have the radius, you can still find the circumference of a circle, since the radius is equal to half the diameter:
How to find the circumference of a circle
Let's try a practice problem and find the circumference of a circle that has a diameter of 20.
Start by plugging in 20 for our diameter (d) in our formula:
You did it! We can leave our answer in terms of ππ, so the circumference of the circle is 20π units.
Circumference parts
There are more parts to a circle left to cover. Imagine you sit down to a delicious, hot pizza, but it is not cut! You cut away a single slice, like this:
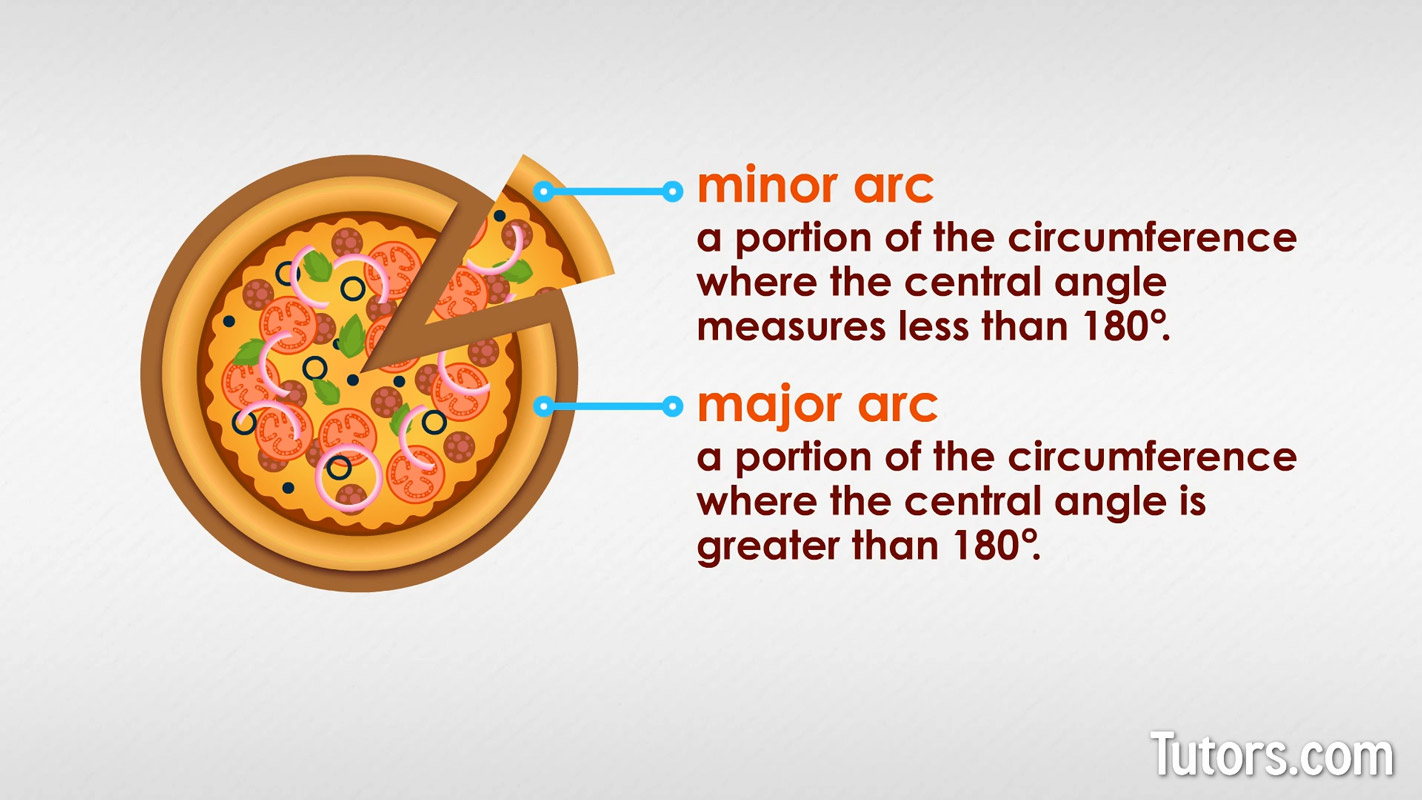
The portion of the crust in the cut piece is much smaller than the rest of the crust. That smaller portion is the minor arc of the circle. The larger part, the remaining circumference, is the major arc.
A minor arc is a portion of the circumference where the central angle measures less than 180°. A major arc is a portion of the circumference where the central angle is greater than 180°.