Parallel Sides & Parallel Shapes

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Parallel sides definition

Parallel sides are two sides of a shape that are always the same distance apart and never meet. If we continue two parallel sides of a shape out infinitely making them parallel lines, they will always be the same distance apart.

Parallel shapes

We know that many types of quadrilaterals, such as the trapezoids, a rhombus, rectangles, and all the regular polygons (except for the triangle), have parallel sides. One other shape has parallel sides: the parallelogram.

The parallelogram is a special type of quadrilateral. It is named for its property of having two pairs of parallel sides (left and right, top and bottom) but no other limitation.

Polygons with parallel sides could have one pair of parallel sides like an isosceles trapezoid, two pairs of parallel sides like this square and rectangle, or even four pairs of parallel sides like a regular octagon:

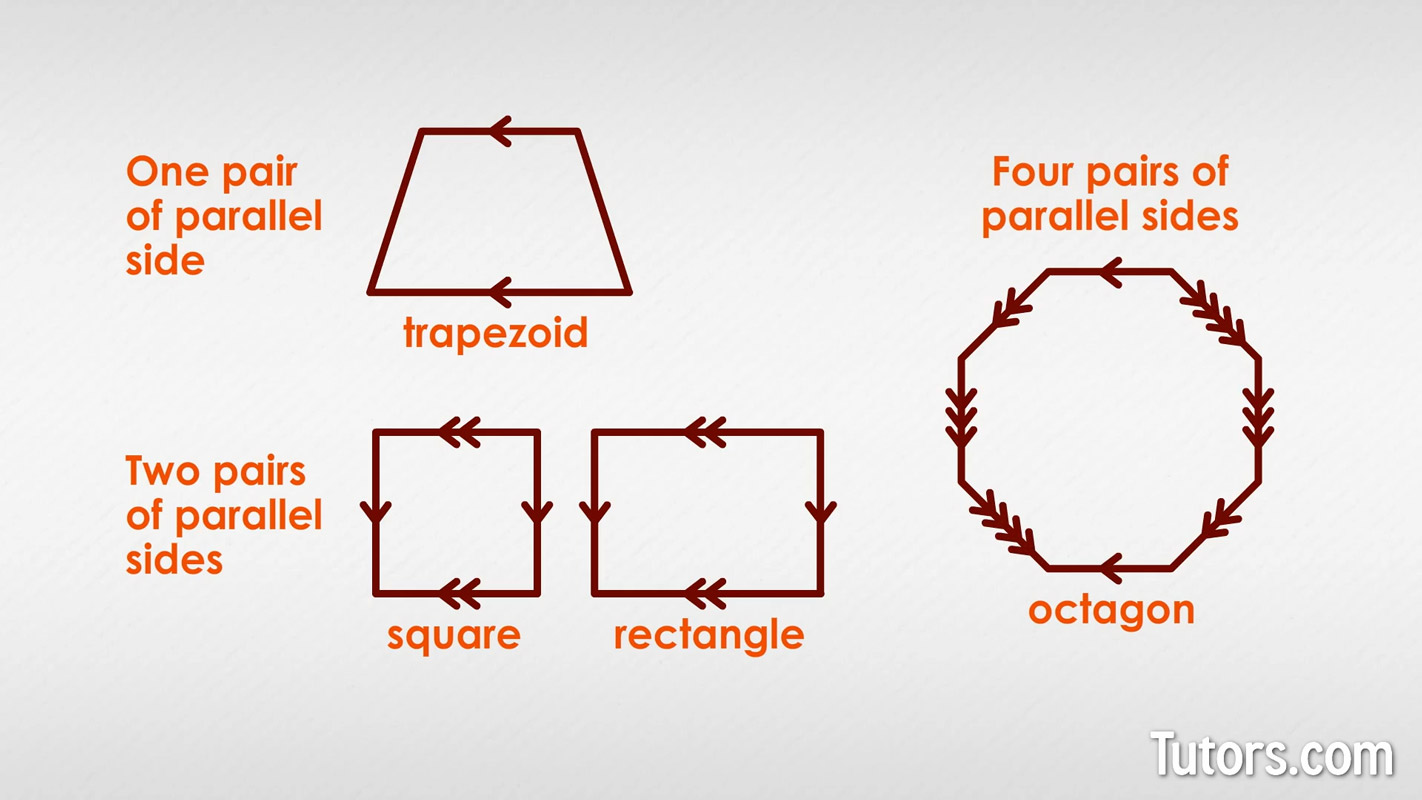
The regular polygon will have half as many pairs of parallel sides as it has sides (because two sides make a pair).

That is an interesting property of regular polygons, and of parallel sides. A regular dodecagon (12 sides) will have six pairs of parallel sides, but a regular tridecagon (13 sides) will have no parallel sides.

Parallel sides of a quadrilateral, or any polygon, must be straight sides. They can be sides of equal length, but they do not have to be.

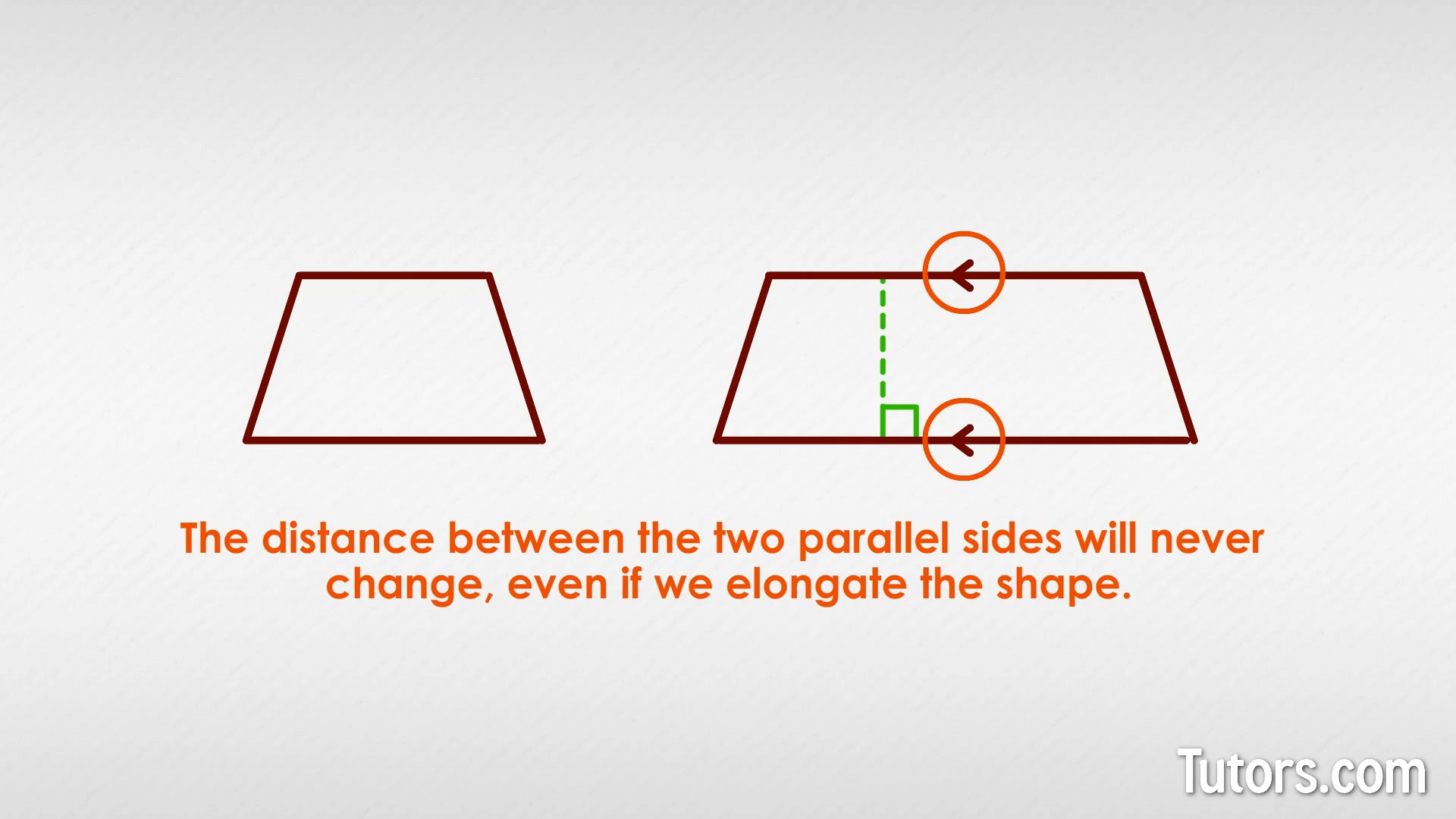
Another property of parallel sides in polygons is that the distance between the two parallel sides will never change, even if we elongate the shape:

Parallel lines symbol

You can indicate parallel sides, even if your drawing is not perfect. You can also write about parallel lines or sides using a symbol.

When drawing figures, you indicate pairs of parallel sides by drawing little matching arrowheads on the two parallel opposite sides.

If you have, say, a rectangle (with two pairs of parallel sides) you can use single arrowheads for one pair and double arrowheads for the other:

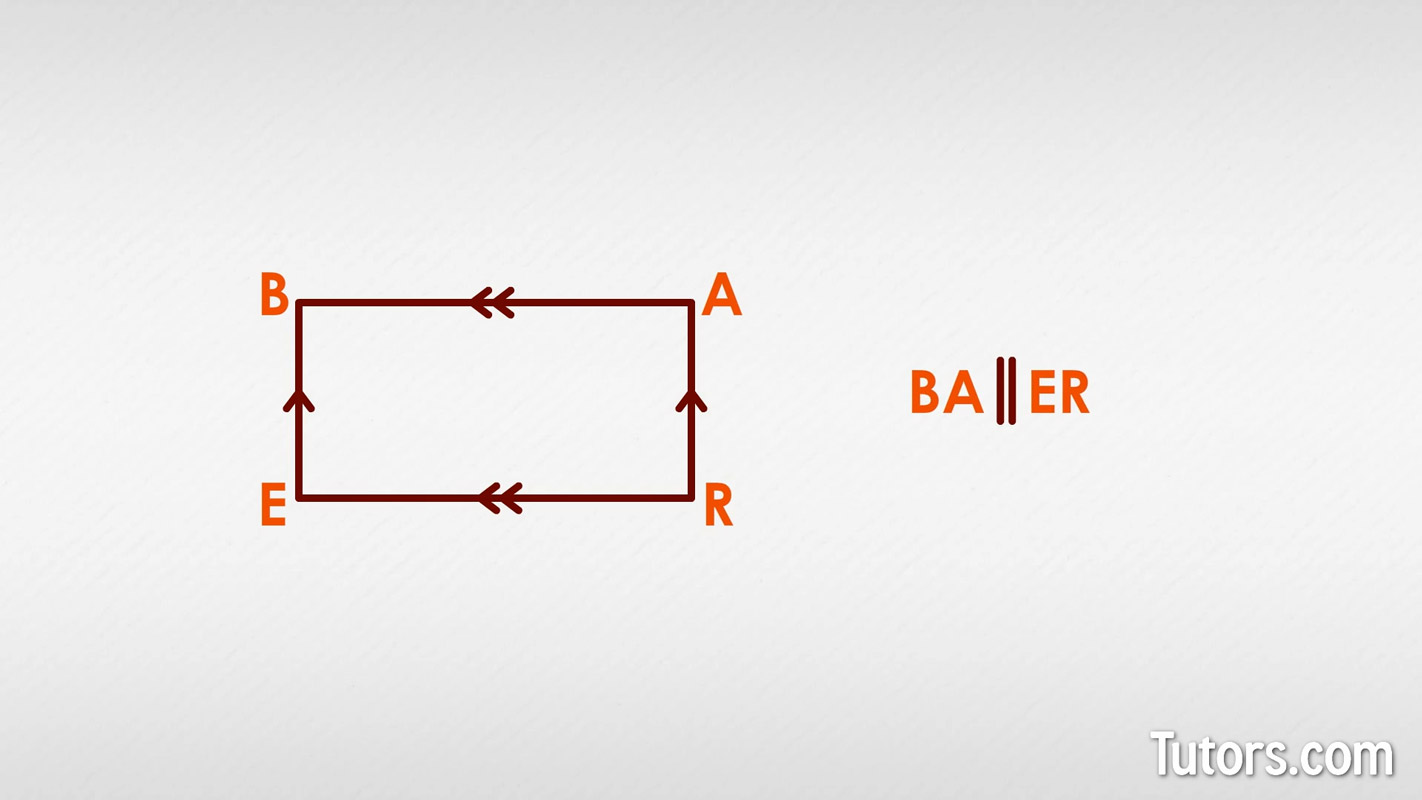
In writing about parallel sides, you can also use this symbol: ||

Many geometricians prefer this symbol because it cannot be confused for an 11 or two letter Ls. Here we are using the parallel symbol to show that line BA is parallel to line ER:

You can see that if we used to letter l's it would look like "baller," which is no help at all unless you got game.

Proving lines are parallel

In a polygon, you can test for parallel sides by checking the notation (the little arrowheads), by measuring between the two questioned lines, or by applying proofs of parallel lines from Euclid.

If you choose to measure the distance between two sides, make sure measure along a line perpendicular to the two sides, not at an angle. Measuring the angled ends of a trapezoid, for example, will not provide definite proof that the two bases (top and bottom) are parallel, because the two ends could be at different angles.

How can we prove lines are parallel? Euclid's rigor is also helpful since you can prove parallel lines using any of these methods:

1. Congruent corresponding angles

2. Congruent alternate interior angles

3. Congruent alternate exterior angles

4. Supplementary interior angles on the same side of a transversal

5. Supplementary exterior angles on the same side of a transversal