Isosceles Triangle Theorem

Isosceles Triangle Theorem (Proof, Converse, & Examples)

Isosceles triangles have equal legs (that's what the word "isosceles" means). Yippee for them, but what do we know about their base angles? How do we know those are equal, too? We reach into our geometer's toolbox and take out the Isosceles Triangle Theorem. No need to plug it in or recharge its batteries -- it's right there, in your head!

1. Isosceles Triangle
• Properties
2. Isosceles Triangle Theorem
3. Converse
4. Converse Proof

Isosceles Triangle

Here we have on display the majestic isosceles triangle, $△DUK$. You can draw one yourself, using $△DUK$ as a model.

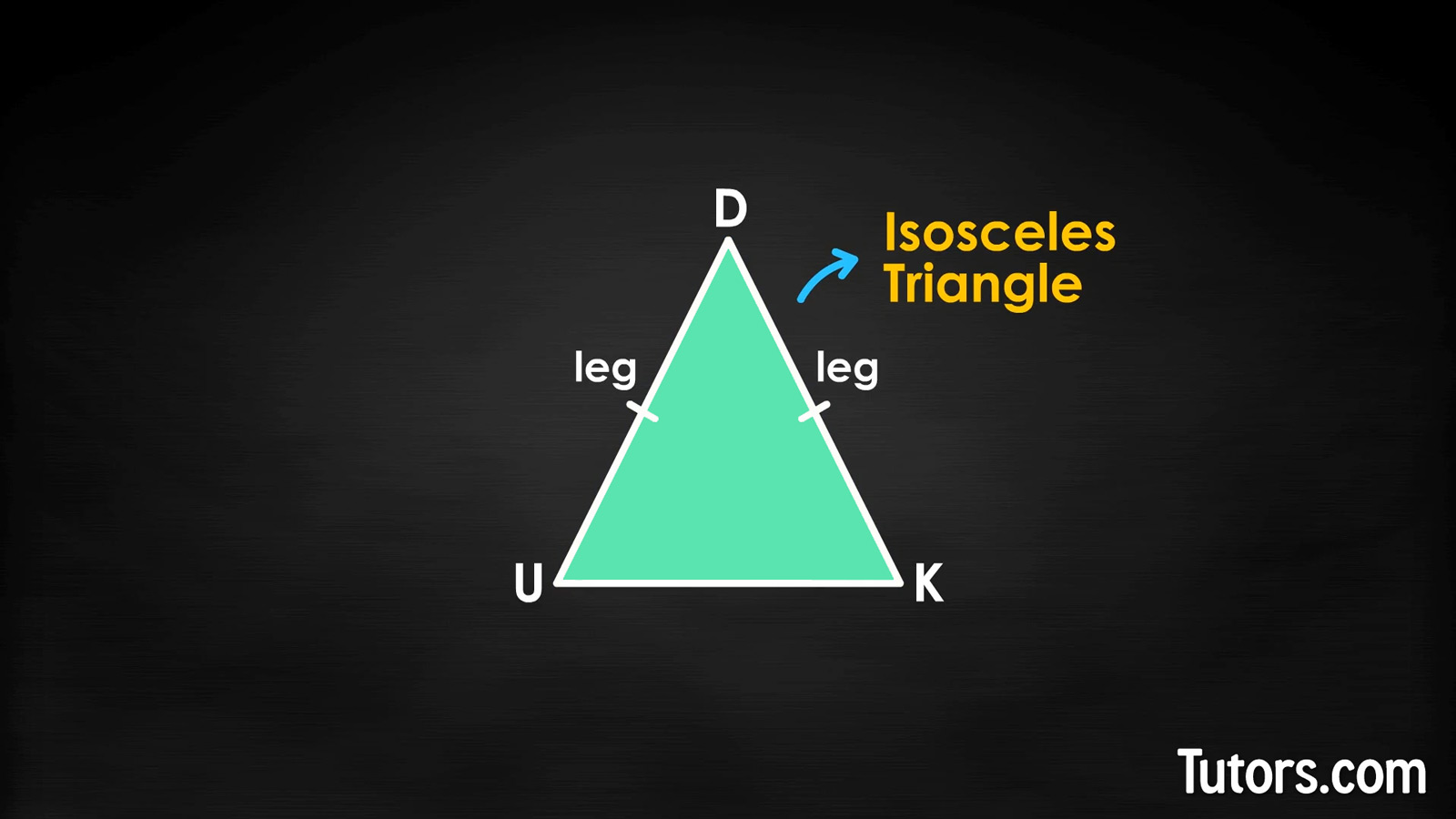
Hash marks show sides $\angle DU \cong \angle DK$, which is your tip-off that you have an isosceles triangle. If these two sides, called legs, are equal, then this is an isosceles triangle. What else have you got?

Properties of an Isosceles Triangle

Let's use $△DUK$ to explore the parts:

• Like any triangle, $△DUK$ has three interior angles: $\angle D$, $\angle U$, and $\angle K$
• All three interior angles are acute
• Like any triangle, $△DUK$ has three sides: $DU$, $UK$, and $DK$
• $\angle DU \cong \angle DK$, so we refer to those twins as legs
• The third side is called the base (even when the triangle is not sitting on that side)
• The two angles formed between base and legs, $\angle DUK$ and $\angle DKU$, or $\angle D$ and $\angle K$ for short, are called base angles:

Isosceles Triangle Theorem

Knowing the triangle's parts, here is the challenge: how do we prove that the base angles are congruent? That is the heart of the Isosceles Triangle Theorem, which is built as a conditional (if, then) statement:

To mathematically prove this, we need to introduce a median line, a line constructed from an interior angle to the midpoint of the opposite side. We find $Point C$ on base $UK$ and construct line segment $DC$:

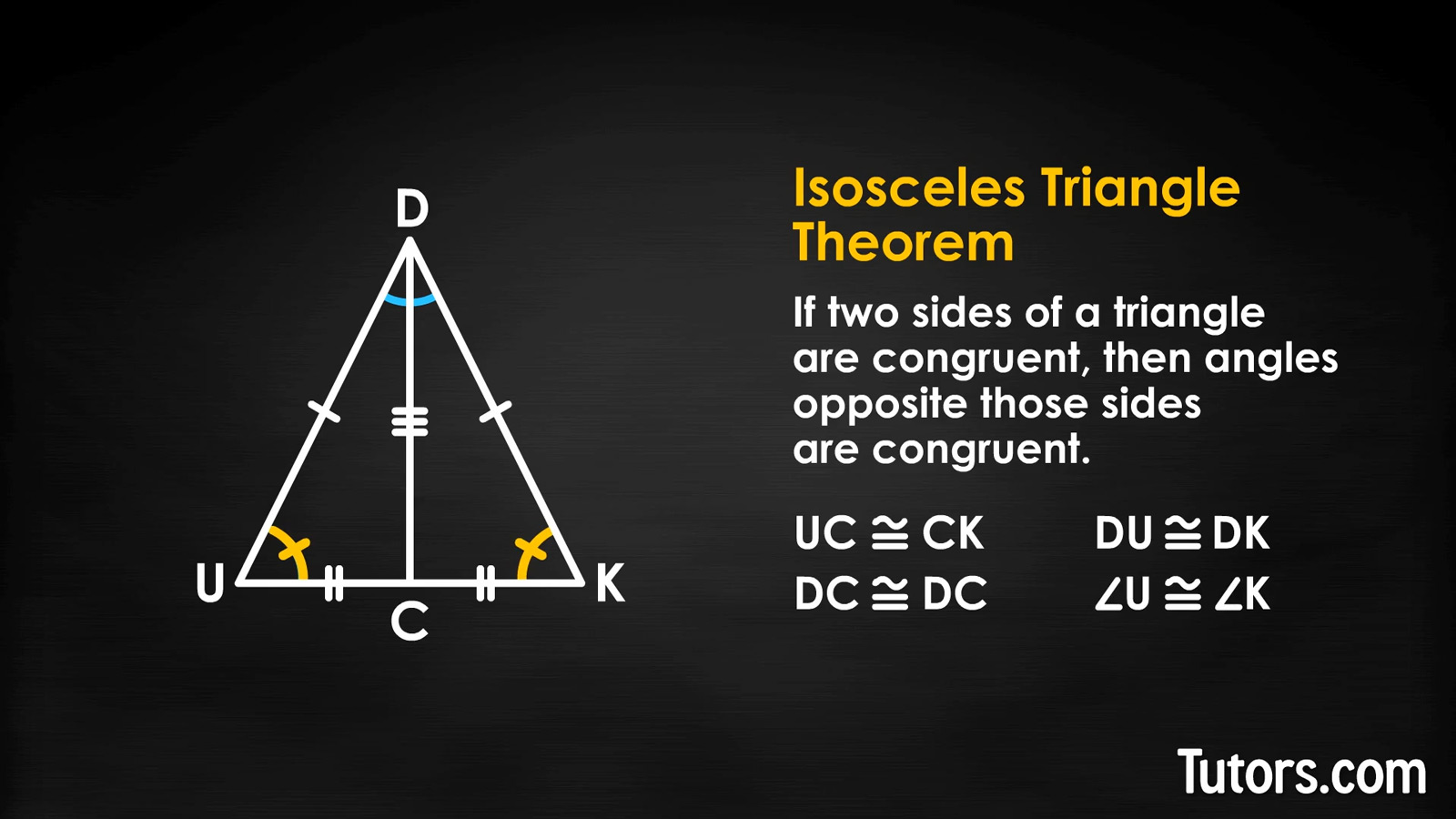
There! That's just $DUCKy$! Look at the two triangles formed by the median. We are given:

1. $UC \cong CK$ (median)
2. $DC \cong DC$ (reflexive property)
3. $DU \cong DK$ (given)

We just showed that the three sides of $△DUC$ are congruent to $△DCK$, which means you have the Side Side Side Postulate, which gives congruence. So if the two triangles are congruent, then corresponding parts of congruent triangles are congruent (CPCTC), which means …

• $\angle U \cong \angle K$

Converse of the Isosceles Triangle Theorem

The converse of a conditional statement is made by swapping the hypothesis (if …) with the conclusion (then …). You may need to tinker with it to ensure it makes sense. So here once again is the Isosceles Triangle Theorem:

If two sides of a triangle are congruent, then angles opposite those sides are congruent.

To make its converse, we could exactly swap the parts, getting a bit of a mish-mash:

If angles opposite those sides are congruent, then two sides of a triangle are congruent.

That is awkward, so tidy up the wording:

Now it makes sense, but is it true? Not every converse statement of a conditional statement is true. If the original conditional statement is false, then the converse will also be false. If the premise is true, then the converse could be true or false:

If I see a bear, then I will lie down and remain still.

If I lie down and remain still, then I will see a bear.

For that converse statement to be true, sleeping in your bed would become a bizarre experience.

Or this one:

If I have honey, then I will attract bears.

If I attract bears, then I will have honey.

Unless the bears bring honeypots to share with you, the converse is unlikely ever to happen. And bears are famously selfish.

Proving the Converse Statement

To prove the converse, let's construct another isosceles triangle, $△BER$.

Given that $\angle BER \cong \angle BRE$, we must prove that $BE \cong BR$.

Add the angle bisector from $\angle EBR$ down to base $ER$. Where the angle bisector intersects base $ER$, label it $Point A$.

Now we have two small, right triangles where once we had one big, isosceles triangle: $△BEA$ and $△BAR$. Since line segment $BA$ is an angle bisector, this makes $\angle EBA \cong \angle RBA$. Since line segment $BA$ is used in both smaller right triangles, it is congruent to itself. What do we have?

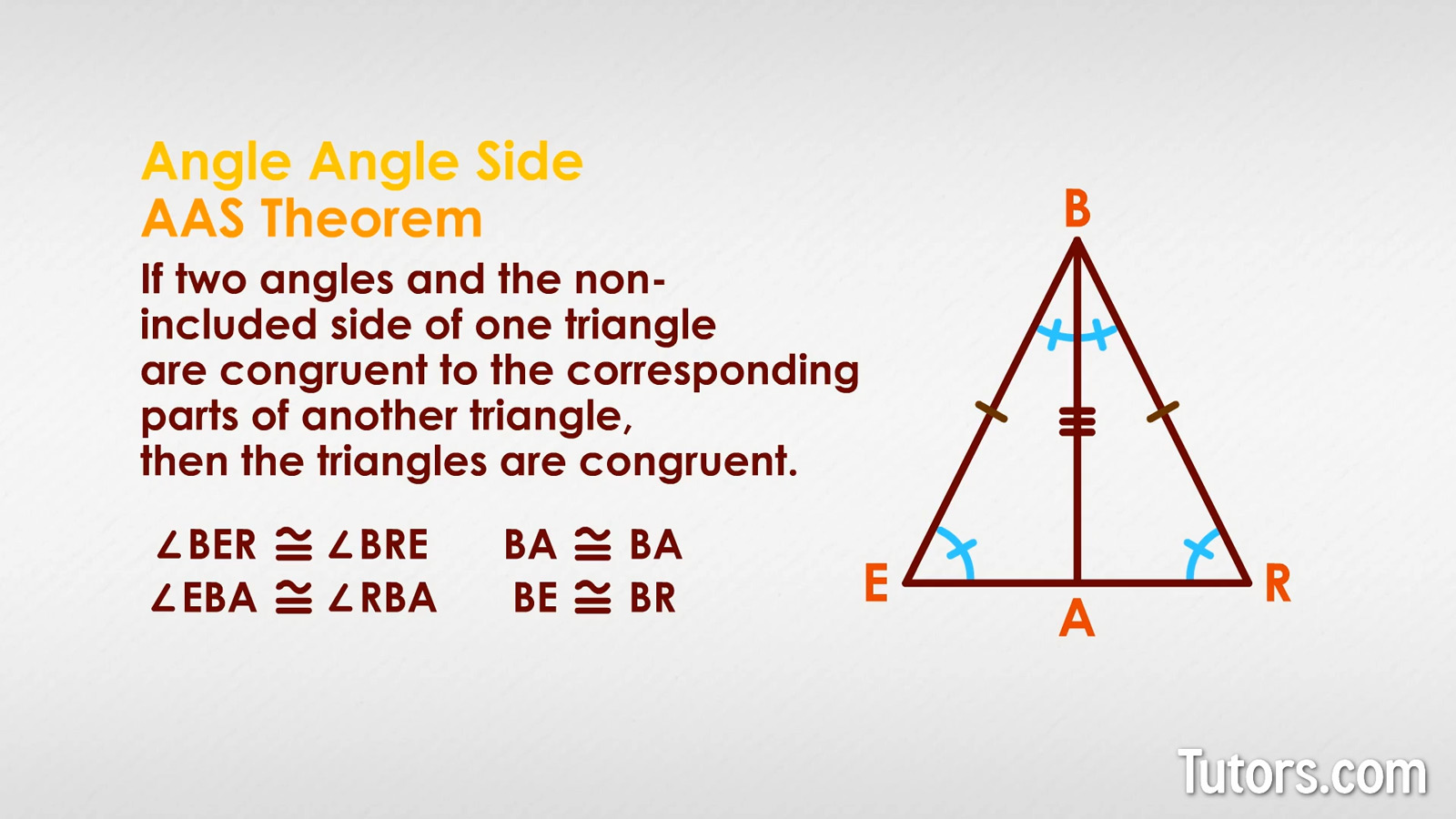
• $\angle BER \cong \angle BRE$ (given)
• $\angle EBA \cong \angle RBA$ (angle bisector)
• $BA \cong BA$ (reflexive property)

Let's see … that's an angle, another angle, and a side. That would be the Angle Angle Side Theorem, AAS:

With the triangles themselves proved congruent, their corresponding parts are congruent (CPCTC), which makes $BE \cong BR$. The converse of the Isosceles Triangle Theorem is true!

Lesson Summary

By working through these exercises, you now are able to recognize and draw an isosceles triangle, mathematically prove congruent isosceles triangles using the Isosceles Triangles Theorem, and mathematically prove the converse of the Isosceles Triangles Theorem. You also should now see the connection between the Isosceles Triangle Theorem to the Side Side Side Postulate and the Angle Angle Side Theorem.

Next Lesson:

Alternate Exterior Angles