Interior Angle Formula
Interior angle formula (definition, examples, sum of Interior angles)
If you take a look at other geometry lessons on this helpful site, you will see that we have been careful to mention interior angles, not just angles, when discussing polygons. Every polygon has interior angles and exterior angles, but the interior angles are where all the interesting action is.
Interior angle formula
From the simplest polygon, a triangle, to the infinitely complex polygon with n sides, sides of polygons close in a space. Every intersection of sides creates a vertex, and that vertex has an interior and exterior angle. Interior angles of polygons are within the polygon.
Though Euclid did offer an exterior angles theorem specific to triangles, no Interior Angle Theorem exists. Instead, you can use a formula that mathematically describes an interesting pattern about polygons and their interior angles.
Sum of interior angles formula
This formula allows you to mathematically divide any polygon into its minimum number of triangles. Since every triangle has interior angles measuring 180°, multiplying the number of dividing triangles times 180° gives you the sum of the interior angles.
S = sum of interior angles
n = number of sides of the polygon
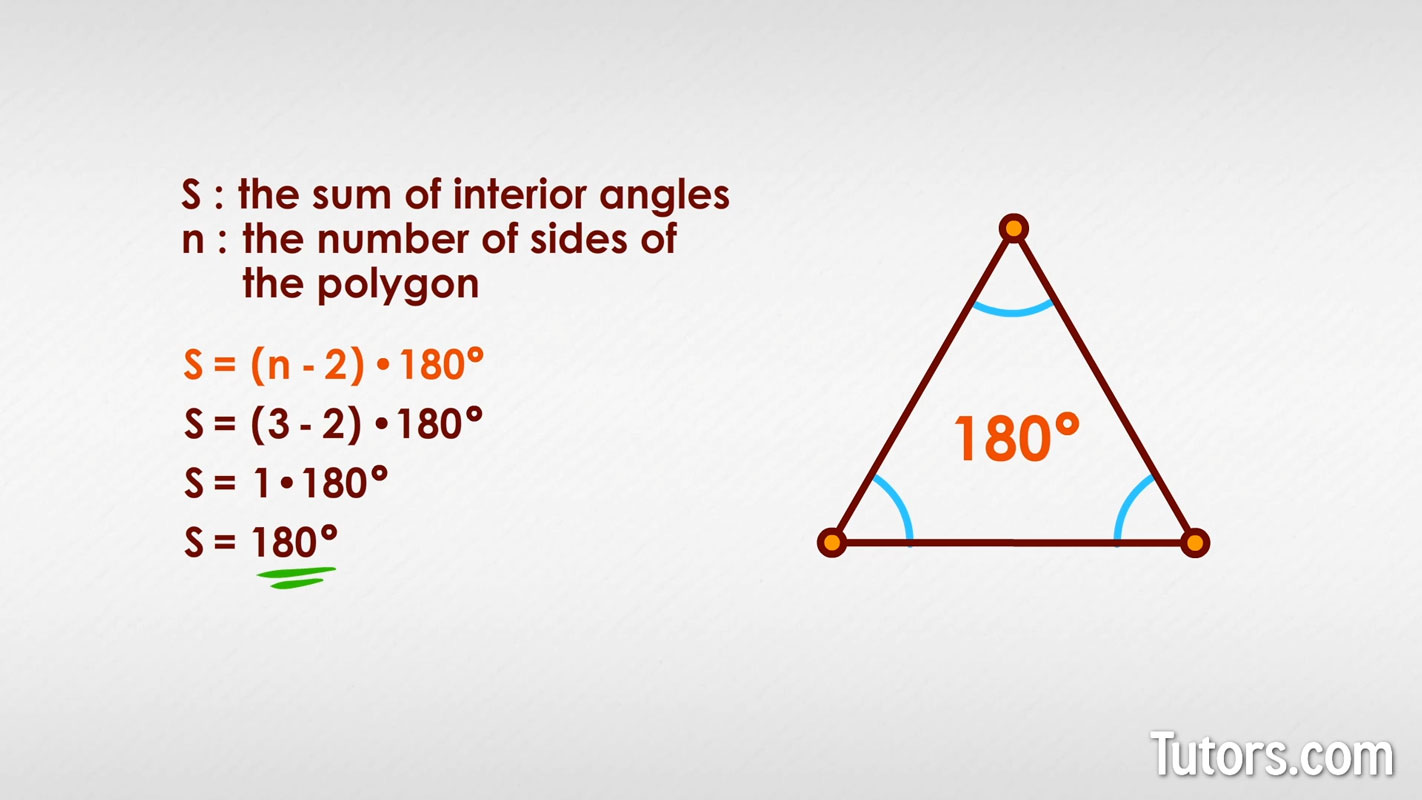
Try the formula on a triangle:
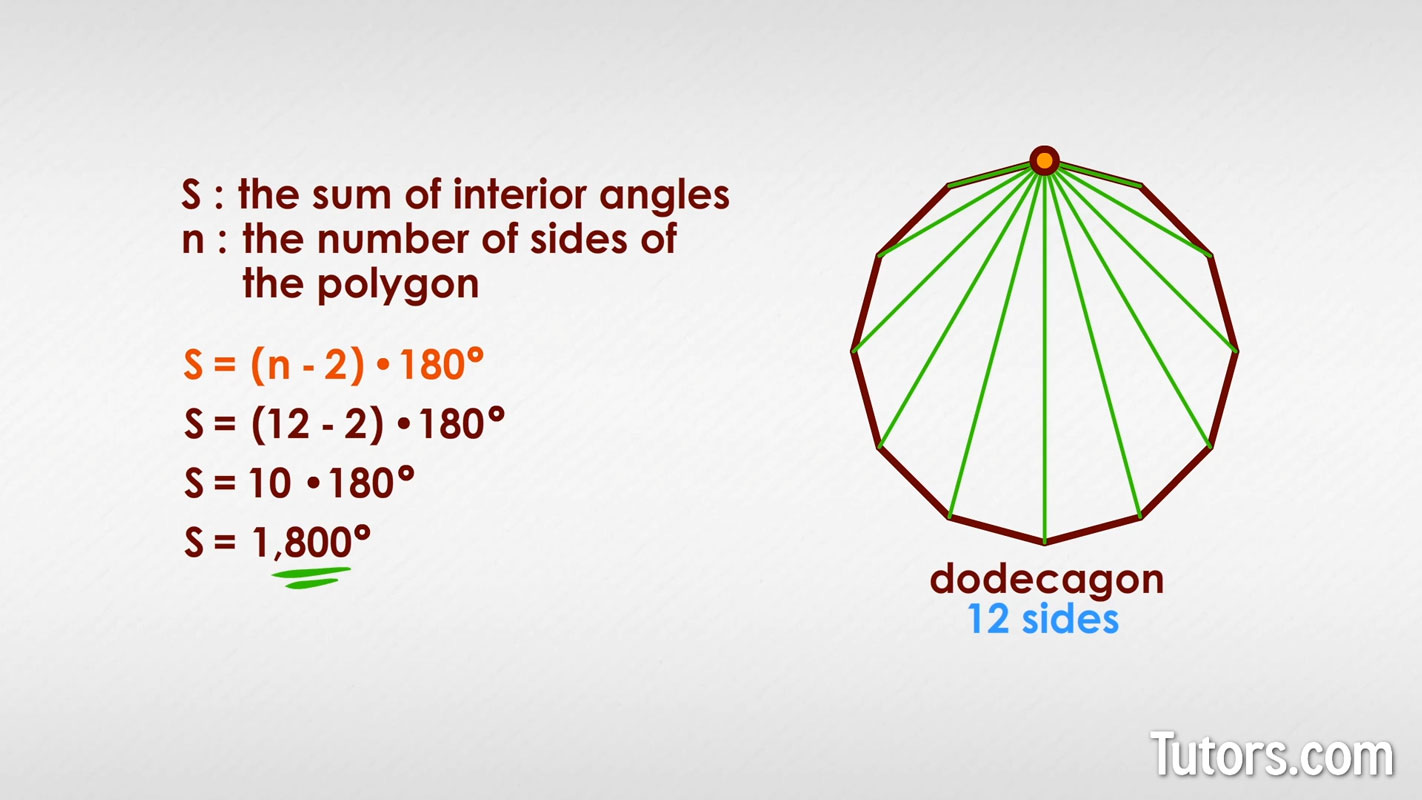
Well, that worked, but what about a more complicated shape, like a dodecagon? It has 12 sides, so:
How do you know that is correct?
Take any dodecagon and pick one vertex. Connect every other vertex to that one with a straightedge, dividing the space into 10 triangles. Ten triangles, each 180°, makes a total of 1,800°!
Finding an unknown interior angle
The same formula can help you find a missing interior angle of a polygon. Here is a wacky pentagon, with no two sides equal:
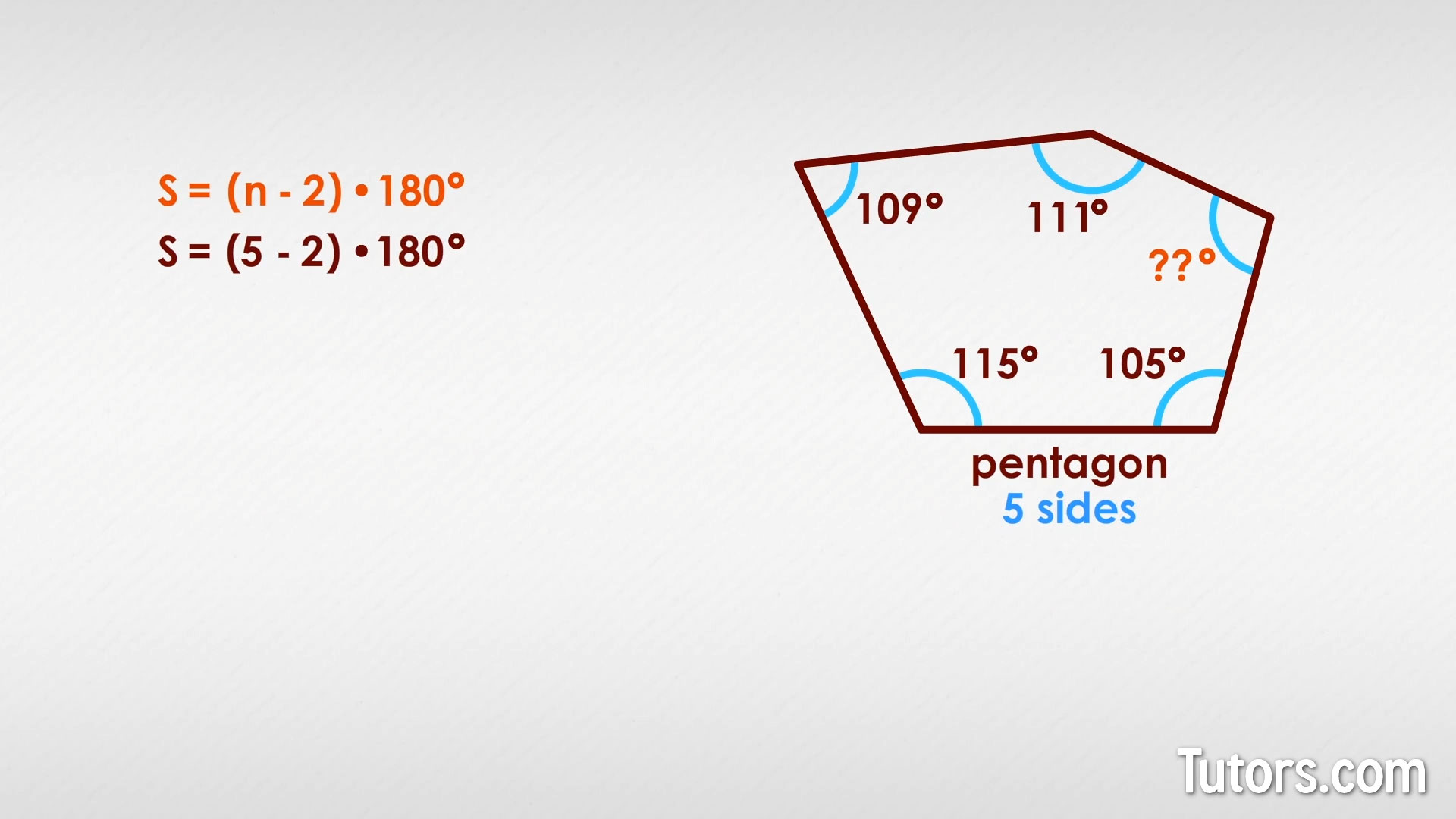
The formula tells us that a pentagon, no matter its shape, must have interior angles adding to 540°:
So subtracting the four known angles from 540° will leave you with the missing angle:
The unknown angle is 100°.
Finding interior angles of regular polygons
Once you know how to find the sum of interior angles of a polygon, finding one interior angle for any regular polygon is just a matter of dividing.
Where S=the sum of the interior angles and n=the number of congruent sides of a regular polygon, the formula is:
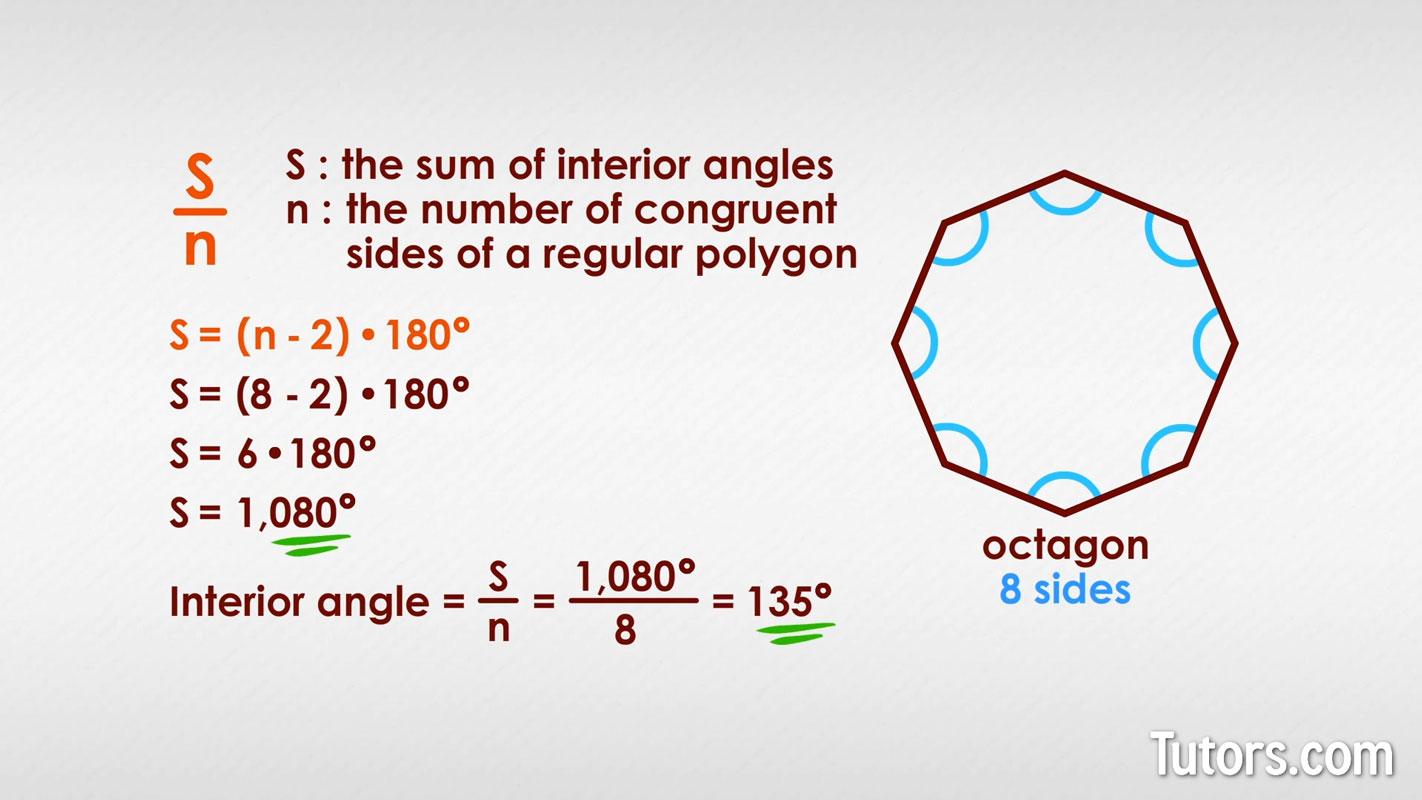
Here is an octagon (eight sides, eight interior angles). First, use the formula for finding the sum of interior angles:
Next, divide that sum by the number of sides:
measure of each interior angle =
measure of each interior angle =
measure of each interior angle =
Each interior angle of a regular octagon is = 135°.
Finding the number of sides of a polygon
You can use the same formula, S=(n-2)×180°, to find out how many sides n a polygon has, if you know the value of S, the sum of interior angles.
You know the sum of interior angles is 900°, but you have no idea what the shape is. Use what you know in the formula to find what you do not know:
State the formula:
Use what you know, S=900°:
Divide both sides by 180°:
No need for parentheses now:
Add 2 to both sides:
The unknown shape was a heptagon!
Lesson summary
Now you are able to identify interior angles of polygons, and you can recall and apply the formula, S=(n−2)×180°, to find the sum of the interior angles of a polygon. You also are able to recall a method for finding an unknown interior angle of a polygon, by subtracting the known interior angles from the calculated sum.
Not only all that, but you can also calculate interior angles of polygons using , and you can discover the number of sides of a polygon if you know the sum of their interior angles. That is a whole lot of knowledge built up from one formula, S=(n−2)×180°.