Inscribed Angle — Definition, Theorem & Formula
Parts of a circle
A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line.
A circle has parts:
Arc - a portion of the circle's circumference
Center - the direction center point inside the circle
Chord - a line connecting two points on the circle
Circumference - the distance around the circle
Diameter - a chord through the circle's center
Radius - half the diameter
A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. Circles are almost always indicated by the mathematical symbol followed by the circle's letter designation, its center point. This, for example, is A with chord BC and arc DE:
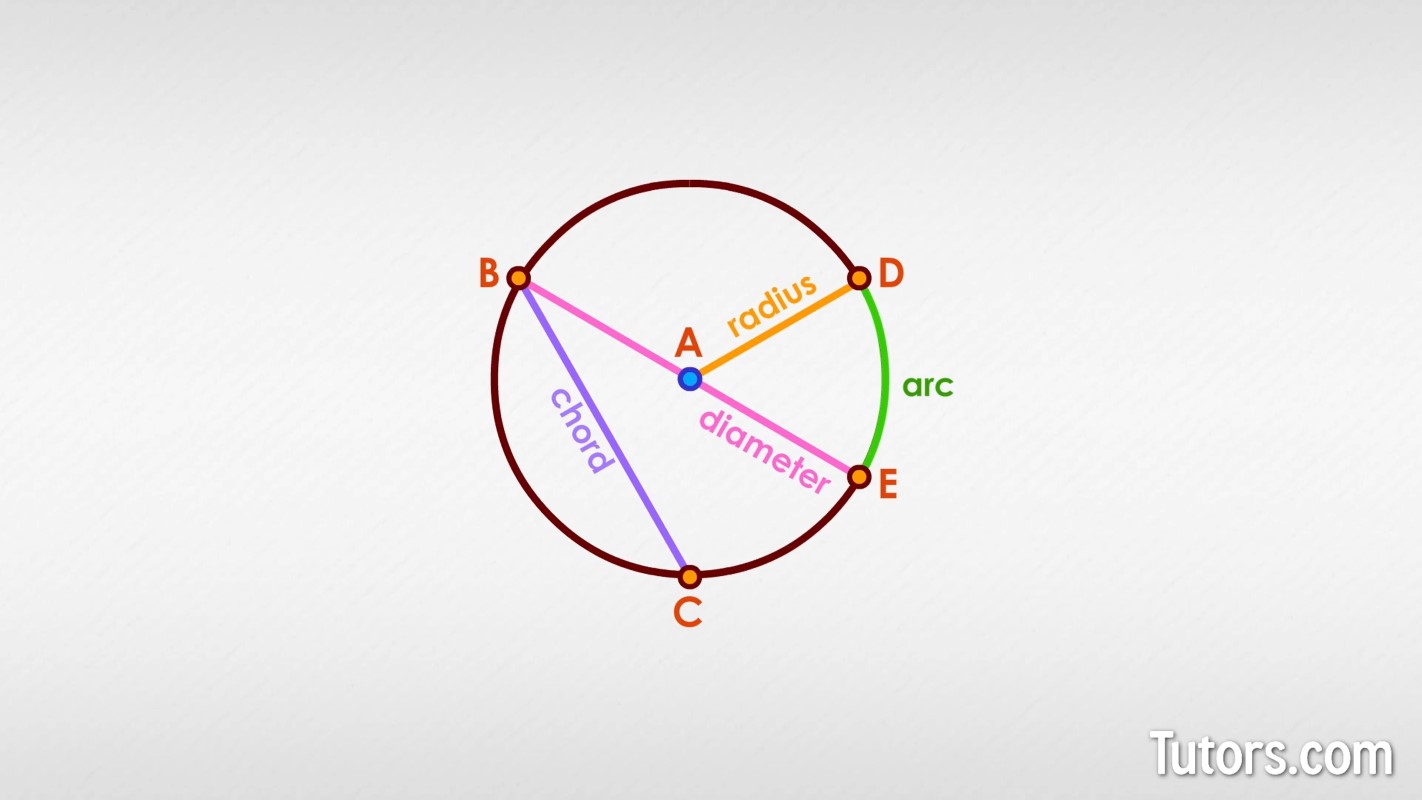
If you constructed a line segment from Point A (the circle's center) to Point D on the circle, that line segment would be a radius. Running a chord from Point B to Point E would give you a diameter, which must run through the center of the circle.
With circles, geometry becomes at once more interesting and more difficult. Combining curves and straight lines, circles create whole new possibilities. A common figure involving a circle is an inscribed angle.
Inscribed angle definition
An inscribed angle is an angle whose vertex lies on a circle and its two sides are chords of the same circle. In the circle below, we have constructed an inscribed angle:
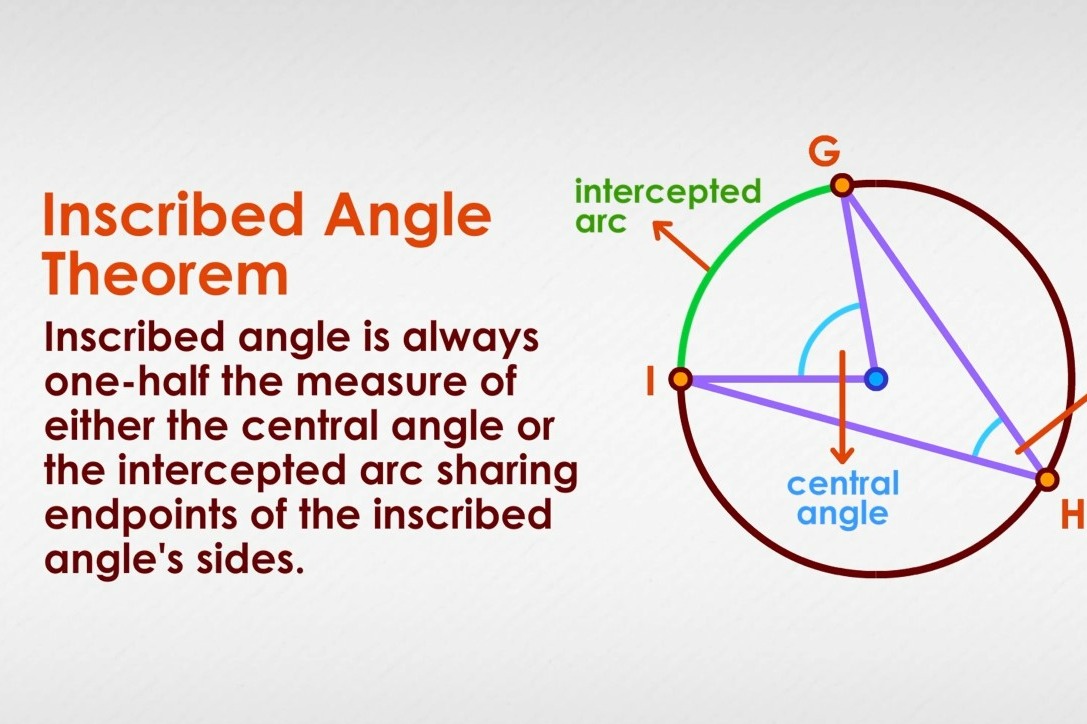
We selected three points on the circle, Points G, H, and I
We connected G and H with a chord, GH
We connected H to I with a chord, HI
is the inscribed angle
Inscribed angle theorem
The Inscribed Angle Theorem tells us that an inscribed angle is always one-half the measure of either the central angle or the intercepted arc sharing endpoints of the inscribed angle's sides.
Let's take a look at our formula:
For example, let's take our intercepted arc measure of 80°. If the inscribed angle is half of its intercepted arc, half of 80 equals 40. So, the inscribed angle equals 40°.
Another way to state the same thing is that any central angle or intercepted arc is twice the measure of a corresponding inscribed angle.
Both ways equal 40°!
What is a central angle?
A central angle of a circle is an angle that has its vertex at the circle's center point and its two sides are radii. The central angle creates an arc between the two endpoints of the angle's sides, on the circle.
What is an intercepted arc?
An intercepted arc is the portion of a circle's circumference limited by the sides of an inscribed angle. In our drawing above, the part of the circle from Point G to Point I is the intercepted arc. This is conveniently indicated with the symbol of a small arc over the letters:
Inscribed angle relationships
Circles have some surprising relationships between their parts. For any inscribed angle, the measure of the inscribed angle is one-half the measure of the intercepted arc. That, of course, is the Inscribed Angle Theorem.
An inscribed angle has very few rules. Its vertex and endpoints of its sides must lie on the circle, and that's about it. That means an intercepted arc can have dozens -- even hundreds -- even thousands! -- of inscribed angles. You can move the vertex of the inscribed angle around the circle, keeping the sides' endpoints pinned to the intercepted arc.
Here, look. All these inscribed angles are for the same intercepted arc:
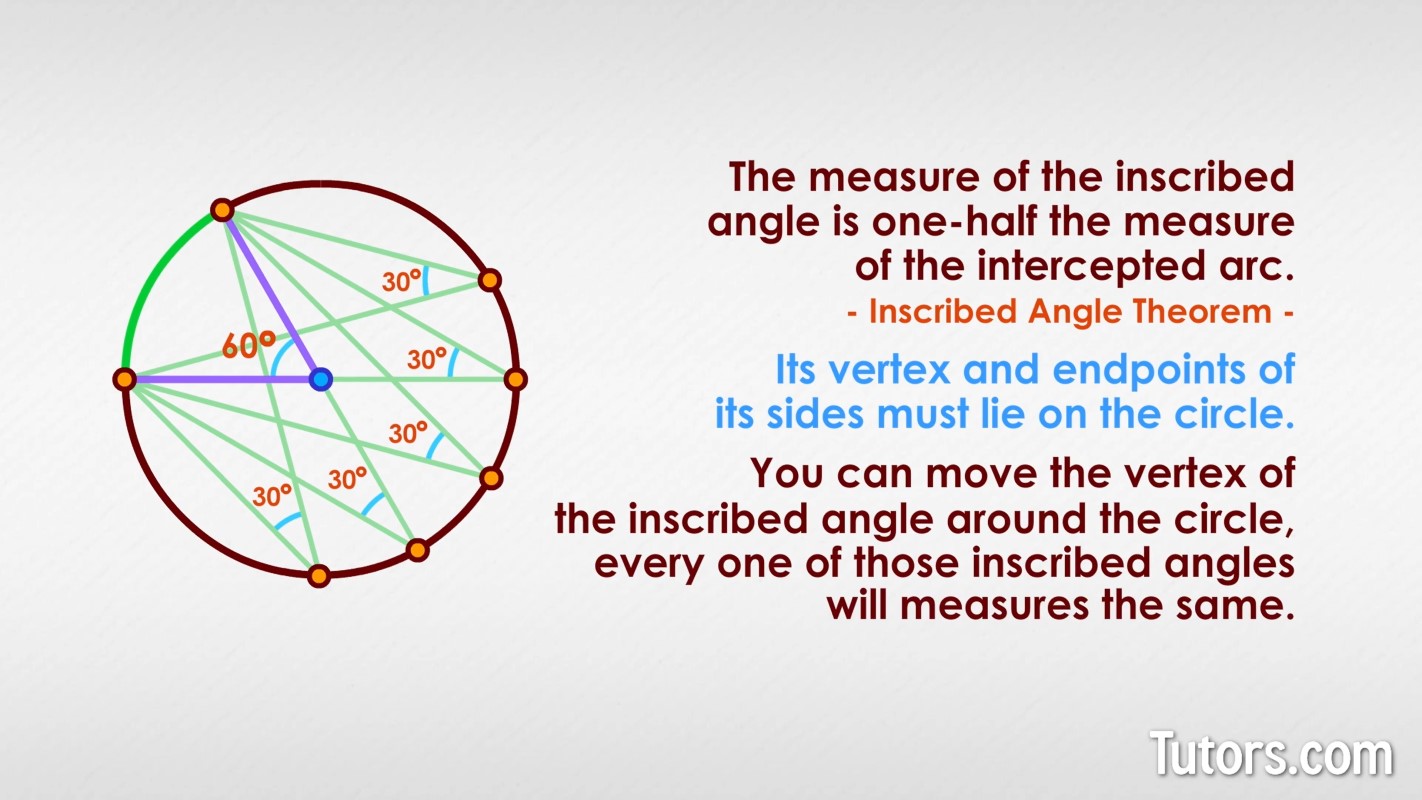
And yet, every one of those inscribed angles measures 30°, in compliance with the Inscribed Angle Theorem!
Lesson summary
Now that you have studied this lesson, you are able to identify an inscribed angle and a central angle of a circle, identify and name the circle's intercepted arc created by the inscribed angle, and recall, state and apply the Inscribed Angle Theorem, which says the measure of a given intercepted arc is twice the measure of an inscribed angle to that intercepted arc.