Decagon — Sides, Shapes, Angles, & Definition
Decagons definition
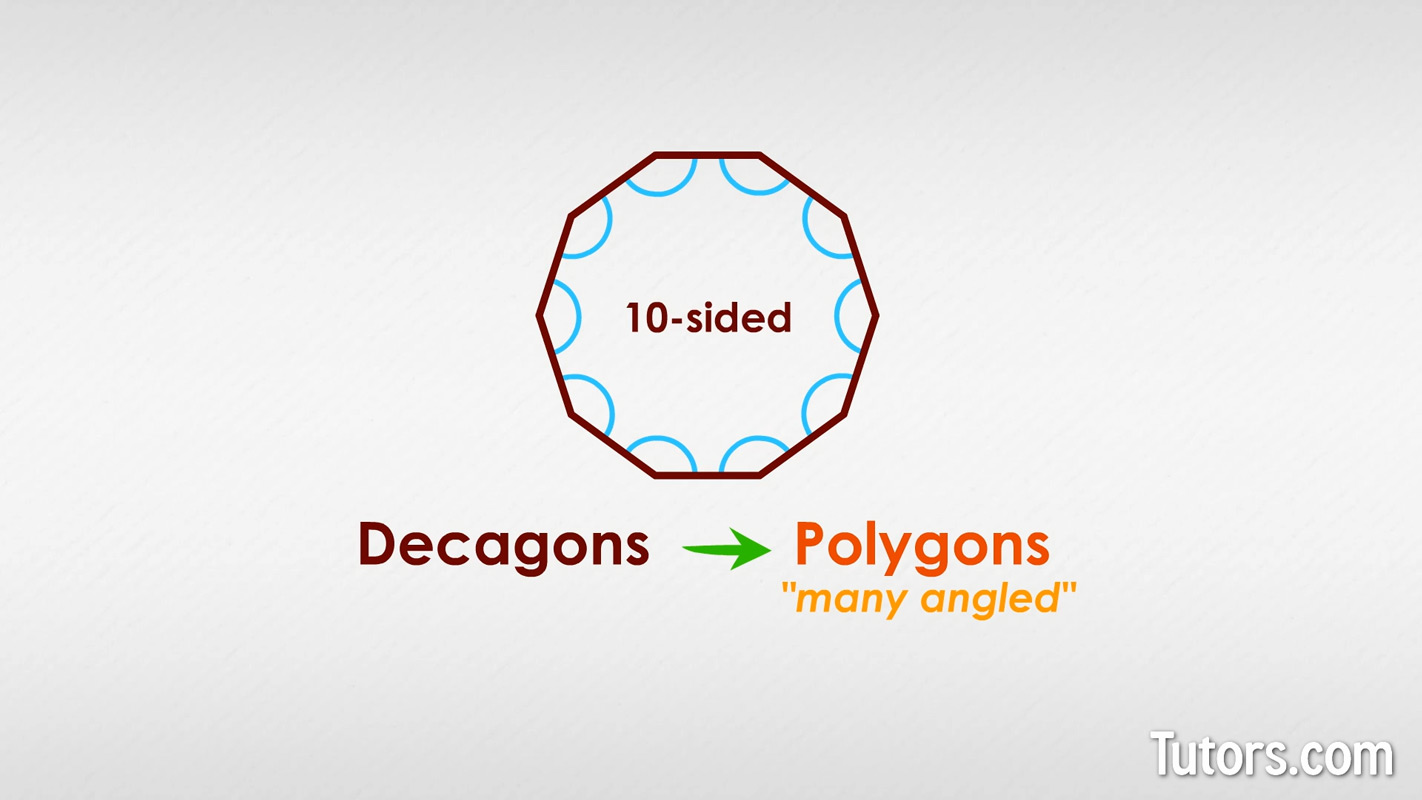
A decagon is a 10-sided polygon, with 10 interior angles, and 10 vertices which is where the sides meet.
Polygons get their name from Greek, meaning "many-angled," because all polygons have multiple interior angles. They close in a two-dimensional space using only straight sides.
Properties of decagons
For a polygon to be a decagon, it must have these identifying properties:
10 sides
10 interior angles
10 vertices
Decagon angles
In many decagons, the sum of interior angles will be 1,440°, but that is not an identifying property because complex decagons will not have that sum.
Regular decagons have two additional identifying properties:
10 exterior angles of 36°, summing to 360°
10 interior angles of 144°, summing to 1,440°

Drawing a decagon takes no skill; simply draw 10 line segments that connect, and you have it. Drawing a regular, convex decagon, however, takes real skill, since each interior angle must be 144°, and all sides must be equal in length.
Drawing a concave decagon is actually fairly easy: make a five-pointed star and fill it in. That is the star that appears 50 times on the Unites States flag, and the outline of such a pentagram (five-pointed star) is a decagon.
Types of decagons
A decagon is a 10-sided polygon, with 10 interior angles, and 10 vertices which is where the sides meet.
A regular decagon has 10 equal-length sides and equal-measure interior angles. Each angle measures 144° and they all add up to 1,440°.
An irregular decagon has sides and angles that are not all equal or congruent.
A convex decagon bulges outward, with no interior angle greater than 180°.
A concave decagon have indentations, creating interior angles greater than 180°.
A simple decagon does not have any sides that cross or intersect.
A complex decagon has self-intersecting sides, is complex, and highly irregular.

Regular and irregular decagons
All polygons can be drawn as regular (equal-length sides, equal-measure interior angles) or irregular (not restricted to congruent angles or sides). The regular, convex decagon is a subtle and elegant shape, with 10 exterior angles of 36°, 10 interior angles of 144°, and 10 vertices (intersections of sides).

Because it is a challenging shape to make, the regular, convex decagon is popular with coins (like those from Australia, Belize and Hong Kong). Irregular decagons must simply have 10 sides closing in a space, but the lengths of their sides can vary greatly.
Concave and convex decagons
Most polygons can be convex or concave. Convex decagons bulge outward, with no interior angle greater than 180°. Concave decagons have indentations, creating interior angles greater than 180°. That is why the outline of a five-pointed star is a concave decagon; it has five interior angles each of which is far greater than 180°.

So far all the decagons discussed - regular, irregular, concave, and convex - share the same properties:
10 sides
10 vertices
10 interior angles
Simple and complex decagons
Decagons can be simple or complex. A simple decagon has no sides crossing themselves. A simple decagon follows all the conventional "rules" of polygons.
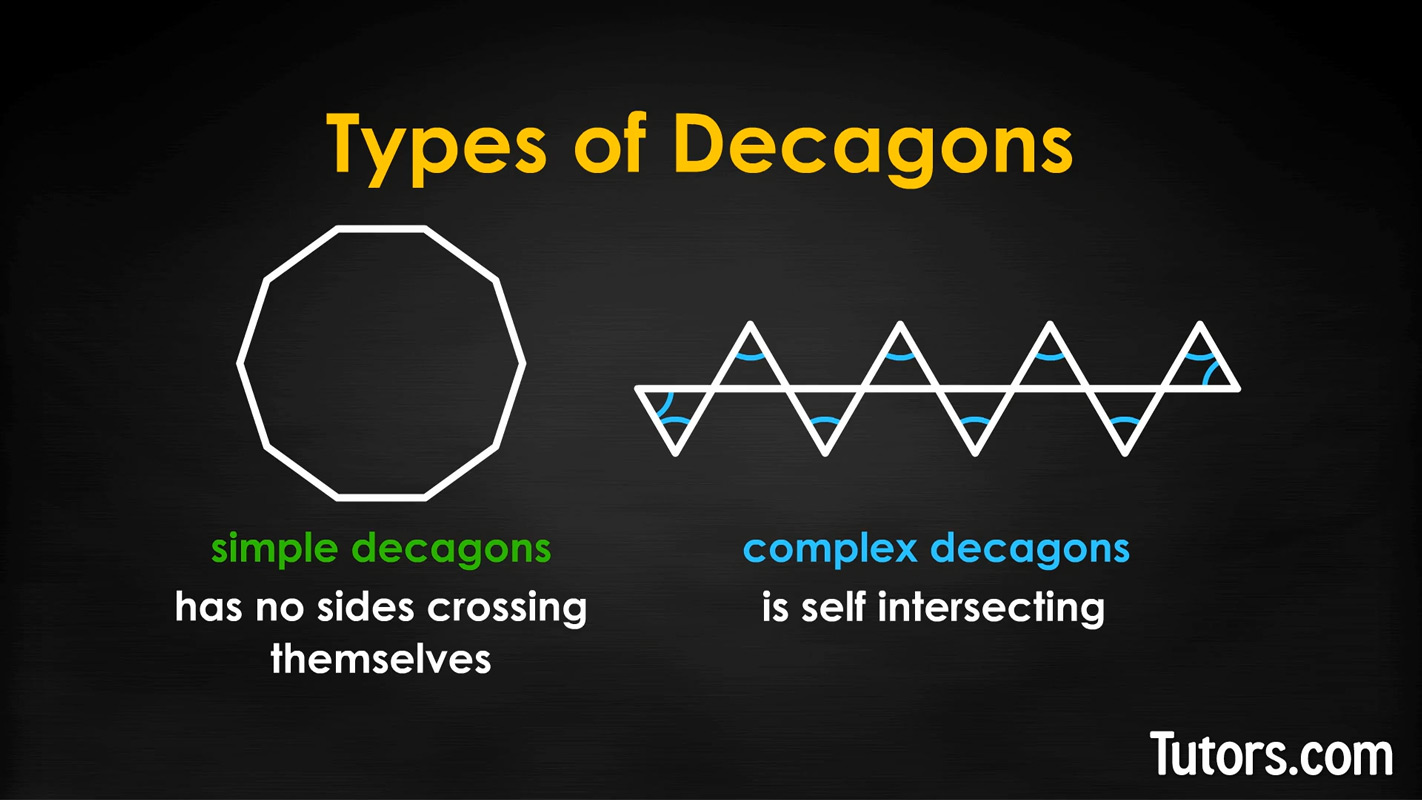
By contrast, a complex decagon is self-intersecting. In crossing its own sides, a complex decagon sets off additional interior spaces, but it is still said to have only 10 sides, 10 interior angles, and 10 vertices. Because it is so highly irregular and self-intersecting, a complex decagon need not follow any predictable rule about interior angles or their sums.
Notice that a single decagon can fit into several categories. The classic regular decagon meets all these requirements:
Regular decagon
Convex decagon
Simple decagon