Angle Bisector Theorem & Definition

Written by

Malcolm McKinsey

January 20, 2023

Fact-checked by

Paul Mazzola

Angle bisector definition

The Angle Bisector Theorem helps you find unknown lengths of sides of triangles, because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangle's other two sides.

How to construct an angle bisector

Draw △ABC on a piece of paper. Interior angles A, B, C have opposite sides a, b, c.

Get some linear object and put one endpoint at ∠A. Allow its other end to cross side aa. Divide ∠A into two equal angles. You bisected ∠A.

The linear object is an angle bisector. When it crossed side aa opposite ∠A, it divided △ABC into two smaller triangles and divided side aa in two.

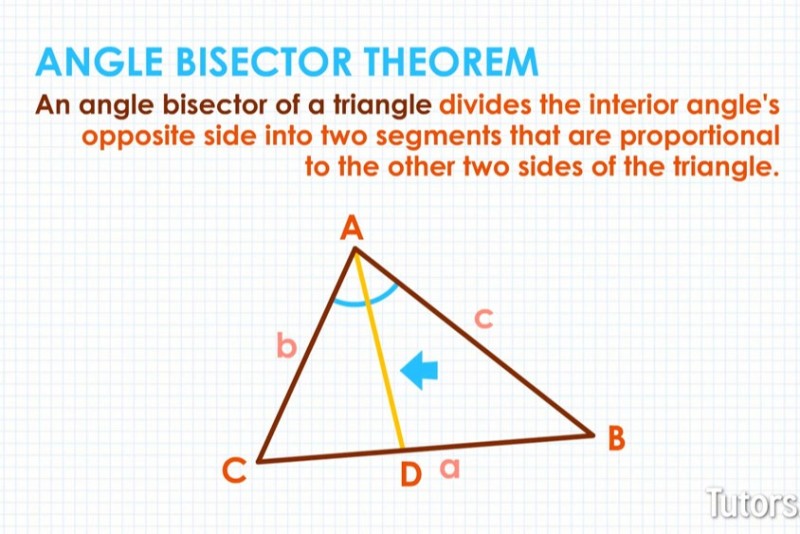
Replace your object with a drawn line segment or ray. Where the angle bisector crosses side aa, label that point D. The angle bisector is now line segment AD and creates two smaller triangles, △ACD and △ABD. Side aa is now two line segments, CD and DB.

Angle bisector theorem

One version of the Angle Bisector Theorem is an angle bisector of a triangle divides the interior angle's opposite side into two segments that are proportional to the other two sides of the triangle.

Angle bisector AD cuts side aa into two line segments, CD and DB. CD and DB relate to sides b (CA) and c (BA) in the same proportion as CA and BA relate to each other. △ACD and △ABD, created by the angle bisector, are also similarly proportional.

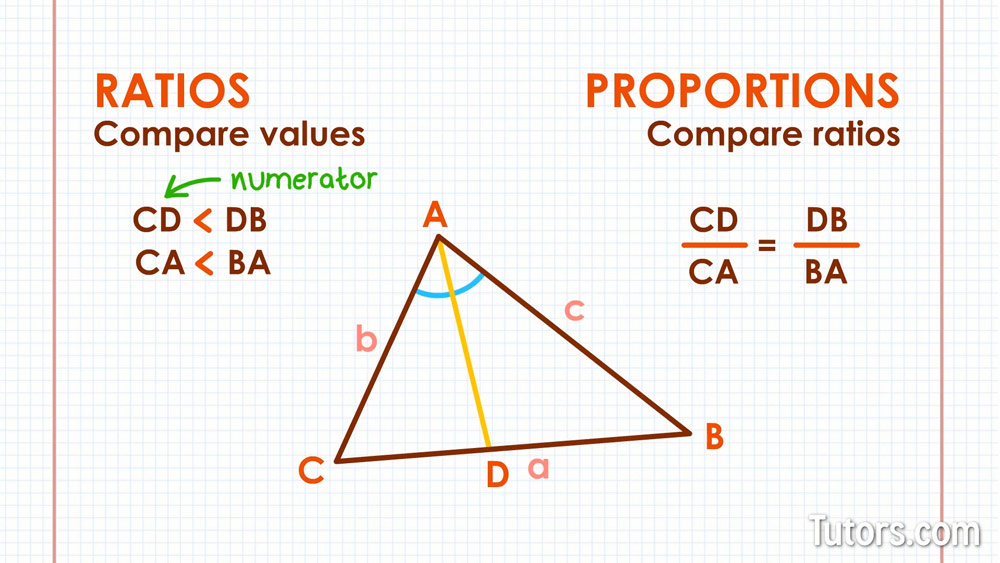
Ratios & proportions

Ratios compare values. You can establish ratios between sides CA and BA, and line segments CD and DB. Proportions compare ratios; you can learn if two ratios are equal.

For △ABC with angle bisector AD, sides CA and BA, and side aa divided into CD and DB, we can set up ratios between the sides and line segments and compare them:

Line segment CD (from angle bisector AD) has the same ratio to line segment DB as the triangle's side CA has to side BA.

Be careful to set up the ratios correctly. CD is the smaller of the two line segments, so it is the numerator of our ratio. DB is the longer line segment. So CD is to DB as the triangle's shorter side CA, is to the triangle's longer side BA.

Other ratios emerge, too. Compare line segments of the side divided by the angle bisector to the remaining sides:

The relationship of the two sides of the new, smaller △CDA is the same relationship as the two sides of new, smaller △DBA. They are in the same proportions.

Angle bisector examples

Suppose we are told a line segment AD divides side a into CD and DB, of lengths 10 cm and 30 cm. We are also told side CA is 30 cm and side BA is 90 cm. See if the ratios are proportional to each other:

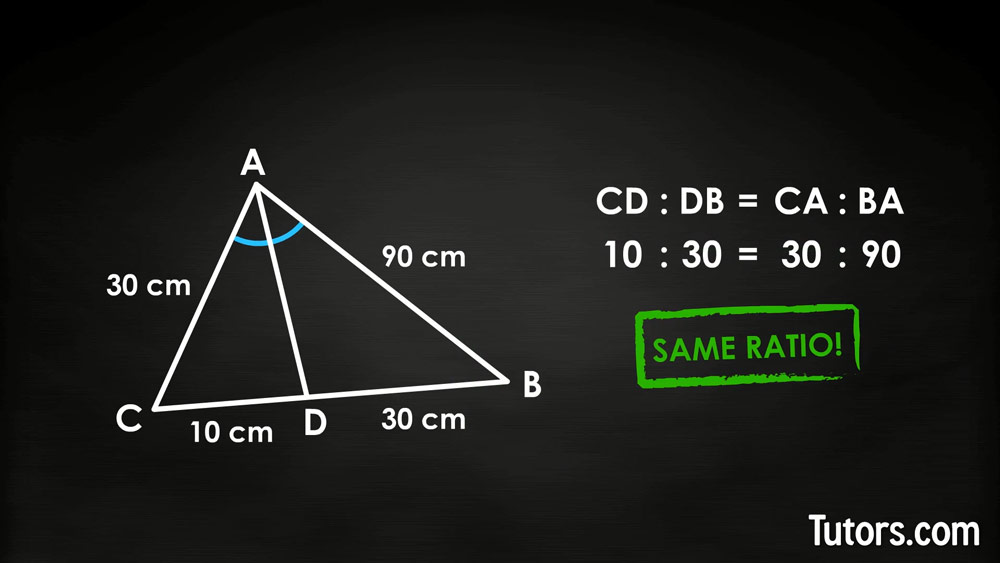
We see $\frac{10}{30}$ is the same ratio as $\frac{30}{90}$, so AD is an angle bisector.

Angle bisector of a triangle

Using the angle bisector theorem to find an unknown side

If we know the length of original sides a and b, we can use the Angle Bisector Theorem to find the unknown length of side c. The angle bisector divides side a into CD and DB (the total length of side a, CB).

Assume these lengths:

Recall our ratios and substitute the values:

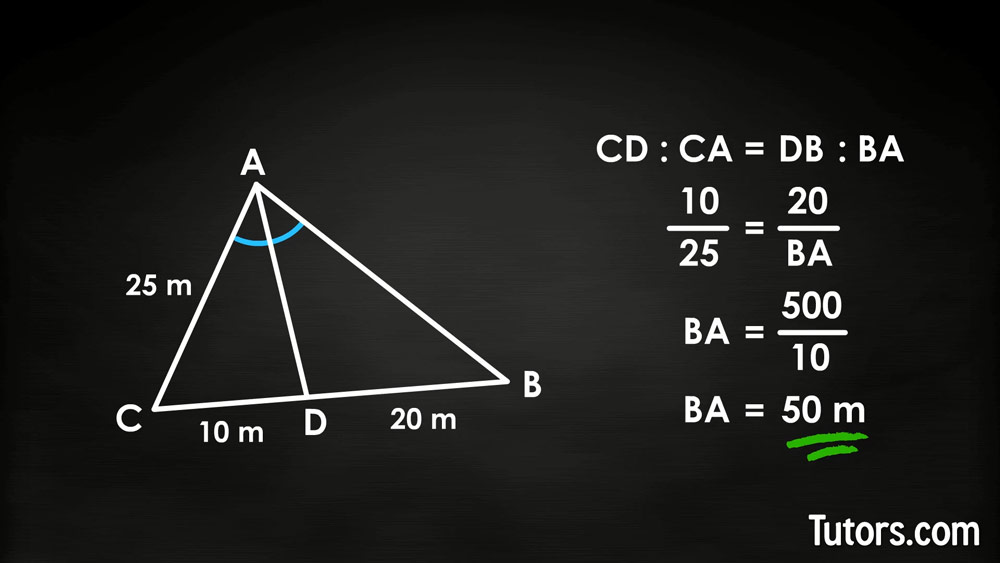
Using cross multiplication ($25\times 20=500$) and then division ($\frac{500}{10}$) , we get $BA=50 meters$.

Lesson summary

You are now able to define the Angle Bisector Theorem, use ratios and proportions to verify an angle is a bisector, use the Angle Bisector Theorem to find the unknown lengths of sides of triangles, and identify an angle bisector by evaluating the lengths of the sides of the triangle.