Irregular Quadrilaterals — Definition & Area

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Quadrilateral definition

To recall, a quadrilateral (Latin: "four sides") is a two-dimensional plane figure that uses four line segments to enclose a space. Because the definition is so broad, many common shapes are quadrilaterals:

1. Squares

2. Rectangles

3. Trapezoids

4. Parallelograms

5. Kites

6. Rhombuses

Regular quadrilaterals

Of the long list, only a square is a regular quadrilateral. Regular polygons have congruent sides and angles. You can easily see that a rectangle may have four 90° interior angles, but it need not have four equal-length sides.

Irregular quadrilaterals

What is an irregular quadrilateral? Irregular quadrilaterals are: rectangle, trapezoid, parallelogram, kite, and rhombus. They are symmetrical, but are not required to have congruent sides or angles. Do not despair, though, because a few of them yield to area formulas, just as the square does.

In addition to symmetrical, irregular quadrilaterals, other irregular quadrilaterals can exist without symmetry, just four unequal sides:

Area of irregular quadrilaterals

Calculating area (in square units) for a square and rectangle is easy:

• A = Width x Length (W x L), which for a square means the same thing as ${W}^{2}$.

If you have a square with sides 17 cm long, the area is 289 square cm. If you have a rectangle with two sides 17 cm and two sides 34 cm, the area is $17\times 34=578$ square cm.

Calculating area for most of the other irregular quadrilaterals can be tricky. Area of a parallelogram or a rhombus, for instance, is its height (or altitude), not the length of its short side, times its base. With a trapezoid, you have to find the average of the two bases and multiply that times the trapezoid's height.

A kite, which has two adjacent short sides and two adjacent long sides, has an area formula based on its diagonals, d1 and d2:

• $A=\frac{1}{2}(d1\times d2)$

Area of veryirregular quadrilaterals

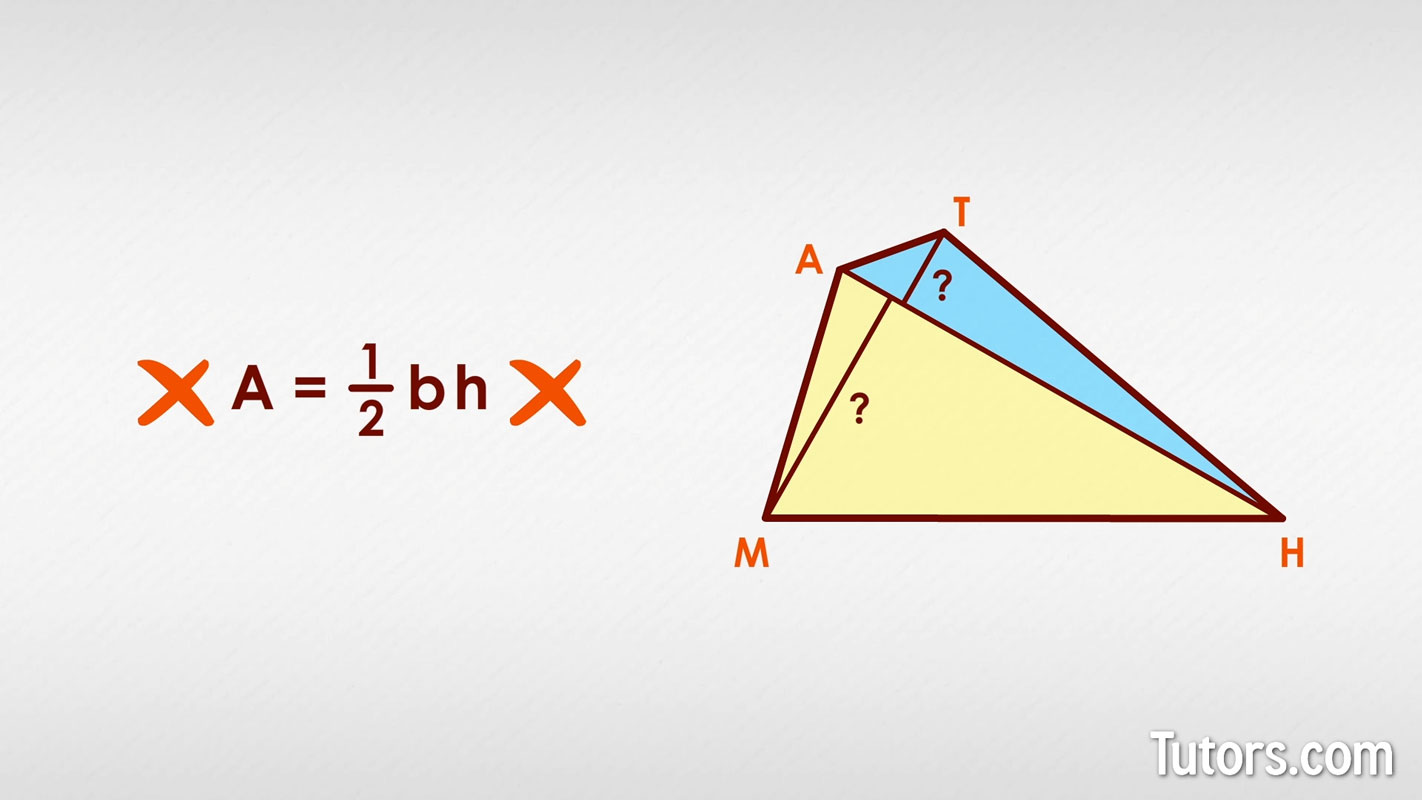
Our earlier example of an irregular quadrilateral, MATH, shows how four sides do not guarantee a symmetrical shape. To find the area of such irregular quadrilaterals, follow a three-step strategy:

1. Divide the quadrilateral into two triangles by constructing a diagonal that does not disturb the known interior angle

2. Calculate the area of each triangle, using formulas

3. Add the areas of the two triangles

For our quadrilateral MATH, connecting the vertex A to vertex H breaks the shape into $\triangle MAH$ and $\triangle ATH$. You do not know the heights, h, of either triangle, so you cannot calculate area using $\frac{1}{2}bh$.

Instead, be a little creative (mathematics is full of creativity) by building one fact on another. In our quadrilateral MATH, if we know one angle, we can use these four steps to find the total area:

1. Knowing that included angle T is 120°, you can use Side-Angle-Side to find the area of $\triangle ATH$

2. Knowing the area of $\triangle ATH$, you can use the Law of Cosines to calculate the unknown length of the diagonal AH

3. Knowing the length of the diagonal AH, you can use Heron's Formula to calculate the area of $\triangle MAH$

4. Knowing the areas of the two triangles, add them to get the area of the irregular quadrilateral

Please notice you must work in sequence, and you must have some basic facts to start. You must know the lengths of the irregular quadrilateral's sides and the measure of one angle. Let's go through each step.

Use side-angle-side

Given the lengths of two sides AT and TH and their included angle T, use the trigonometric function $A=\frac{1}{2}AT\times TH\times \sin\left(T\right)$ to calculate the area of $\triangle ATH$:

Use the law of cosines

We now know the area of $\triangle ATH$, but we do not know the length of diagonal AH. We will use The Law of Cosines:

This Law allows us to calculate the unknown length. We have to recast the formula using our particular labels, keeping in mind in our $\triangle ATH$ the sides can be designated by the lowercase versions of their opposite angles:

• Side AT can be labeled h

• Side TH can be labeled a

• Side AH can be labeled t

We now have the approximate length of side AH as 13.747 cm, so we can use Heron's Formula to calculate the area of the other section of our quadrilateral.

Use Heron's formula

Heron's Formula depends on knowing the semiperimeter, or half the perimeter, of a triangle. For our $\triangle MAH$, the three sides measure:

1. MA = 7 cm

2. AH = 13.747 cm

3. HM = 14 cm

The semiperimeter, s, is half the sum of the sides:

Here is Heron's Formula, where a, b and c are the lengths of the three sides:

Plug in the value s throughout to get your area:

At last, we have the areas of our two triangles. Add them and you have the total area of the irregular quadrilateral:

To the thousandths of a square cm, we have the area of quadrilateral MATH!

Lesson Summary

Now that you have worked your way completely through the lesson, you are able to identify quadrilaterals, distinguish between regular and irregular quadrilaterals, and recall and explain the identifying properties of regular and irregular quadrilaterals. You also can now apply length-times-width as a formula to calculate area of regular and some irregular quadrilaterals, and, when the length-times-width formula cannot apply, find the area of irregular quadrilaterals using other strategies, including using the Law of Cosines and Heron's Formula.