What is Rotational Symmetry? — Definition & Examples
Rotational symmetry
Shapes and objects have rotational symmetry if they can be pivoted (turned or spun) around their center less than one full rotation without appearing to change. Rotational symmetry appears in sea stars, jellyfish, and sea anemones. It also appears in human-made objects like airplane propellers, Ferris wheels, and dartboards.
Center
The center, pivot, or center of balance are all ways to describe the single point on an object around which the object can turn, rotate or spin.
Think of your mathematics textbook. Can you find a spot on it that allows the book to balance on your index finger? When you find that spot, you have the center of the object. The rectangle that is your mathematics textbook can be rotated around that center to find its rotational symmetry.
Rotational symmetry and order
The order of symmetry is a number used to describe how many times the object will appear to be the same while rotating through 360°. If it only matches up twice, it is Order 2; if it matches the original shape three times, it is Order 3, and so on.

Common orders and the amount the object rotates are:
Order 2: 180°
Order 3: 120°
Order 4: 90°
Order 5: 72°
Order 6: 60°
Order 7: between 51° and 52°
Order 8: 45°
Order 9: 40°
Order 10: 36°
You may notice that no Order 1 exists; this would be a shape that has to turn completely around (360°) to look the same. No object has rotational symmetry of Order 1.
You may also notice just how many Orders are possible. This is because 360° has so many factors. The only misfit is Order 7, since 360° does not divide evenly by 7.
Regular polygons
Many everyday objects show rotational symmetry. In mathematics, all the regular polygons have rotational symmetry.
Here is an equilateral triangle. How many times will it match itself when rotated around its center?
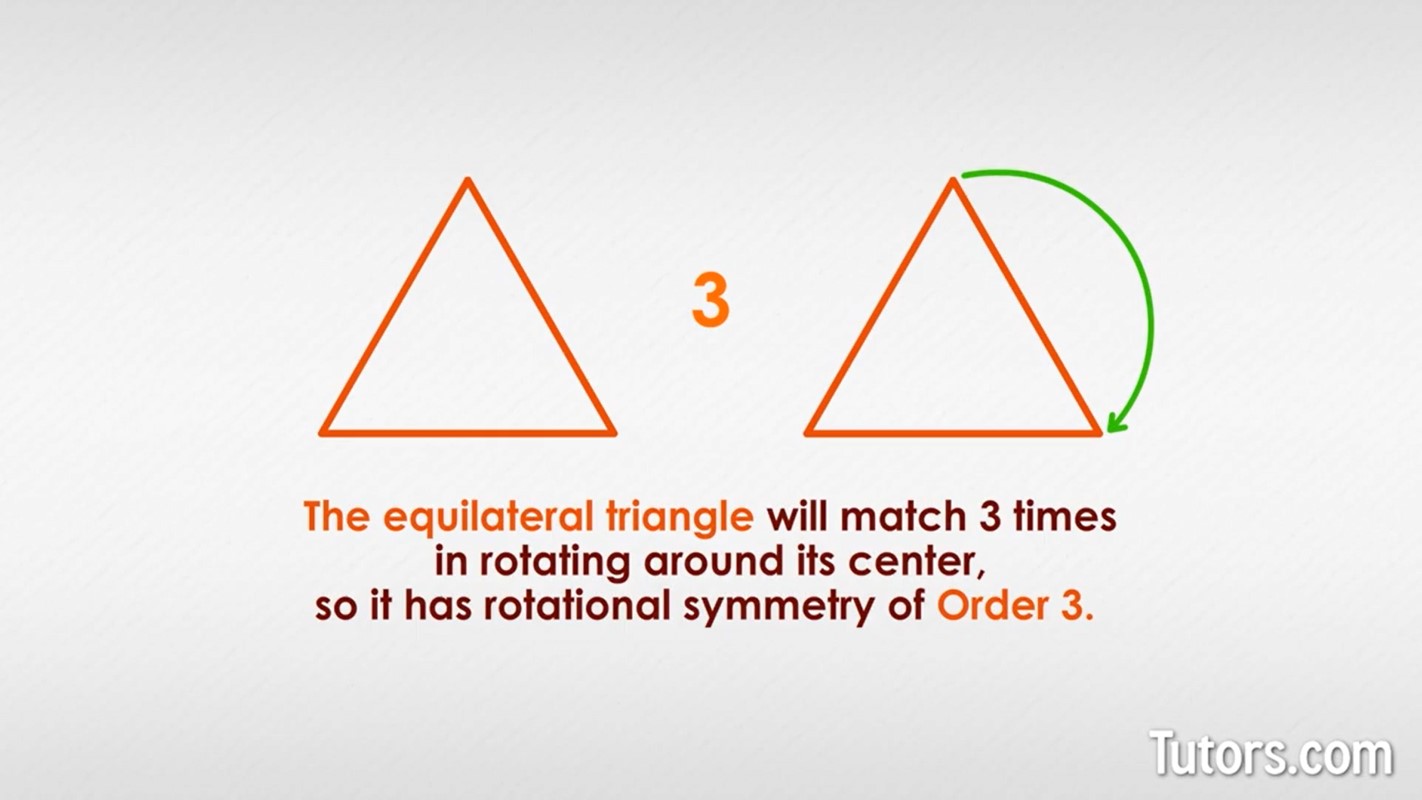
The equilateral triangle will match three times in rotating (turning) around its center. So it has rotational symmetry of Order 3.
Can you figure out the Order of rotational symmetry for the square below?
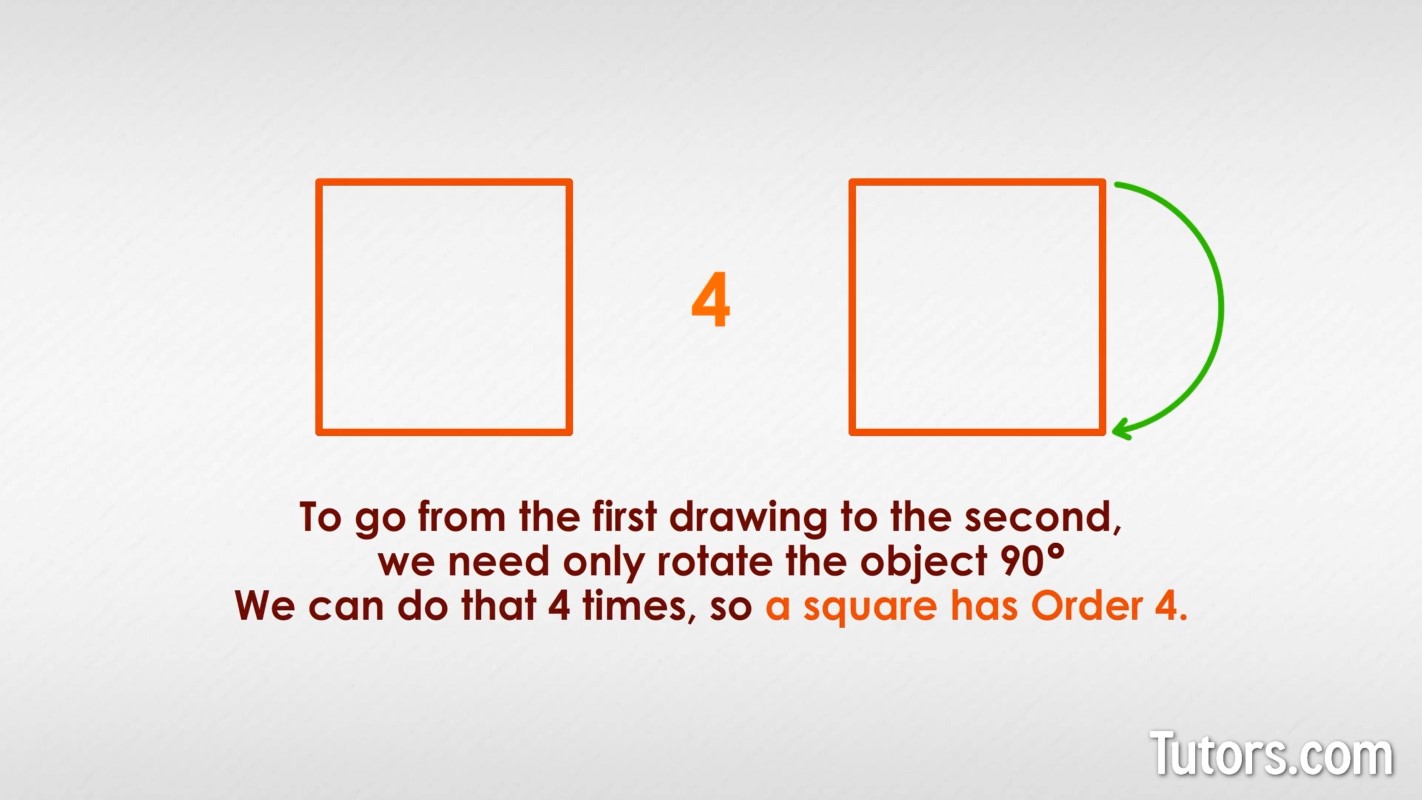
To go from the first drawing to the second, we need only rotate the object 90°. We can do that four times, so a square has Order 4.
What about this regular pentagon? What is its rotational symmetry?
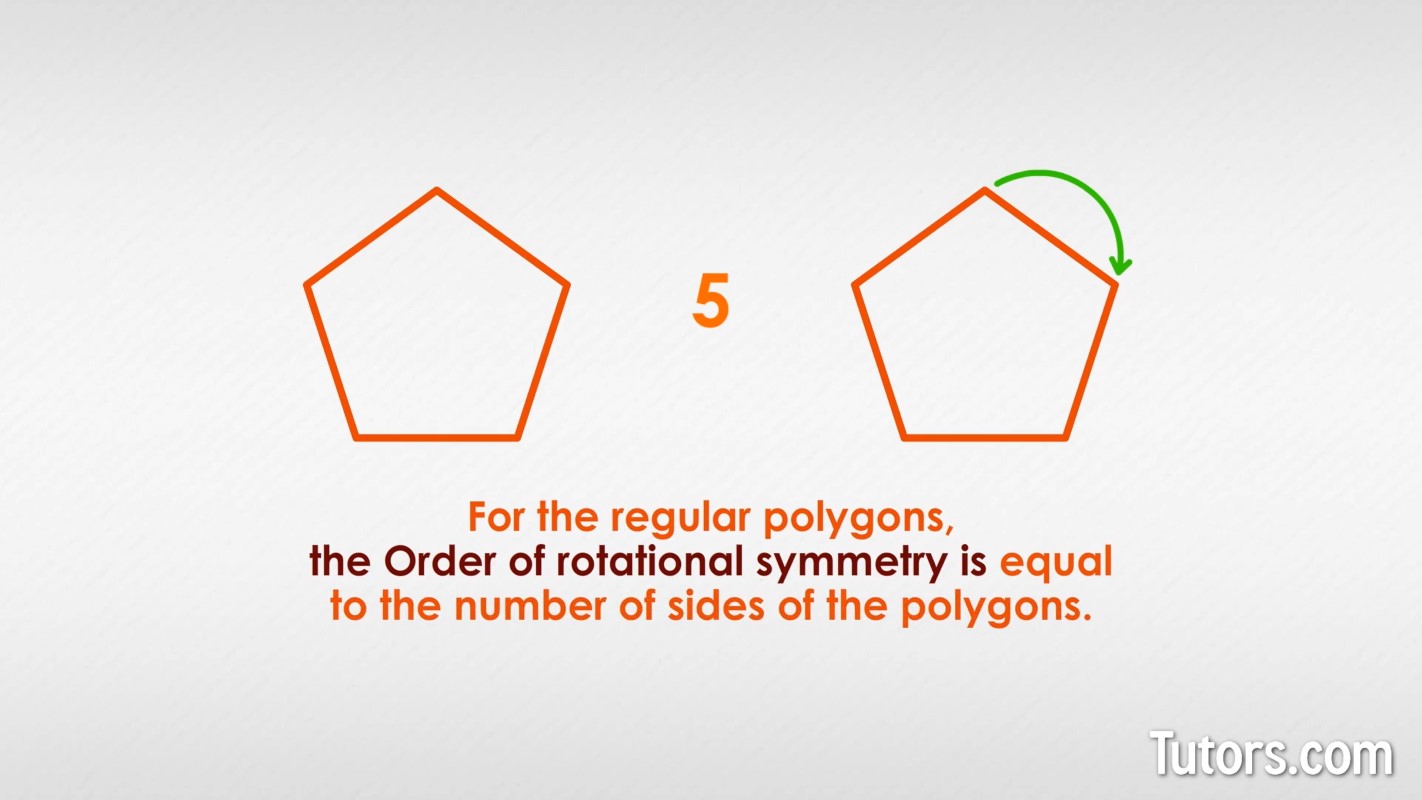
Did you say it is Order 5? Have you noticed a pattern? For the regular polygons, the Order of rotational symmetry is equal to the number of sides of the polygons.
Without drawing it, can you say what the Order of rotational symmetry is for a regular decagon, a 10-sided polygon? It is Order 10, meaning you can rotate the figure 36° and match it to the original. You can do that 10 times in making one complete rotation.
Degree of rotation
The number of degrees you must rotate the object around its center is key to finding its Order of rotational symmetry, but it also tells you how much to rotate the object to make it match its original position.
Very often you can find the degrees of rotation by physically rotating the object, if it is something in your daily life. Take a rectangular cell phone, for example. Concentrating only on its outline, what happens when you rotate (spin) the phone halfway around a complete circle?

You can do that same move again to return to the original shape. So, the cell phone's rectangular shape rotated 180° two times; Order 2.
You can get the degree of rotation if you know the Order, by dividing:
= degree of rotation
You can get the Order if you know the degree of rotation, by dividing:
= order
Getting back to our sea stars, can you figure out their Order of rotational symmetry and their degrees of rotation? Remember, a sea star has five arms.
The sea star is Order 5, using 72 degrees of rotation.
Picture a hexagonal shape, like a honeycomb or a section of a soccer ball. Can you name its Order and degrees of rotation?
A hexagon shows Order 6 rotational symmetry, with 60 degrees of rotation.