What is a Cuboid? - Definition, Shape, Area & Properties

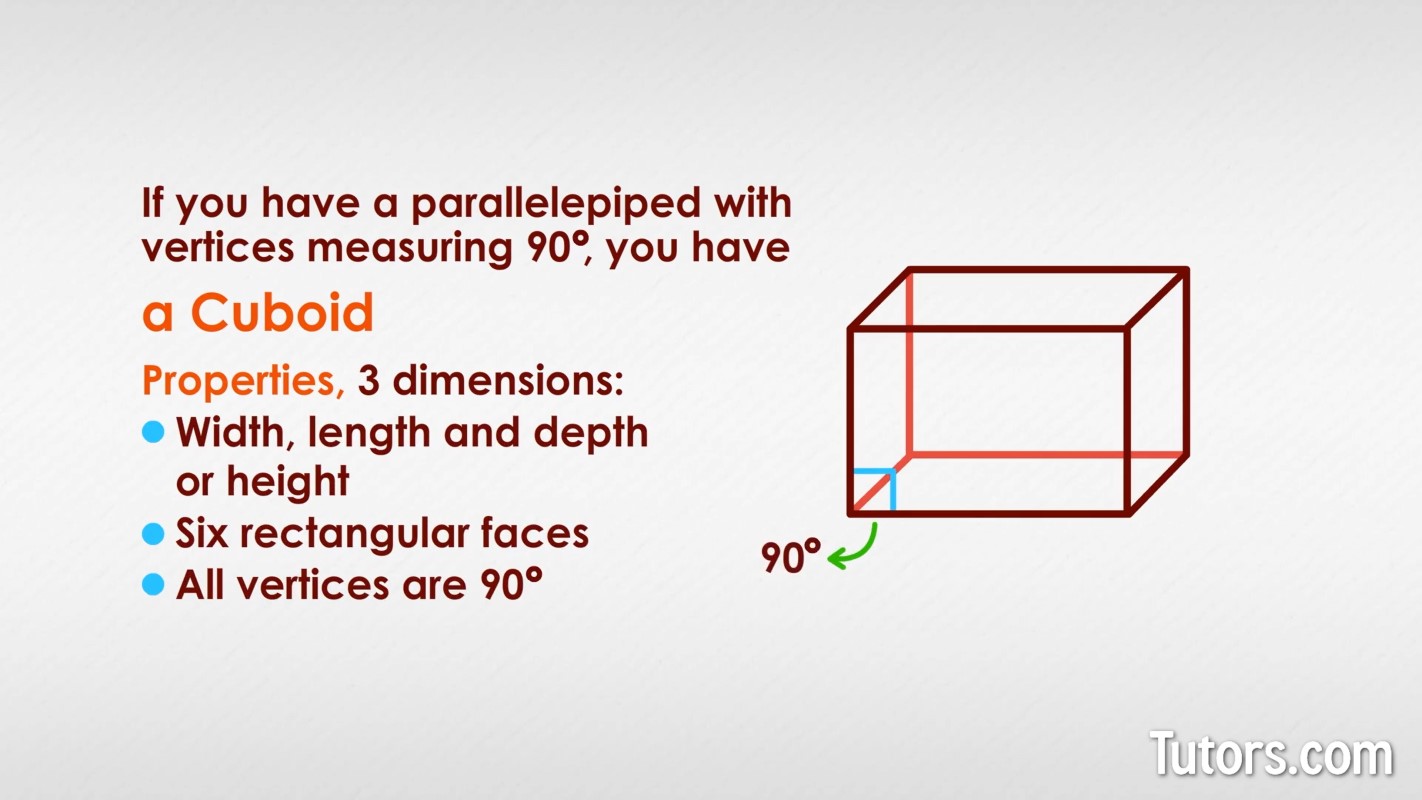
A cuboid is not a cube. A cube can be a cuboid, but so can a rectangular prism. A cuboid is a special case of a parallelepiped, a three-dimensional solid with six parallelogram-shaped faces. A shoebox is a cuboid. A pair of dice, building bricks, and hardbound textbooks are all cuboids. Books, cardboard cartons, and Klondike® ice cream bars are cuboids. If the 3D object has six parallelograms all meeting at right angles, it is a cuboid.

Table Of Contents

1. Parallelogram
2. Parallelepiped
3. Cuboid
4. Properties of Cuboids
5. Calculating Volume of Cuboids
6. Try It!
7. Surface Area of Cuboids
8. Example Problems!

Parallelogram

A parallelogram is a polygon with two pairs of parallel sides. So, rectangles and squares are parallelograms:

[insert drawing of square, obviously leaning parallelogram, and rectangle]

Parallelepiped

If you assemble six parallelograms to form a three-dimensional solid, you have a polyhedron called a parallelepiped:

[insert drawing of parallelepiped with obviously leaning sides]

Another name for this three-dimensional shape is a rectangular prism or right prism.

Cuboid

If you have a parallelepiped with vertices measuring 90°, you have a cuboid:

[insert drawing of cuboid; OR, instead of those three drawings, consider a video that transforms a parallelogram into a 3D leaning box shape, and then straightens up to make a shoebox shape with right angle corners]

Properties of Cuboids

All cuboids have these properties:

1. Three dimensions of width, length and depth (or height)
2. Six rectangular faces
3. All vertices are 90°

These three properties mean opposite sides of the cuboid are parallel and congruent to each other.

These conditions result in a box shape, like a shoebox, cereal box, or a textbook.

Calculating Volume of Cuboids

To find the volume of any cuboid, the formula is:

• V = length x width x height (or depth)
• V = lwh

Because the object is three-dimensional, volume is expressed as a cube -- the third power -- of whatever linear unit you used: cubic meters, cubic feet, cubic yards, and so on.

Try It!

Here is a shipping container, the kind you see stacked like children's blocks on cargo ships:

[insert copyright-free photograph of a 40-foot shipping container]

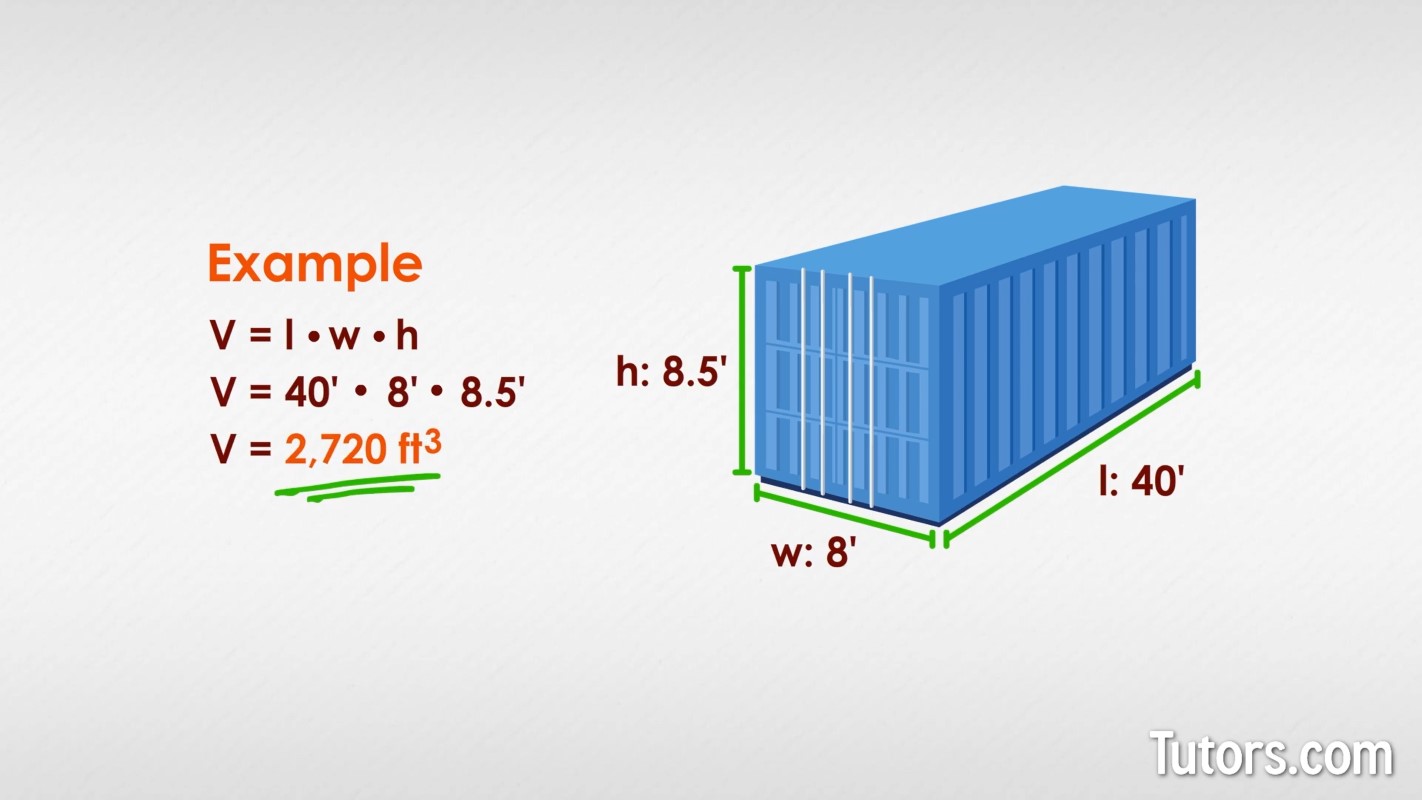
The outside dimensions are 8' wide, 8.5' high, and 40' long. What is the volume of the container?

• V = lwh
• V = 8' x 8.5' x 40'
• V = 2,720 cubic feet

Surface Area of Cuboids

To calculate the surface area of any cuboid, you need to know the surface area of each face. You then add all six areas together.

Because opposite faces are congruent, you only need three faces, which you can multiply times two and then add together. You are using each dimension (width, length, and height or depth) two and only two times in the formula.

The formula is:

• SA = 2lw + 2wh + 2lh

Surface area is always measured in square units of the linear measurement, the second power.

Here is a box for cowboy boots:

[insert cartoon drawing of big shoebox with cowboy boots standing beside it]

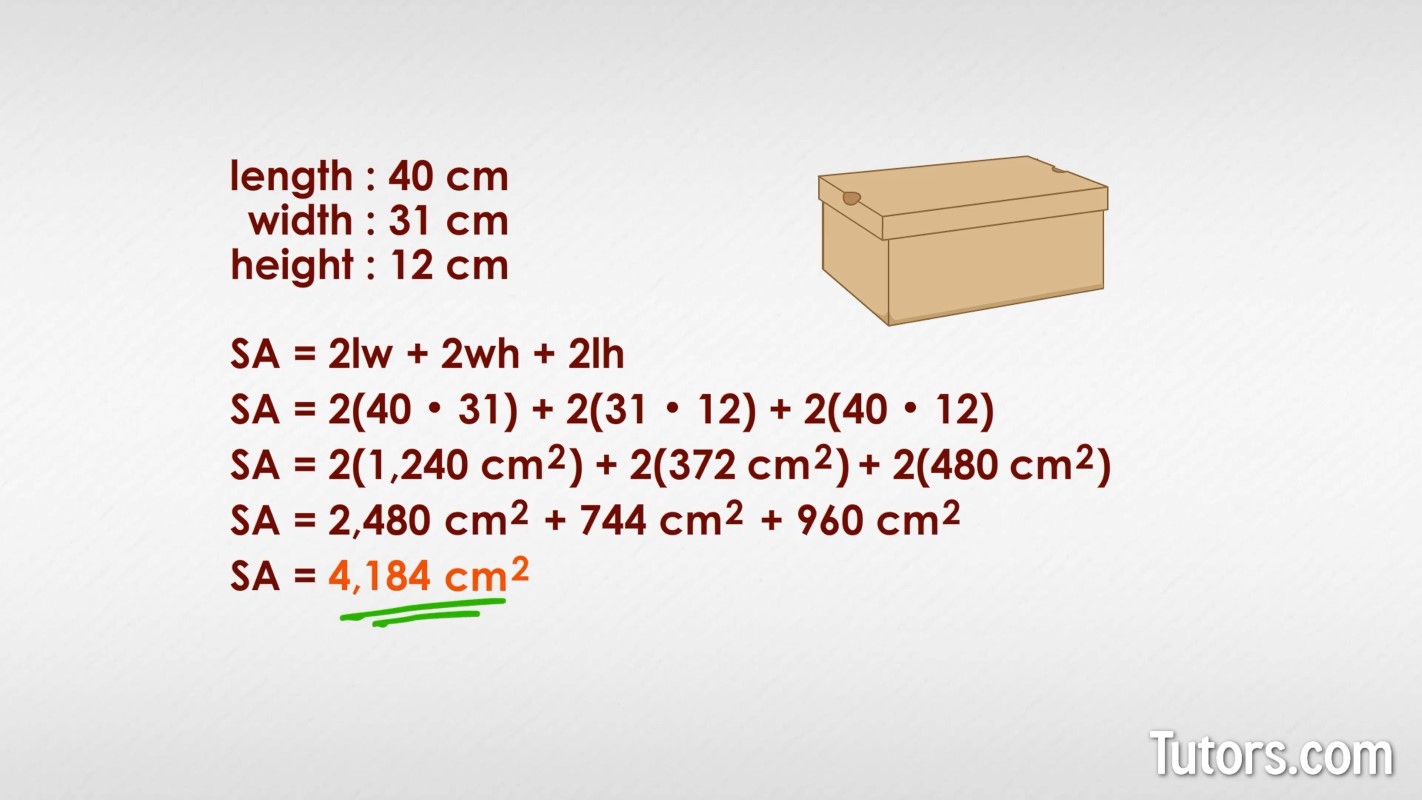
The box measures 40 cm long, 31 cm wide and 12 cm high. You have to wrap these boots for a present. You need gift wrap. What is the total surface area of the box, in square centimeters, so you buy enough gift wrap?

• SA = 2lw + 2wh + 2lh
• SA = 2(40 x 31) + 2(31 x 12) + 2(40 x 12)
• SA = 2(1,240 cm^2) + 2(372 cm^2) + 2(480 cm^2)
• SA = 2,480 cm^2 + 744 cm^2 + 960 cm^2
• SA = 4,184 cm^2

Example Problems!

The decorative storage box you use to hold all your Mathematics competition trophies and ribbons measures 12" long x 8.5" wide x 6" tall on the inside. You want to line the inside with contact paper for protection. How many square inches of contact paper will you need?

• SA = 2lw + 2wh + 2lh
• SA = 2(12 x 8.5 in.^2) + 2(8.5 x 6 in.^2) + 2(12 x 6 in.^2)
• SA = 2(102 in.^2) + 2(51 in.^2) + 2(72 in.^2)
• SA = 204 in.^2 + 102 in.^2 + 144 in.^2
• SA = 450 in.^2

Your Math Club is sending rescued mathematics textbooks to needy schools in Africa. Calculate the interior volume of a half-length shipping container with these interior dimensions:

• Length: 5.89 m
• Width: 2.35 m
• Height: 2.36 m
• V = lwh
• V = 5.89 m x 2.35 m x 2.36 m
• V = 32.66594 m^3

A cuboid is a rectangular prism, a parallelepiped with 90° vertices (corners). Cuboids are everywhere: bricks, buildings, ice cream sandwiches, textbooks, shoeboxes, game dice, shipping containers, cereal boxes, and in many other corners of your world. You can easily calculate both the surface area and volume of any cuboid, if you know its width, length and height (or depth).

Next Lesson:

Dodecagon