Similarity Transformations
Similarity and transformations
You love your dog Bailey. Imagine you are told that a small dog, Buddy, in your neighborhood looks exactly like your own big dog Bailey. You are interested in seeing Bailey and Buddy side by side to compare them, but your dog is curled up, asleep on the couch, and the other dog is down the block. What can you do?
You could bring Bailey and Buddy together. You would have to wake Bailey up and get the two dogs facing the same direction, so you could compare snouts, and ears, and tails.
Our example may sound a bit silly, but in geometry we use transformations all the time to bring two objects near each other, turn them to face the same way, and, if necessary, flip them to see if they are similar.
What is similarity?
Two geometric shapes are similar if they have the same shape but are different in size. A shoe box for a size 4 child's shoe may be similar to, but smaller than, a shoe box for a man's size 14 shoe. Or like your dog Bailey and the neighborhood dog Buddy.
Congruent objects are also similar, but similar objects are not congruent.
Are they similar?
Below are two isosceles triangles, one with sides twice as long as the other. Are they similar? You have to check their interior angles to see if they are the same in both isosceles triangles. You check and the corresponding angles between legs and third sides are congruent, at 71°.
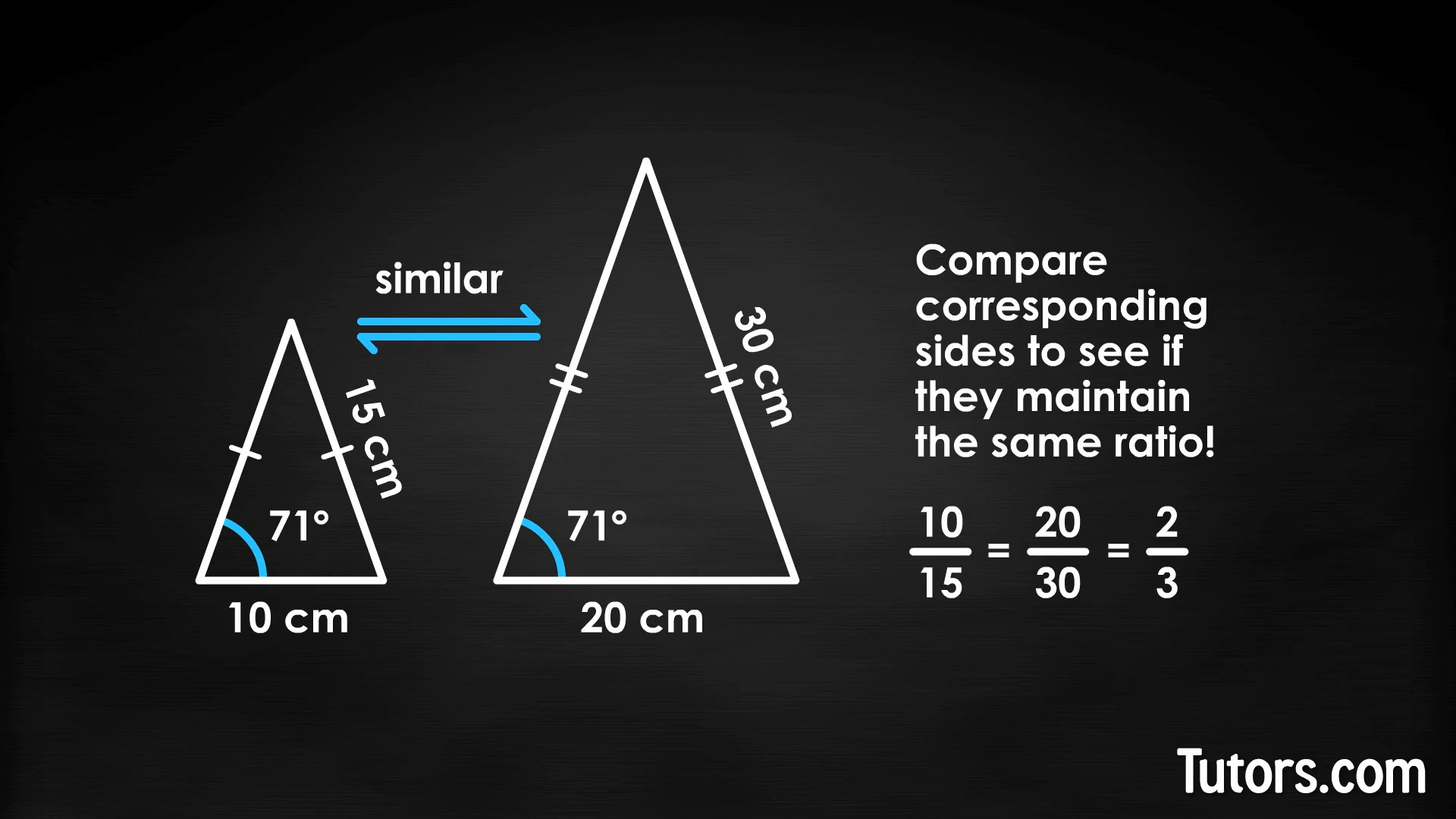
Next, you have to compare corresponding sides to see if they maintain the same ratio. Recall that the equal sides of an isosceles triangle are called legs. Notice the left triangle has two legs 15 cm long and a third side, 10 cm long. The right triangle has 30 cm legs and a 20 cm third side.
If the ratio of one side and one leg of the left-hand triangle is the same ratio as the corresponding side and leg of the right-hand triangle, they are proportional to each other, so they are similar. So are these ratios the same?
Yes; the proportions of the two isosceles triangles are the same, so the two triangles are similar.

Congruent
Polygons (or any geometric shapes) are congruent if they are the same size and shape. Two equilateral triangles, each with one side 90 meters long, are congruent. Two 6-inch circles are congruent.
What is a similarity transformation?
Geometry transformations are movements of two-dimensional shapes in two dimensions, or within their plane. Like restricted game pieces on a game board, you can move two-dimensional shapes in only three ways:
Rotation – Shapes are rotated or turned around an axis
Reflection – Shapes are flipped across an imaginary line to make mirror images
Translation – Shapes are slid across the plane

You use all of these concepts in everyday life. Let's check each out separately.
Rotation
The scalene triangle on the left and the scalene triangle on the right are actually similar, but the one on the right has been rotated to stand on its shortest side.
To see if the two triangles are similar, you first have to get them both in the same direction, or orientation. You do this by rotating (turning) one shape to align with the other. Such a transformation is called a rotation.

Reflection
With regular polygons, you cannot tell if a figure has been reflected, since all sides are equal and all angles are equal. One square will look like another. They may be different sizes but the same shape, so they are all similar.
With some irregular polygons, some reflections leave you with an identical shape. Most irregular polygons, thought, will look very different once you reflect them or flip them.
Here are two long, narrow rectangles. They are not regular quadrilaterals, so you can easily see that two sides are much longer than the other sides. Can you tell if one rectangle is a reflection of the other?
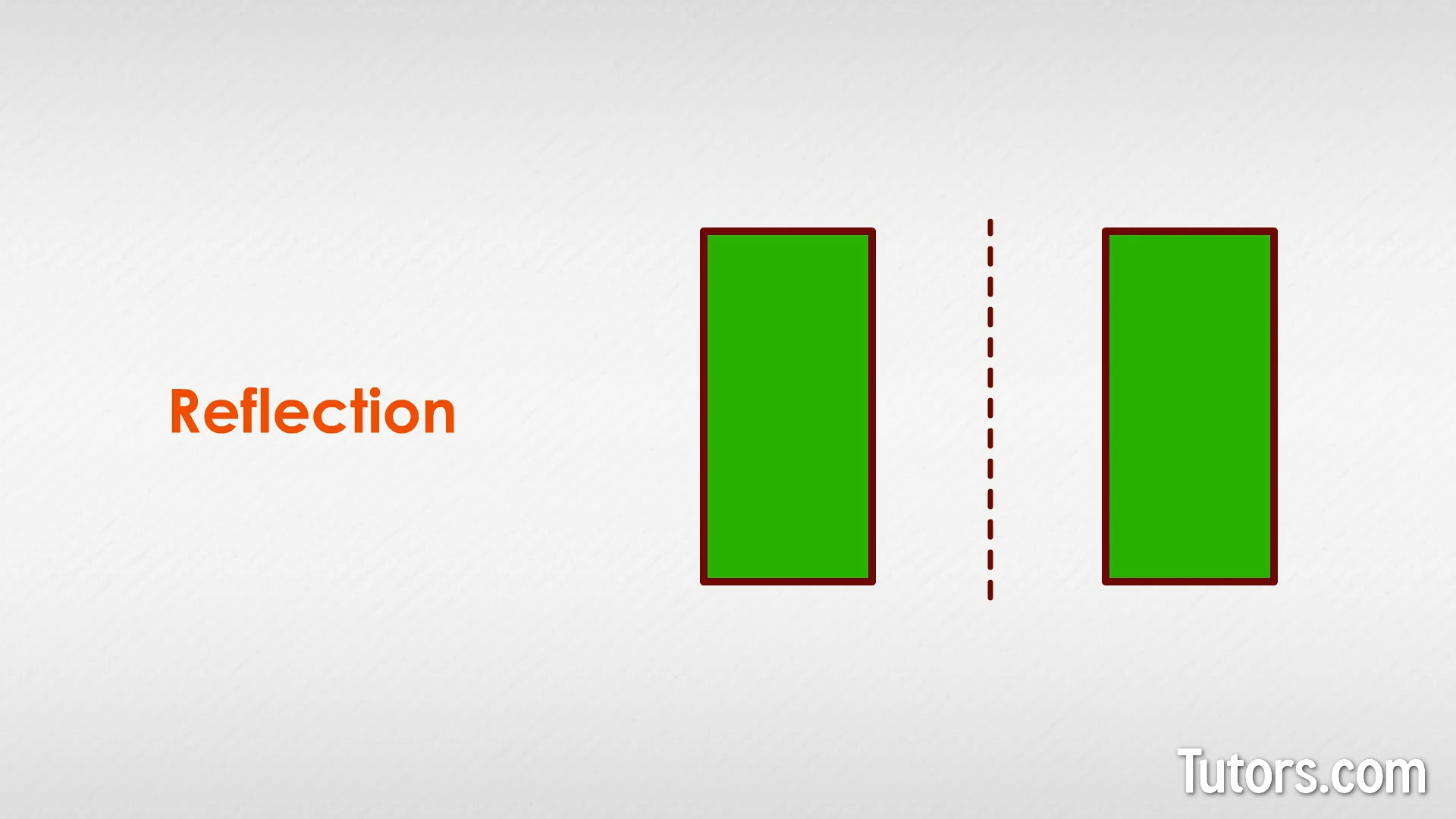
No, you cannot, because when you reflect this rectangle either horizontally or vertically, the rectangle appears the same.
Now look at this irregular trapezoid, with two interior angles forming right angles. It is called a right trapezoid because of those two right angles.
If we imagine a vertical line to the right of the shape, we can flip or reflect the shape across that line, as if we picked it up, turned it over like a pancake, and put it down on the right.

Now the short side of the newly placed trapezoid is facing the corresponding short side of the original. The new trapezoid is reflected; the image is a reflection.
Translation
If you are shown a polygon and its translation, you may think you are looking at the same polygon twice. Translating a shape means moving it around on the plane the shape is in; you slide it, without changing its orientation (you do not rotate it).

Translations are handy in bringing two shapes together to evaluate to see if they are similar or not. When they are far apart (like the two dogs), you have a hard time comparing corresponding parts.
Similarity transformation examples
Below are two rectangles, spaced far apart and in different orientations. Rectangles BATH has long sides of 30 yards and short sides of 21 yards. MUCK have long sides of 40 yards and short sides of 28 yards. You need not worry about corresponding interior angles (they are all 90°).
Notice MUCK is bigger than BATH, which means the two rectangles cannot be congruent. Because they are oriented in different ways, you cannot easily tell if they are similar. What will you do?
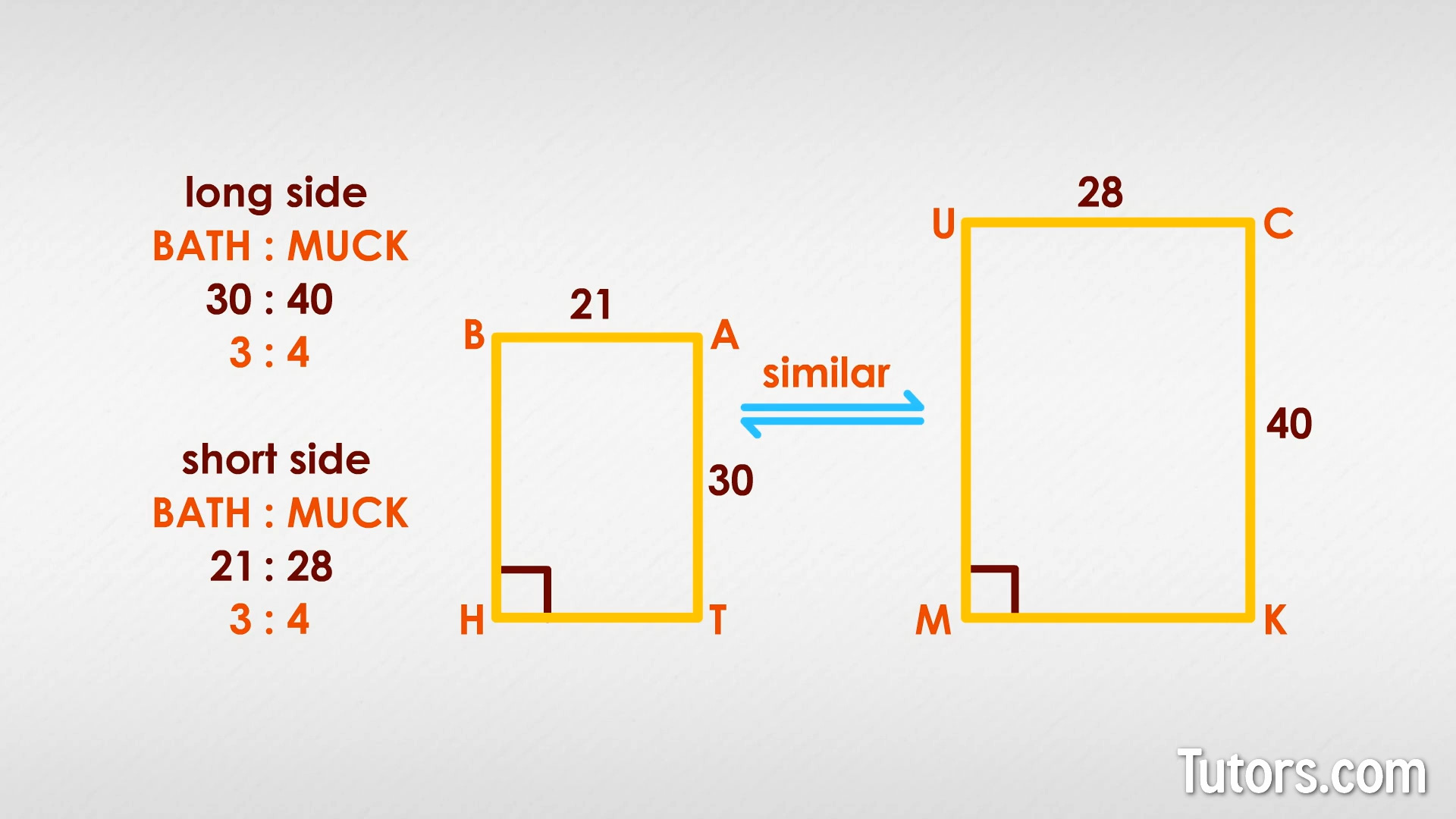
If you said you would rotate and then translate (or the other way around) the two rectangles, you are correct. Once you get them near each other and in the same orientation on the page, you can compare the two using corresponding parts:
BATH's long side compared to MUCK's long side is
BATH's short side compared to MUCK's short side is
Are those two ratios the same? Yes, they both simplify to , so the two rectangles are similar to each other. We chose the easiest ratios to compare, but you could also have compared BATH's length and width to MUCK's length and width:
BATH's short side and long side
MUCK's short side and long side
These are a bit harder, but still reduce to . The two rectangles are similar.
Example #2
Was that too easy? Here are two shapes that look a little like New England Saltbox houses from Colonial times. We will call our pentagons QUACK and SDRIB. Are they similar? What will you do to find out? Because these irregular pentagons are very irregular and far apart, you have to do a lot of transformations.
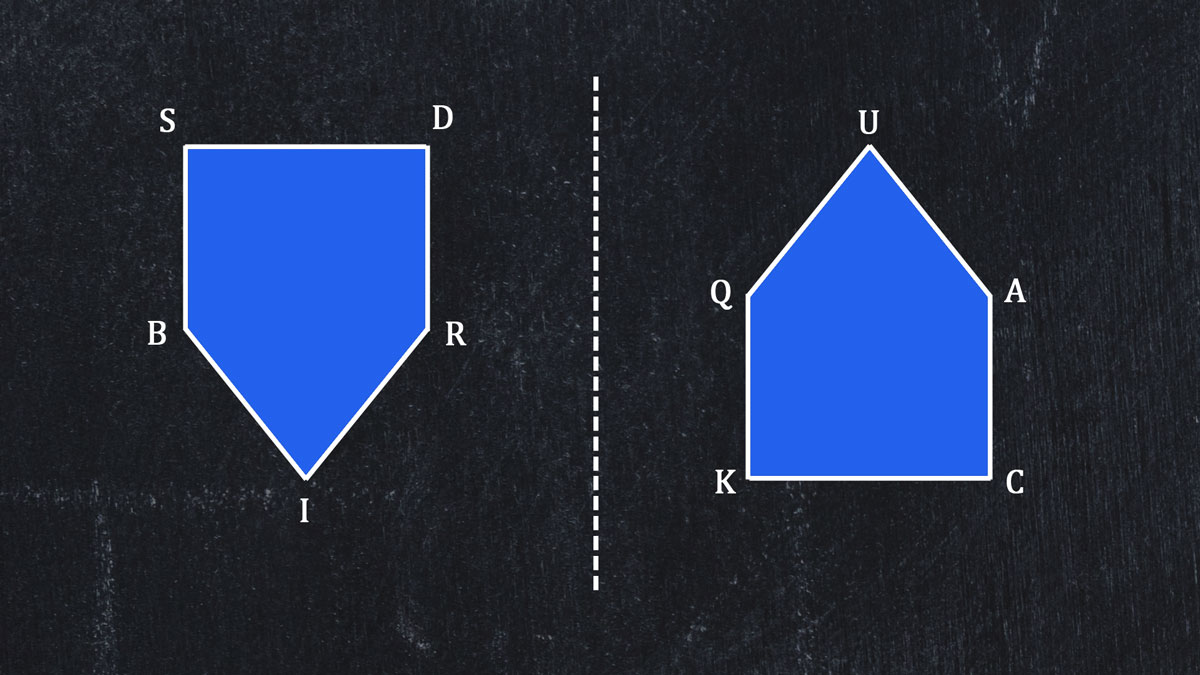
Rotate SDRIB so its longest side is oriented to match QUACK's longest side.
Reflect SDRIB so it has the long slope on the left, just like QUACK.
Translate the two shapes so they are near each other.
Now you have, from left to right, BIRDS QUACK. Compare corresponding parts. Even though BIRDS is smaller than QUACK, all their angles match; their sides are in proportion; they are similar.
Lesson summary
Now that you have worked through this lesson, you are now able to remember what "similar" and "congruent" mean, describe three geometry transformations (rotation, reflection, and translation), and apply the three transformations to compare polygons to determine similarity or congruence.
You also know that similar shapes differ in size only, and congruent shapes have congruent interior angles and congruent lengths of sides. You also learned that congruent shapes are also similar, but not all similar shapes are congruent.