Pythagorean Triples

Table of Contents

1. Pythagorean Triple Definition
2. Pythagorean Triples
• Primitive Pythagorean Triples
• How To Find Pythagorean Triples
3. Pythagorean Triples Formula
4. Pythagorean Triples Examples
5. Generating Pythagorean Triples
6. Pythagorean Triples List

What Is A Pythagorean Triple?

Some numbers seem to work perfectly in the Pythagorean Theorem, like 3, 4, and 5, which is 3² + 4² = 5². Sets of positive, whole numbers that work in the Pythagorean Theorem are called Pythagorean triples.

For three positive integers to be Pythagorean triples, they must work in the Pythagorean Theorem's formula:

In the Pythagorean Theorem's formula, $a$ and $b$ are legs of a right triangle, and $c$ is the hypotenuse.

Only positive integers can be Pythagorean triples. The smallest Pythagorean triple is our example: (3, 4, and 5).

A quick way to find more Pythagorean triples is to multiply all the original terms by another positive integer:

$\times 2: (6, 8, 10)$

$\times 3: (9, 12, 15)$

$\times 4: (12, 16, 20)$

$\times 5: (15, 20, 25)$

Pythagorean Triples

Pythagorean triples are relatively prime. Relatively prime means they have no common divisor other than 1, even if the numbers are not prime numbers, like 14 and 15. The number 14 has factors 1, 2, 7, and 14; the number 15 has factors 1, 3, 5, and 15. Their only common factor is 1.

Primitive Pythagorean Triples

A set of numbers is considered to be a primitive Pythagorean triple if the three numbers have no common divisor other than 1.

Our first Pythagorean triple is primitive, since (3, 4, and 5) have no common divisors other than 1. Our fifth set from our example above, however, is not primitive (it is imprimitive) because each value for a, b, and c of the right triangle is a multiple of 5.

How To Find Pythagorean Triples

Here's how to find Pythagorean triples in three easy steps:

1. Pick an even number to be the longer leg's length.
2. Find a prime number one greater than that even number, to be the hypotenuse.
3. Calculate the third value to find the Pythagorean triple.

Pythagorean Triples Formula

Suppose you pick 12 as the length of a leg, knowing 13 is an adjacent prime number. Use these two as part of the Pythagorean Theorem to complete your primitive Pythagorean triple:

$a^2 + b^2 = c^2$

$a^2 + {12}^2 = {13}^2$

$a^2 + 144 = 169$

Subtract the value of $b^2$ from both sides:

$a^2 + (144 - 144) = (169 - 144)$

$a^2 = 25$

$\sqrt{a^2} = \sqrt{25}$

$a = 5$

So our primitive Pythagorean triple is (5, 12, 13)! You can quickly generate iterations of that (none of which will be primitive) using the same multiplying method we used before: (10, 24, 26); (15, 36, 39); and so on.

Pythagorean Triples Examples

Generate a primitive Pythagorean triple based on the prime number 41. What even number is adjacent to and smaller than 41?

$a^2 + b^2 = c^2$

$a^2 + {40}^2 = {41}^2$

$a^2 + \mathrm{1,600} = \mathrm{1,681}$

$a^2 + (\mathrm{1,600} - \mathrm{1,600}) = (\mathrm{1,681} - \mathrm{1,600})$

$a^2 = 81$

$\sqrt{a^2} = \sqrt{81}$

$a = 9$

Did you get $a = 9$, $b = 40$, and $c = 41$? The primitive Pythagorean triple is (9, 40, 41).

Generating Pythagorean Triples

You can come up with your own Pythagorean triples. Label two positive integers $m$ and $n$, ensuring $m > n$. Then, for each side of a right triangle:

$a = m^2 - n^2$

$b = 2 \times n \times m$

$c = n^2 + m^2$

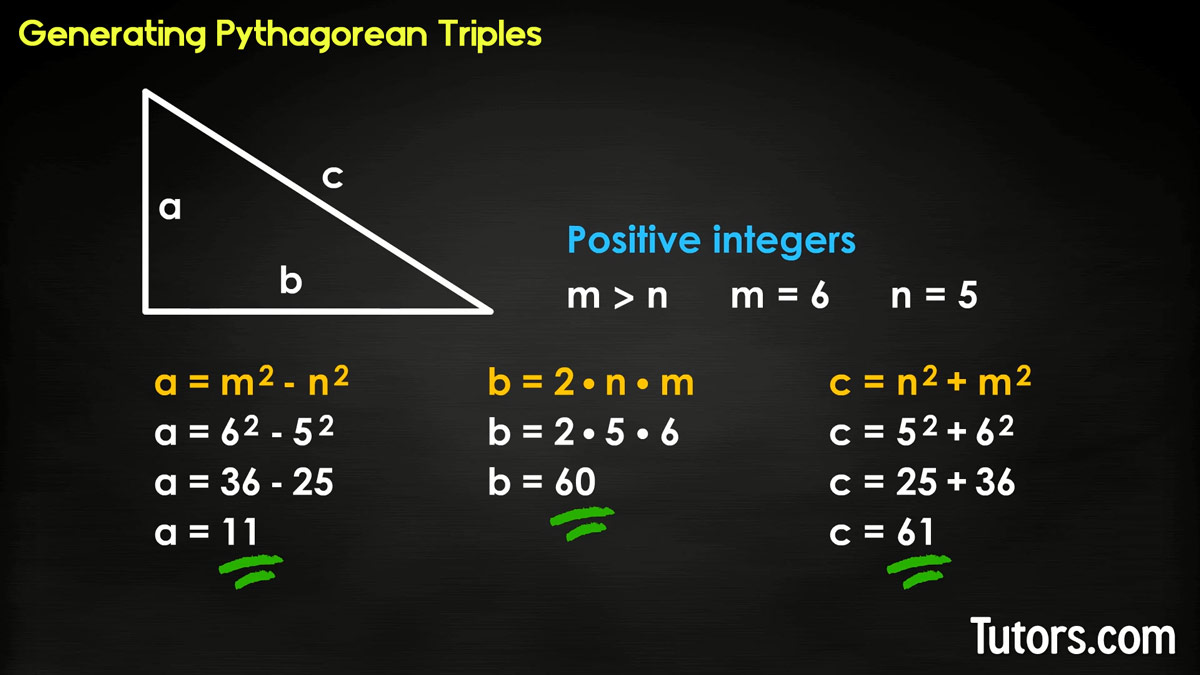
Formula For Generating Pythagorean Triples

Generate a set of Pythagorean triples for $m = 6$ and $n = 5$ using our formula:

Let's solve for a:

$a = m^2 - n^2$

$a = 6^2 - 5^2$

$a = 36 - 25$

$a = 11$

Now, let's solve for b:

$b = 2 \times n \times m$

$b = 2 \times 5 \times 6$

$b = 60$

And finally, c:

$c = n^2 + m^2$

$c = 5^2 + 6^2$

$c = 25 + 36$

$c = 61$

Our Pythagorean triple is (11, 60, 61). This method catches primitive and imprimitive Pythagorean triples.

Pythagorean Triples List

I know many of you are eager to get your hands on a Pythagorean Triples list already pre-computed for you. Here's a list of some common ones:

Lesson Summary

By watching the video, reading the lesson, and studying the formulas, you have learned how to identify a Pythagorean triple, apply and use the Pythagorean Theorem (3² + 4² = 5²), classify a Pythagorean triple as either primitive or imprimitive, and use both the Pythagorean Theorem and another method to find Pythagorean triples.

Next Lesson:

What is a Polygon?