How to Solve Proportions
What are proportions?
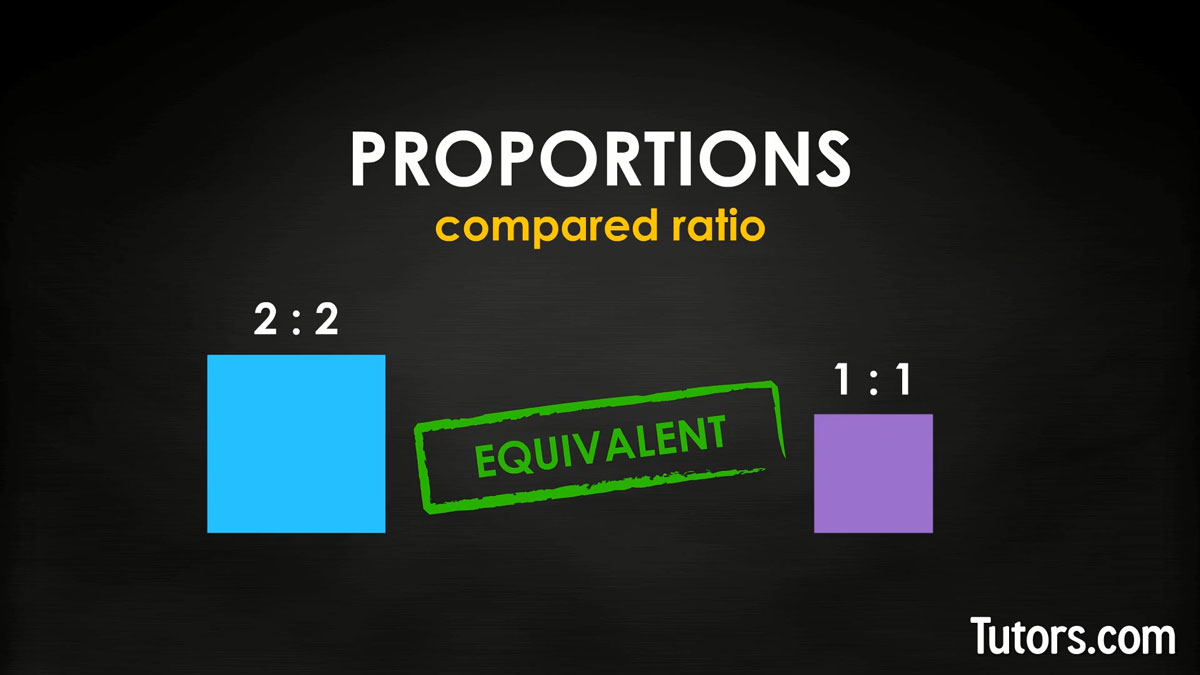
A proportion is a compared ratio. Usually you are ensuring that a given ratio is equivalent to another ratio by seeing if the two ratios are proportional. That is, whatever the dimensions are of one object, another object's dimensions are scaled up or down to maintain the same ratio of height to length, for example.
Ratios can be equivalent or not equivalent. Ratios that are not equivalent could be larger or smaller than one another. Ratios that are equivalent are said to be in proportion, or proportional.
You work with proportions when making images larger and smaller, finding unknown lengths of objects, cooking, and making scale models.
How to solve proportions
To make sure things stay in proportion while increasing or decreasing their size, be sure to multiply all the numbers in the original ratio by the same amount.
For example, if I was making brownies I would use a ratio of 1 cup of flour to 1 cup of sugar which is a ratio of 1:1.
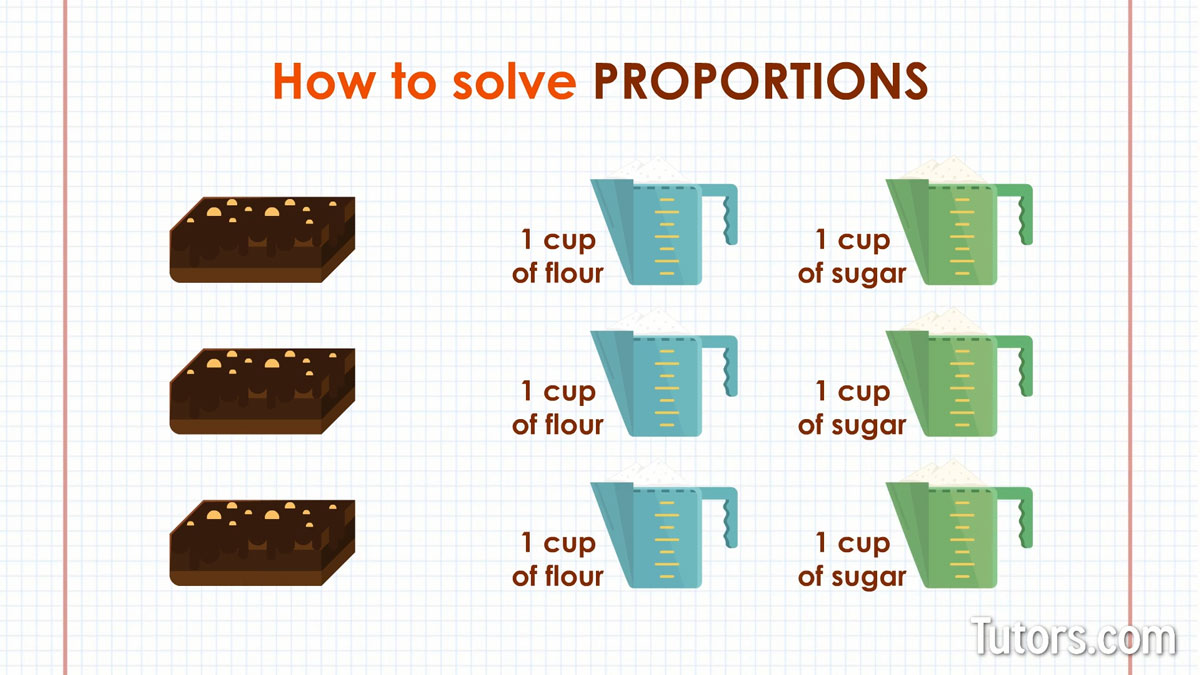
If I wanted to triple the amount of brownies and keep the recipe the same, I would multiply each number in the ratio by 3. This would bring our ratio to 3:3 and means I would need 3 cups of flour and 3 cups of sugar to make triple the amount of brownies.
Let's take a look at an example. The ratios 2:5 and 6:15 are proportional because both divide into the same number:
What about the ratios 4:10 and 5:10? Let's see:

These ratios are not proportional because they don't divide into the same number
Solving proportions examples
Recipes
A recipe for 24 (two dozen) cookies needs 1 cup of flour. To scale the recipe up to make 12 dozen cookies, how much flour do you need?
Set up your proportions comparing 24 and 144 cookies, or (more easily) two dozen and 12 dozen cookies:
2 dozen cookies: 1 cup of flour = 12 dozen cookies: x cups of flour
Look at the relationship between the two numerators in our fractional proportions. What do you multiply 2 times to get 12?
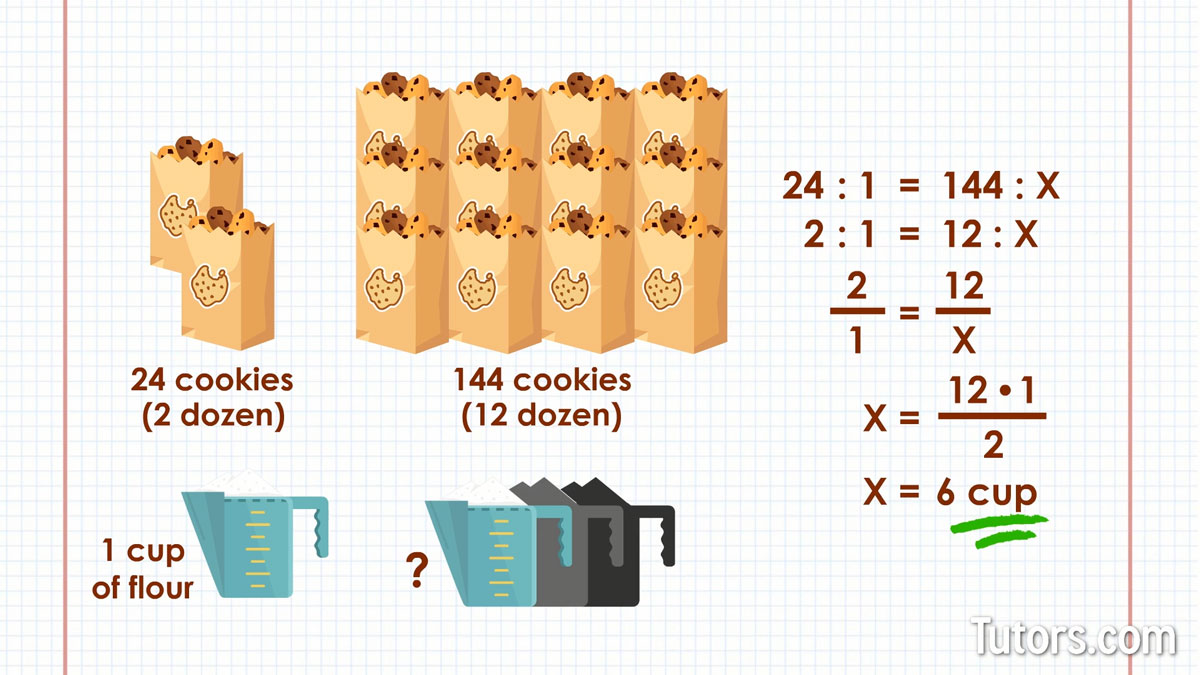
You multiply it times 6, so you multiply the denominator 1, times 6.
You need 6 cups of flour to make 12 dozen cookies.
Photography
A common American size of photograph for framing is a 5" x 7", often written as shorthand as 5×7. If you want another version of the same photograph without cropping (cutting), you can get all these that are in the same proportion (ratio of height to length) by multiplying:
Multiply by 2:
Multiply by 3:
Multiply by 4:
Graphic arts
Another common proportion is poster sizes. You may have a tiny picture that is 2x3, but that could be available in all these sizes, all in proportion to one another:
4×6
8×12
10×15
12×18
16×24
20×30
You often see these dimensions used for electronics as "aspect ratios," so a perfect image on a laptop is not cut off when viewed on a tablet or smart phone.
Scale models
Proportions are used in constructing scale models for hobbyists, architects, engineers, and scientists. Models are easy to examine, as they are usually much smaller than the real object.

Models are lightweight and portable and can help with decisions before expensive, real objects are constructed. An architectural model of a building may be in a scale so that 1" on the model is the same as 12" in real life, so the model has a ratio of 1:12, or 1/12th scale.
Suppose you have a model of an experimental aircraft. The model is 1/100th or 1:100 scale. One centimeter on the model equals 100 centimeters (or 1 meter) on the real aircraft.
You measure the model's cockpit canopy (the plastic shield over the pilot) and see it is 2 centimeters. How long will that be on the actual aircraft?
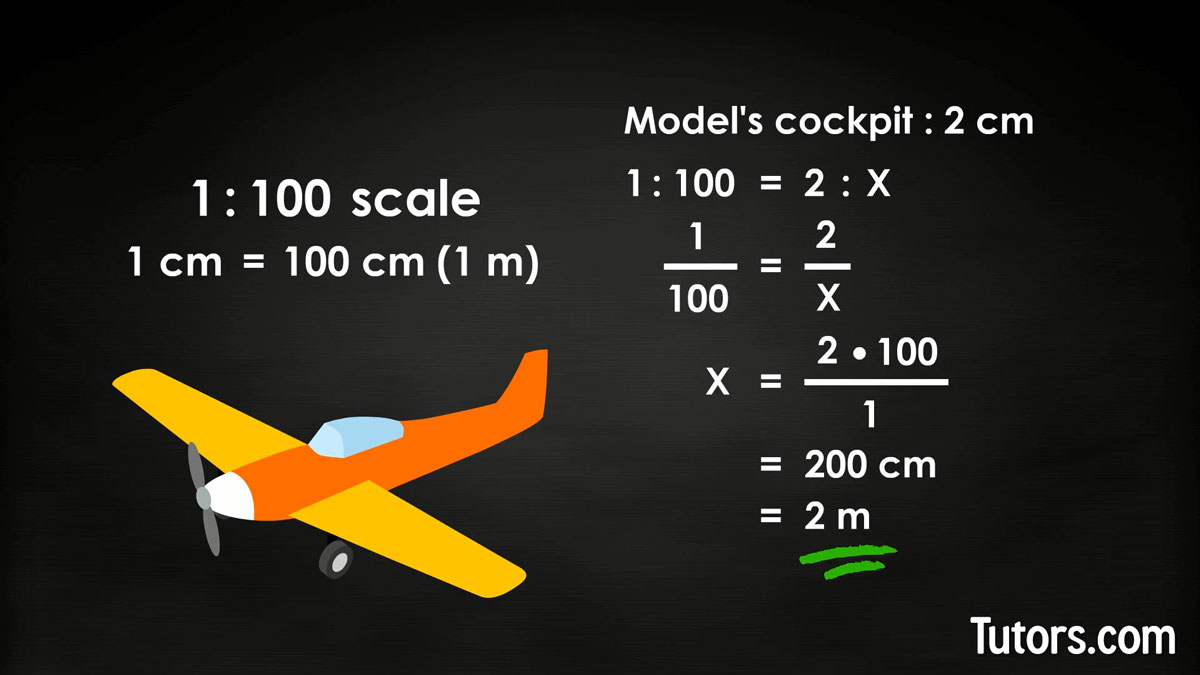
Compare the proportions:
You can quickly see the answer is 200 centimeters, or 2 meters; the real canopy will be 2 meters long.
You can use proportion to check the accuracy of a model. The real aircraft's wheels should measure 50 centimeters (which is the same as 500 mm) in diameter.
How small should the wheels be on the aircraft model? In other words, what is 1/100th of 50 cm?
Let's convert cm to mm and see what it looks like:
Notice the first proportion keeps the original units, cm, so your answer (0.5) will be in centimeters: 0.5 cm, which is 5 mm.
The other two ratios use the converted unit, mm. What would you multiply 100 times to get 500? You would multiply it times 5, so multiply the 1 x 5; the model wheels should be 5 mm in diameter.
Lesson summary
This lesson showed you the definition of proportion, gave you examples of proportions in everyday situations, and taught you how to keep images, scale models and copies of objects in proportion as you increase or decrease their sizes.
You are also now able to find an unknown dimension of an object that is in proportion to another version of the same object (like a television screen, photograph, framed picture, or scale model).