Scale Factor — Definition, Formula & How To Find

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Scale factor definition

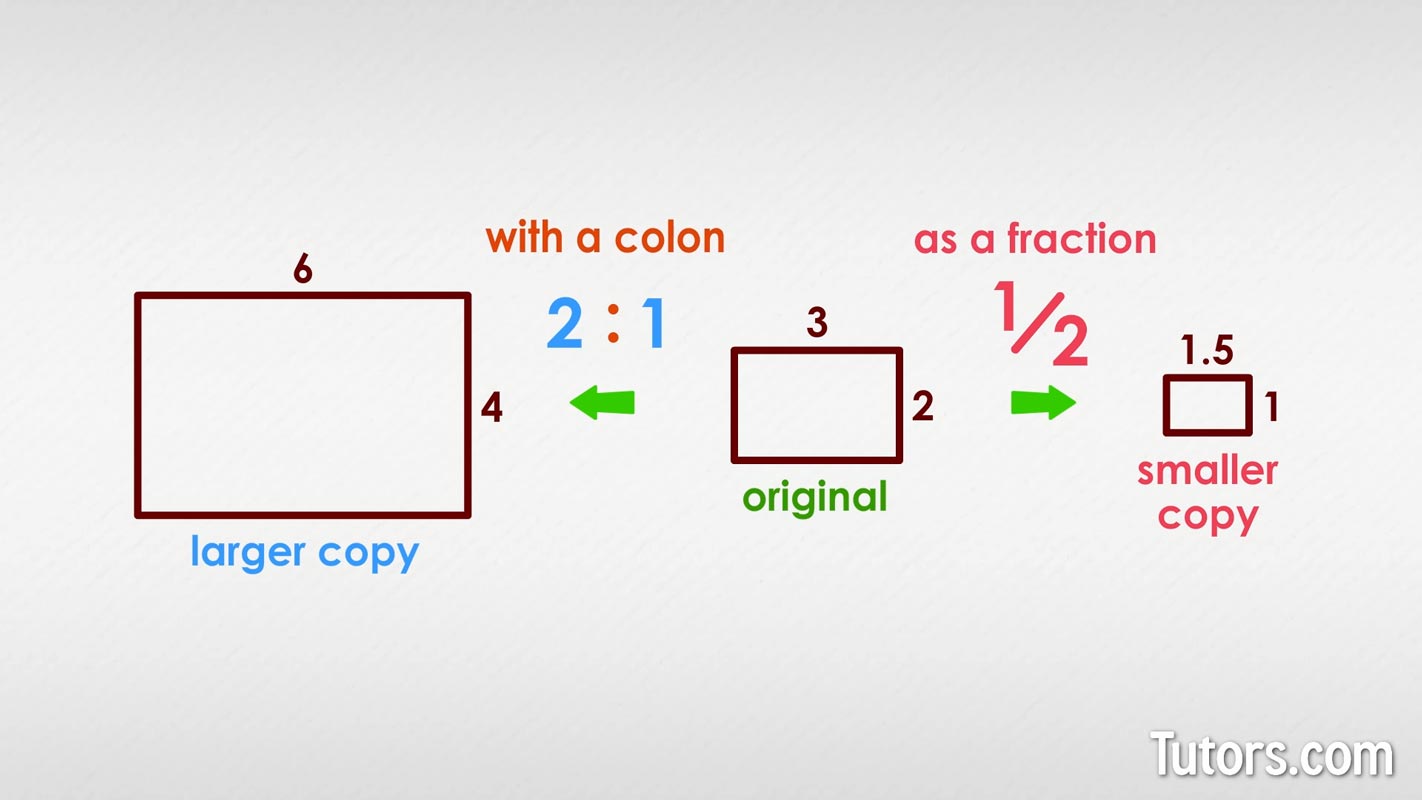
A scale factor in math is the ratio between corresponding measurements of an object and a representation of that object. If the scale factor is a whole number, the copy will be larger. If the scale factor is a fraction, the copy will be smaller.

A scale factor ratio can be expressed as a fraction, $\frac{1}{2}$, or a colon, 1:2.

How to find scale factor

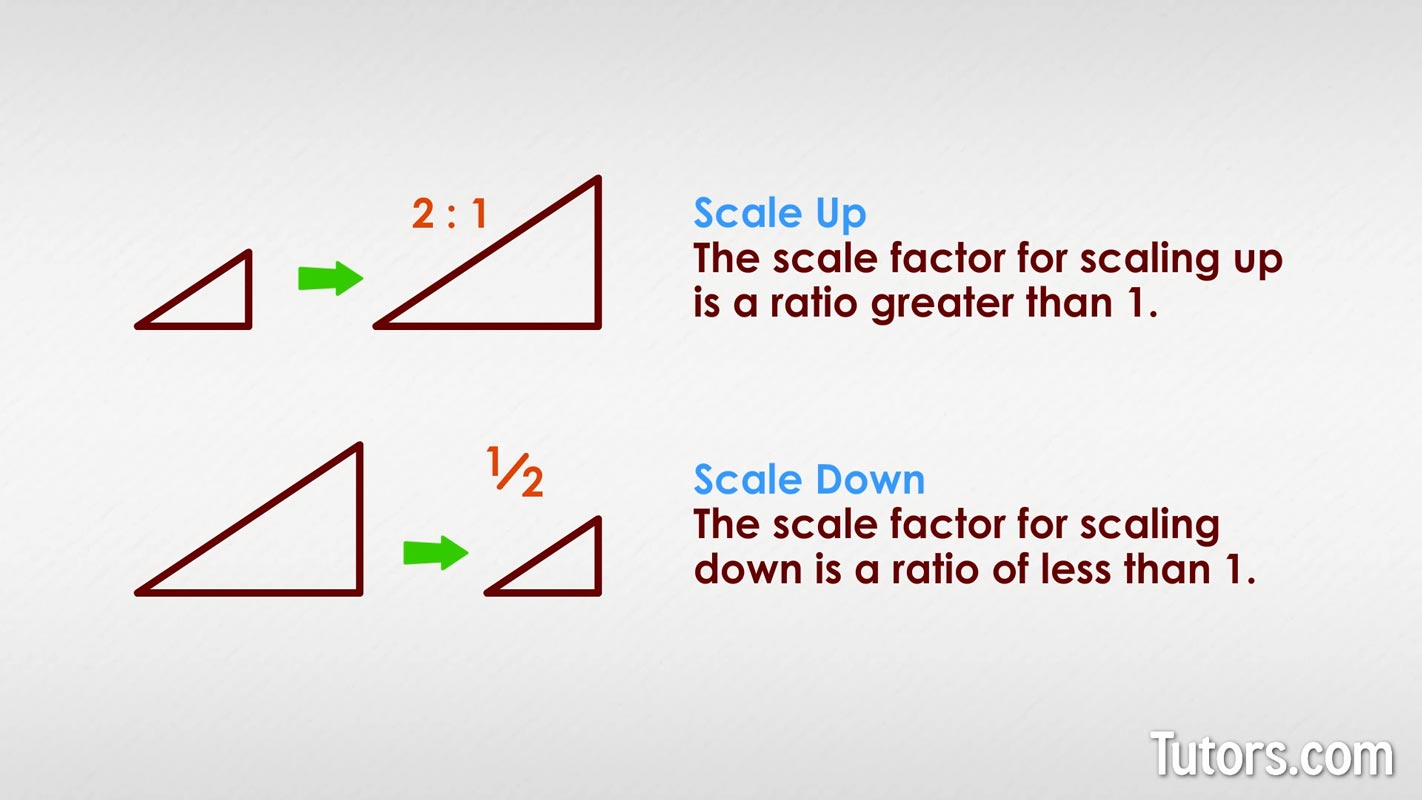
To find the scale factor, you first decide which direction you are scaling:

• Scale Up (smaller to larger) = larger measurement / smaller measurement

• Scale Down (larger to smaller) = smaller measurement / larger measurement

The scale factor for scaling up is a ratio greater than 1.

The scale factor for scaling down is a ratio less than 1.

Once you know which way you are scaling, you compare corresponding sides using the correct basic equation. Compare the side length of the real object to the length of the corresponding side in the representation.

Finding scale factor of similar figures

Here are two similar triangles. What is the scale factor used to create the second, larger figure?

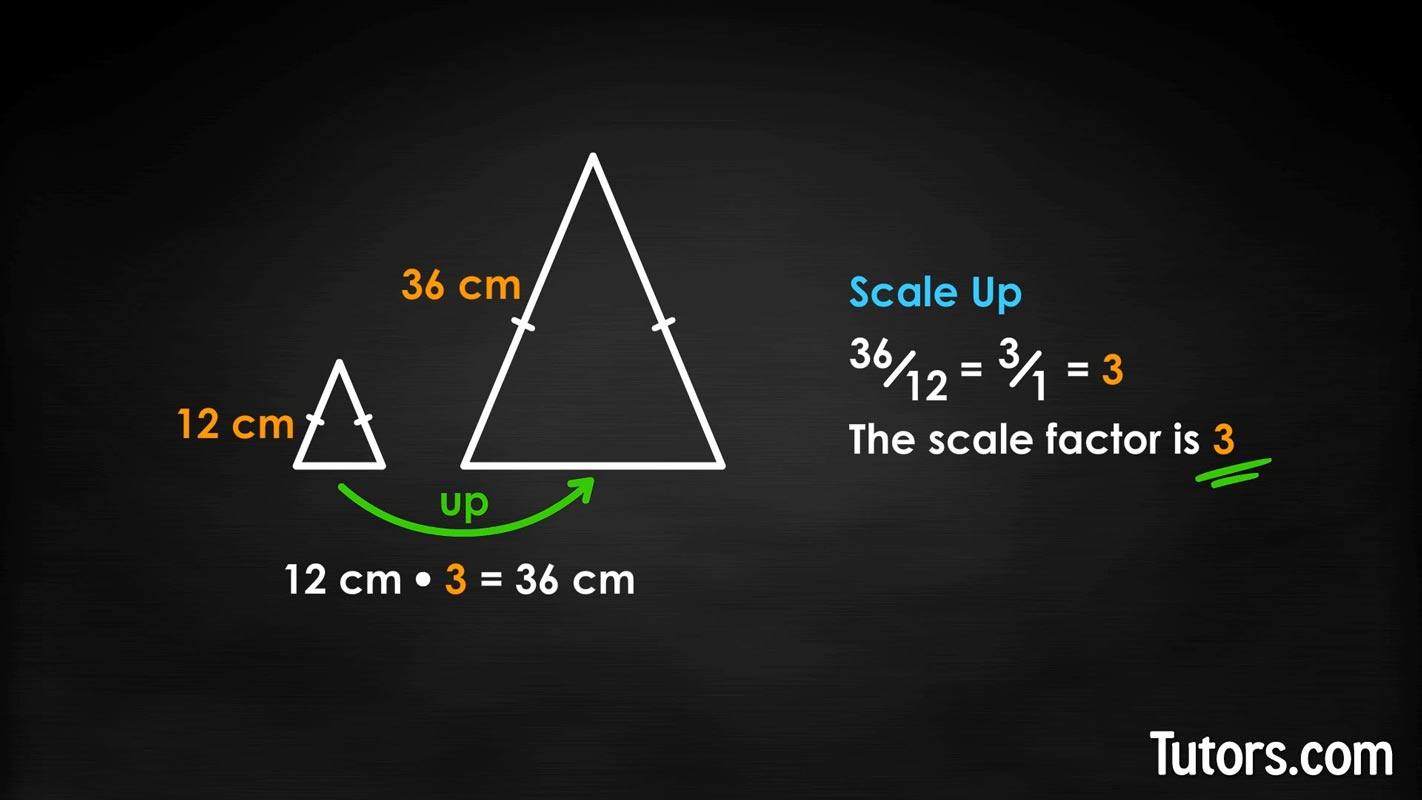
Since we are scaling up, we divide the larger number by the smaller number:

The scale factor is 3. To go from legs of 12 cm to legs of 36 cm, we needed to multiply 12 cm times 3.

Now, let's try to scale down. Here are two similar pentagons. What is the scale factor used to create the second, smaller figure?

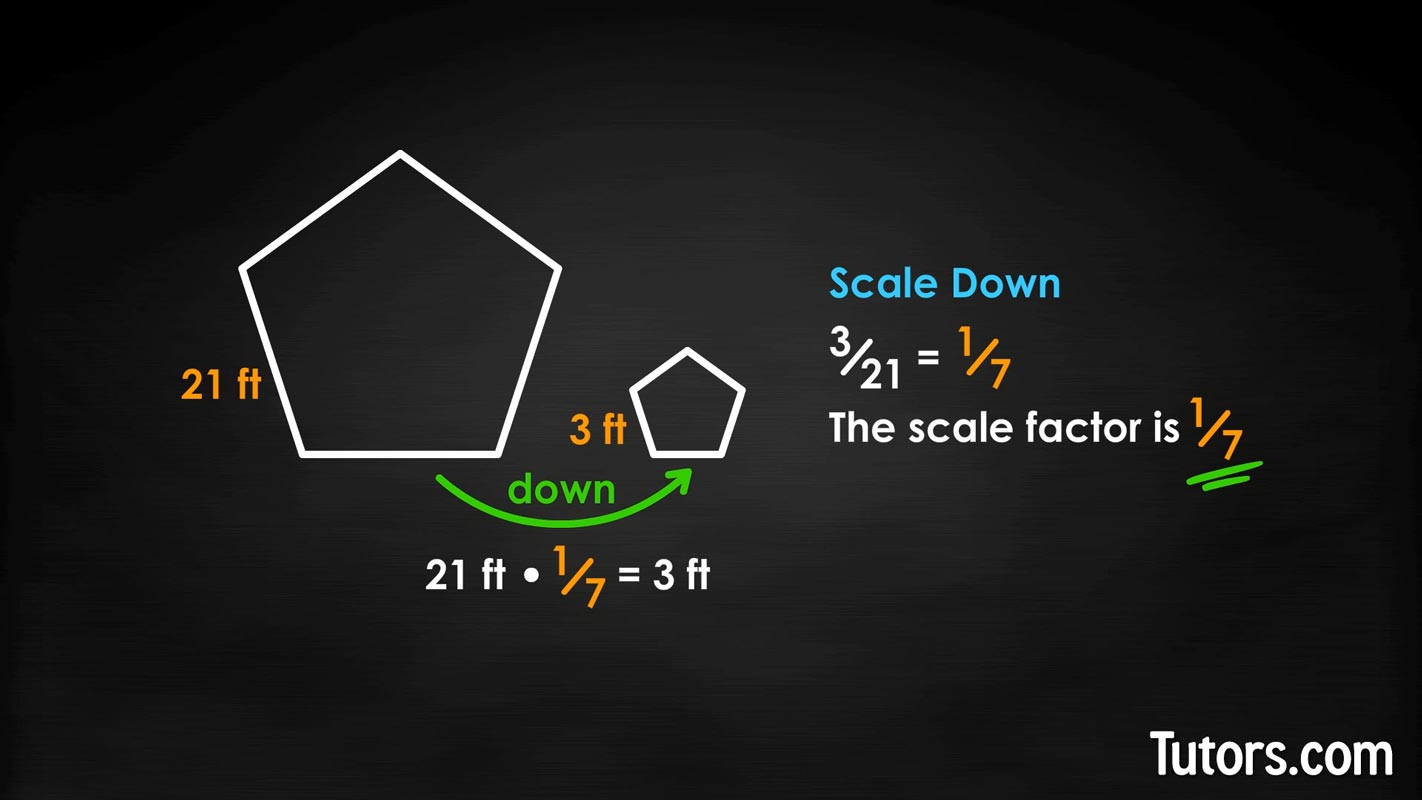
Because we are scaling down, we divide corresponding side lengths (smaller number by larger number):

The scale factor is $\frac{1}{7}$. To get the second, smaller figure, we multiply $21\times \frac{1}{7}$; the figure on the right uses a scale factor of 1:7, $\frac{1}{7}$, or one−seventh.

Let's look at one more example and scale both up and down. Consider these two similar right triangles with labeled sides.

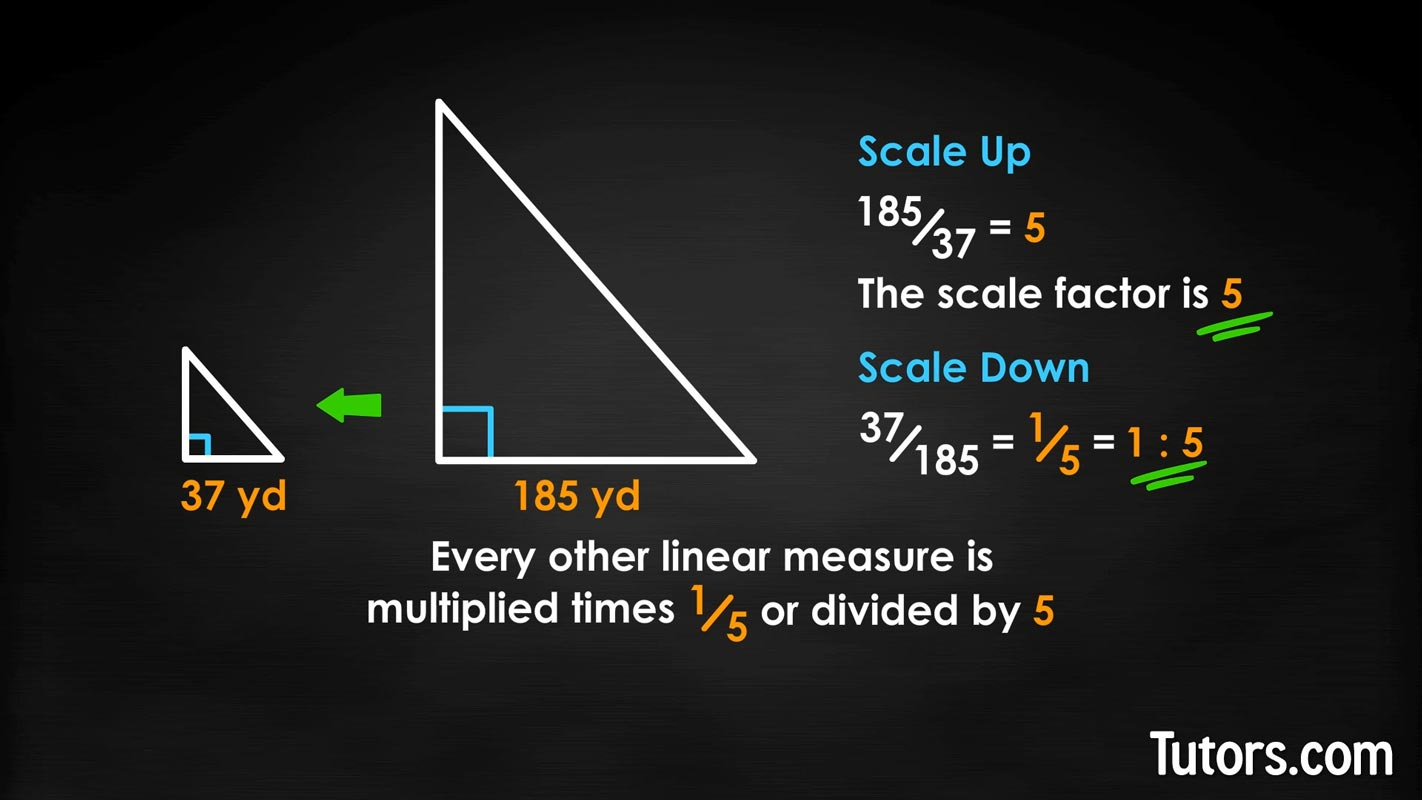
If we have the little right triangle above and want to scale it up to the larger triangle, we write this:

The scale factor of the right triangle is 5:1. So every other linear measure is multiplied by 5 to scale them up.

If we have the big right triangle and want to scale it down to make the smaller one, we write this:

The scale factor of the right triangle is 1:5. So every other linear measure is multiplied by $\frac{1}{5}$ to scale them up.

Scale factor in geometry

Scale is used in geometry to make accurate reproductions of figures; they are different sizes but not proportion. Figures are similar but to scale.

Scale factor is used on similar geometric figures. You can find the scale factor of corresponding angles, sides, and even diagonals.

How to reduce a shape by a scale factor?

Suppose you are given a figure and told to reduce it by 25%. Think in steps:

1. Are you making a larger or smaller dilation?

2. You are shrinking the original, so your scale factor will be less than a whole number.

3. Next, measure (or read) any side of the figure and do some math.

Suppose we have a rectangle that is 16 in. wide and we need to reduce it by 25%, or one-quarter ($\frac{1}{4}$).

That means it will be 75% of the original (100% − 25% = 75%). We will use or 3:4 as our scale factor.

Multiply 16 × $\frac{3}{4}$:

Now, we simplify our answer:

The width of our smaller new shape must be 12 in.. We repeat these steps with the other dimension, 6 in.:

Simplify:

The height of our smaller rectangle must be 4.5 inches.

How to make a scale model

A scale model is a model accurate to a scale factor. If the copy of the actual object is not made to scale, it will look unrealistic, like a little child's toy.

One object can have different scales too. The greater the difference between the two numbers of the ratio, the smaller the model will be. A model that is 1:87 is generally going to be a lot smaller than a model with a ratio of 1:12.

To make scale models, you need accurate plans of the original item, like a scale drawing. A scale drawing is an accurate plan of the real object, drawn using a scale factor to make the drawing small enough to handle.

You multiply every printed dimension on the scale drawing by your scale factor to get the right sizes for model parts. If, for instance, you wanted to build a simple shed for your model railroad scene, you would use the ratio $\frac{1}{87}$, so a 32-foot long shed would come out 4.4 inches long!

Scale factor examples

Try your hand at these questions to see if you understand the concept of scale factor in mathematics. Don’t shrink from it! Make an outsized effort!

1. What is the definition of scale factor?

2. How do you find the scale factor of similar figures?

3. What information does a scale factor give?

4. Define a scale drawing.

Please do not peek ahead until you try your best to find the answers.

1. The definition of scale factor is that it is a number that multiplies times a given quantity to produce a smaller or larger version of the original number. It is the ratio of a drawing, map, model, or blueprint to the actual object or distance.

2. You calculate the scale factor of similar figures by taking the ratio of corresponding parts of the two figures. When enlarging the shape, the larger measurement is the numerator, and the smaller measurement is the denominator. When shrinking the shape, the smaller measurement is the numerator, and the larger measurement is the denominator.

3. A scale factor gives the ratio of the representation to the actual object.

4. A scale drawing is an accurate drawing of an object done using a scale factor to shrink the original object's dimensions.

How to use scale factor

Scaling an object helps you visualize large real-world objects in small spaces or enlarge a small object for better viewing. Scale factor is how we ensure the representation of the object differs only in size from the original object.

We use scale to:

• Draw similar figures in geometry

• Make scale models

• Draw scale blueprints of architecture and machinery

A common real-world use of scale factor is to bring vast areas of land down to small pieces of paper, like on a map.

Scale is used to allow designers, architects, and machinists to handle models of objects that would be too big to keep on a if they were actual size.