How to Find the Perimeter of a Polygon
Is it a polygon?
Have you ever walked around a polygon? Probably not, since all polygons are two-dimensional and you are a three-dimensional person, but if you have ever walked completely around the outside of a building, you have experienced the perimeter of a polygon.
First, let's make sure you're dealing with a polygon. To be a polygon, your shape must be three things:
It must be two-dimensional, having only height and width
It must be made only with straight sides (no curves)
It must close in a space, like a fence around a horse corral (no gaps)
To be a regular polygon, your polygon must also have all sides equal to each other. It must also have all interior angles equal to one another. That will automatically make the exterior angles to be congruent (equal), too.
Perimeter of a polygon
Perimeter is the distance around the exterior of any shape. You can also easily measure the perimeter of all polygons, whether they are regular or irregular polygons.
Recall that a polygon closes in a space, so it creates an interior and an exterior. Think of the sides of the polygon as fences or walls.

Imagine yourself as a little two-dimensional person walking all the way around the polygon. Your trip around the shape is the shape's perimeter.
You start out, running your hand along the exterior of every side, and then you return to your starting point. Whether you realize it or not, you have made one complete rotation, and you have run your hand completely around the perimeter of the polygon.
Suppose, as you stroll around the polygon, you carefully measure each side. When you are done with your rotation around the shape and are back at your starting point, you can add up all those measurements to know the perimeter, in the same linear units used for each side.
You cannot calculate perimeter if you do not know the lengths of all the sides of your polygon. This does not always mean every side will be identified.
For example, in a rectangle, you only need one length and one width, because an identifying property of rectangles is that opposite sides are congruent. If you know those two measurements, you know the lengths of all four sides.
How to find the perimeter of a polygon
Mathematicians have put many of these perimeter measurements into formulas, to speed up calculations. Here are a few, where P is the perimeter:
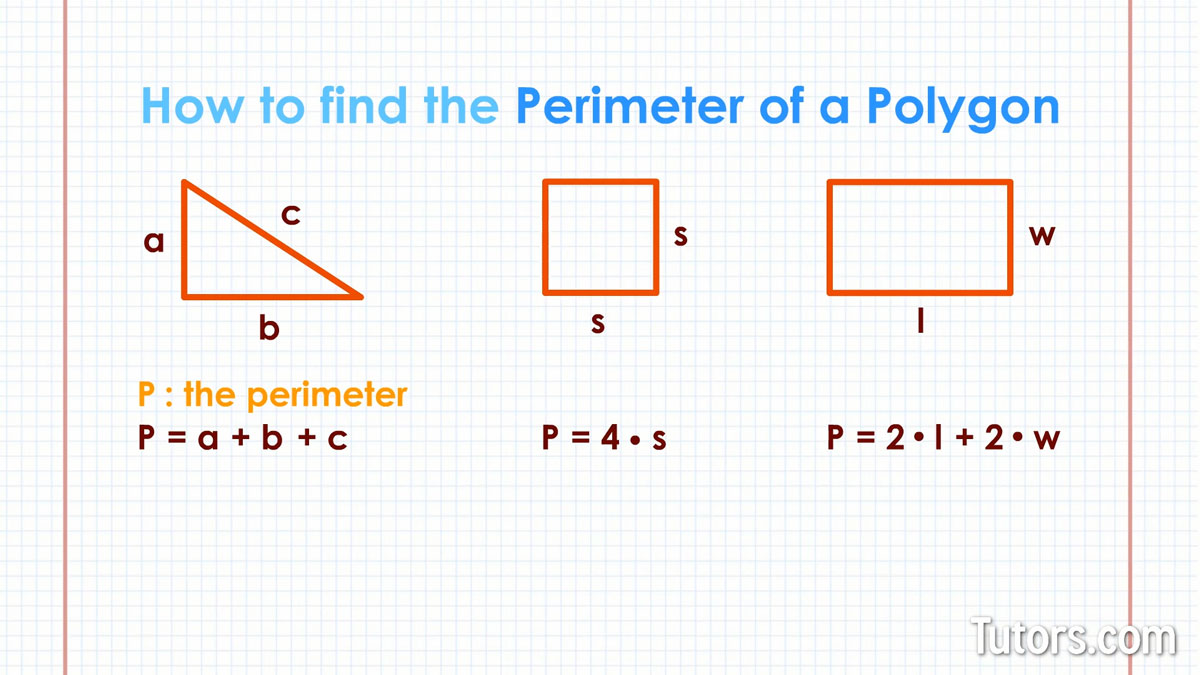
Triangles
For a triangle with sides a, b, c:
Squares
For a square with sides s:
Rectangles
For a rectangle with sides l and w (length and width):
Whatever the unit used for the lengths of sides, that is the same unit for perimeter. So a square with sides of 37 meters has a perimeter of 148 meters.
A triangle with sides 30, 40, and 50 miles has a perimeter of 120 miles.
Applying the perimeter of a polygon formula
Try finding the perimeter yourself! Suppose you are fencing in a rectangular llama pasture that is 200 meters long and 150 meters wide. What is the pasture's perimeter?

Apply the rectangle perimeter formula:
The llama pasture has a perimeter of 700 meters. Perimeter calculations often form the basis for multi-step problems, such as calculating the approximate cost of fencing if you know the price per meter.
Calculating perimeter of irregular polygons
Calculating the perimeter is not always so easy. An irregular polygon that has an unusual shape may require a lot of addition.
Suppose you are in charge of making decorations for a softball team's Championship awards banquet. You make an oversize home plate and need to put a string of decorative lights around its edges. Here is your home plate decoration:
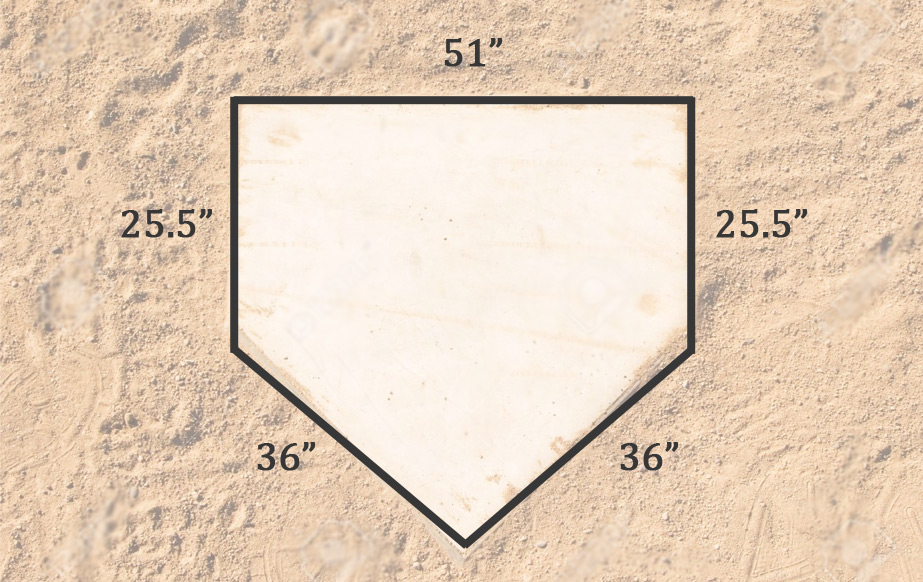
To find the perimeter (for the proper length of lights), add up all the sides:
You need a package of lights at least 14'6" to go completely around the decoration.
How to find the perimeter of a regular polygon
Did you catch our sneaky move in the list of formulas? The square is a regular polygon. It has four equal sides and four equal interior angles.
Its formula is not like the others. For a square, you only needed the length of one side, and then you multiplied by the number of sides.
The formula for calculating the perimeter of any regular polygon (from the simple equilateral triangle up to the weirdest n-gon you can imagine) is always the same.

For a regular polygon with n sides and the length of one side s:
Remember the unit of perimeter will be same linear unit used to measure the polygon's sides. For a regular enneagon (nine-sided polygon) with one side 51 centimeters, the formula would look like this:
Only after calculating the perimeter in the same units as the sides should you attempt to convert the measurement units, if needed: 459 cm = 4.59 m; 4 meters, 59 centimeters; or 4,590 mm.
Lesson summary
After going through the video, graphics and text, you are now able to identify a polygon based on its properties, find the perimeter of any polygon by adding the lengths of all the polygon's sides, and apply knowledge of regular polygons to calculate perimeter quickly, using the formula