How to Find the Area of Regular Polygons
Area of a regular polygon
Regular polygons have all straight sides equal in length and all interior angles equal. Finding the area of any regular polygon (the space of the interior) is easy if you know what an apothem is. Read, watch, and learn!
The area of any closed shape is the interior space formed by the shape's sides. Area is always expressed in square units, such as , , .
Regular polygons use line segments that form sides enclosing a space (the polygon's interior). For regular polygons, you need to know the length of only one side, ss, and the number of sides, nn. To work with the apothem of the polygon, you must know the length of a side.
Area of a regular polygon formula
Combine the number of sides, n, and the measure of one side, s, with the apothem, a, to find the area, A, of any regular polygon.

Let's dive into the details:
How to find the apothem
This may be a new word to you, but the apothem (pronounce it like APP-uh-them) is the distance of a perpendicular line from any side of the polygon to its center.
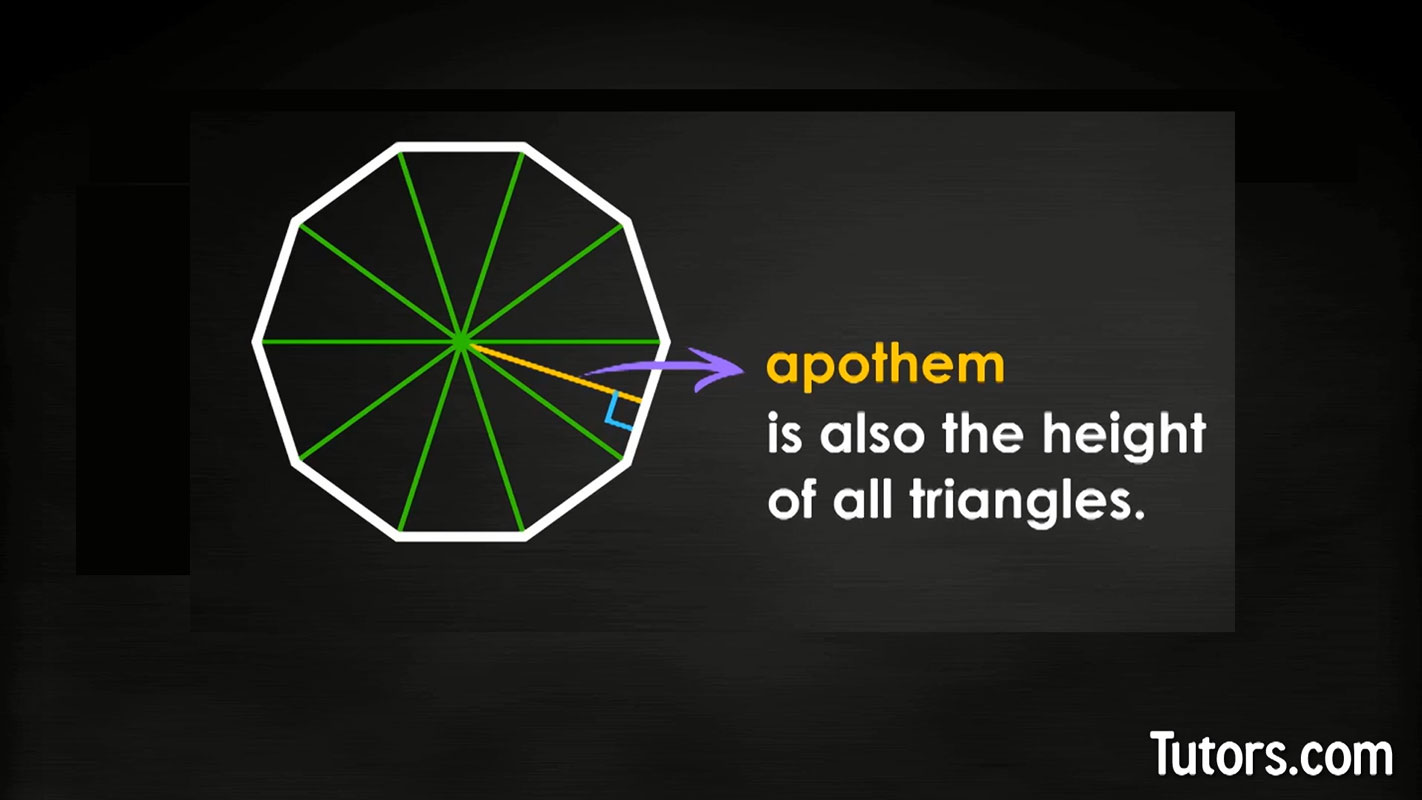
Regular polygons are the only geometric figures that have apothems. The apothem is also the radius of a circle that can be drawn completely inside the regular polygon. That circle is also called the incircle, and its incenter is the center of the regular polygon.
Finding the center
To find the center or incenter of a regular polygon, connect opposite vertices using diagonals. Any two crossing diagonals will locate the center, but you can triple-check by drawing in additional diagonals. Here is a decagon or 10-gon with all five diagonals drawn in:
Notice all five diagonals create 10 small triangles. Drawing a line from the center or incenter to any side of the regular polygon gives you the apothem. It is also the altitude or height of all those triangles.
Apothem area formula
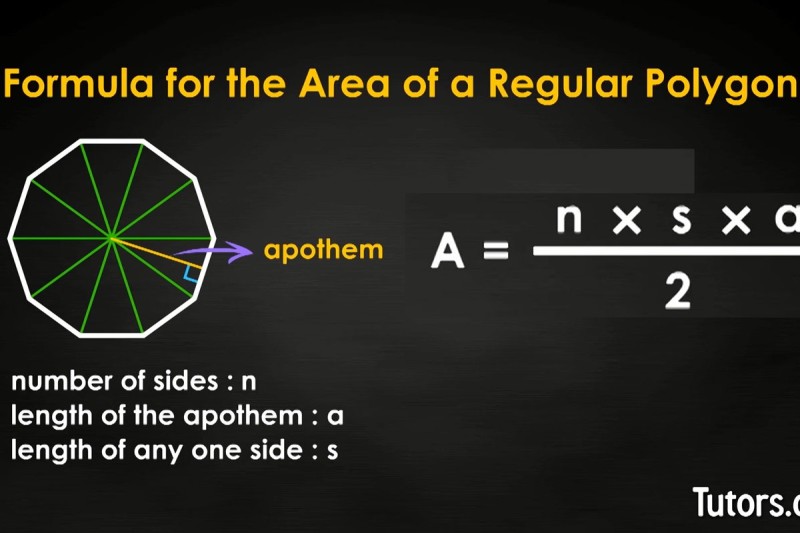
You must know these three facts about your regular polygon:
The number of sides, n
The length of the apothem, a
The length of any one side, s
If you know all three numbers, you can find the area, A, by applying this formula:
How to find the area of a regular polygon
Let's say you have that regular decagon (10 sides; n = 10) with sides, s, 8 meters in length and an apothem, a, of 12.31 meters.
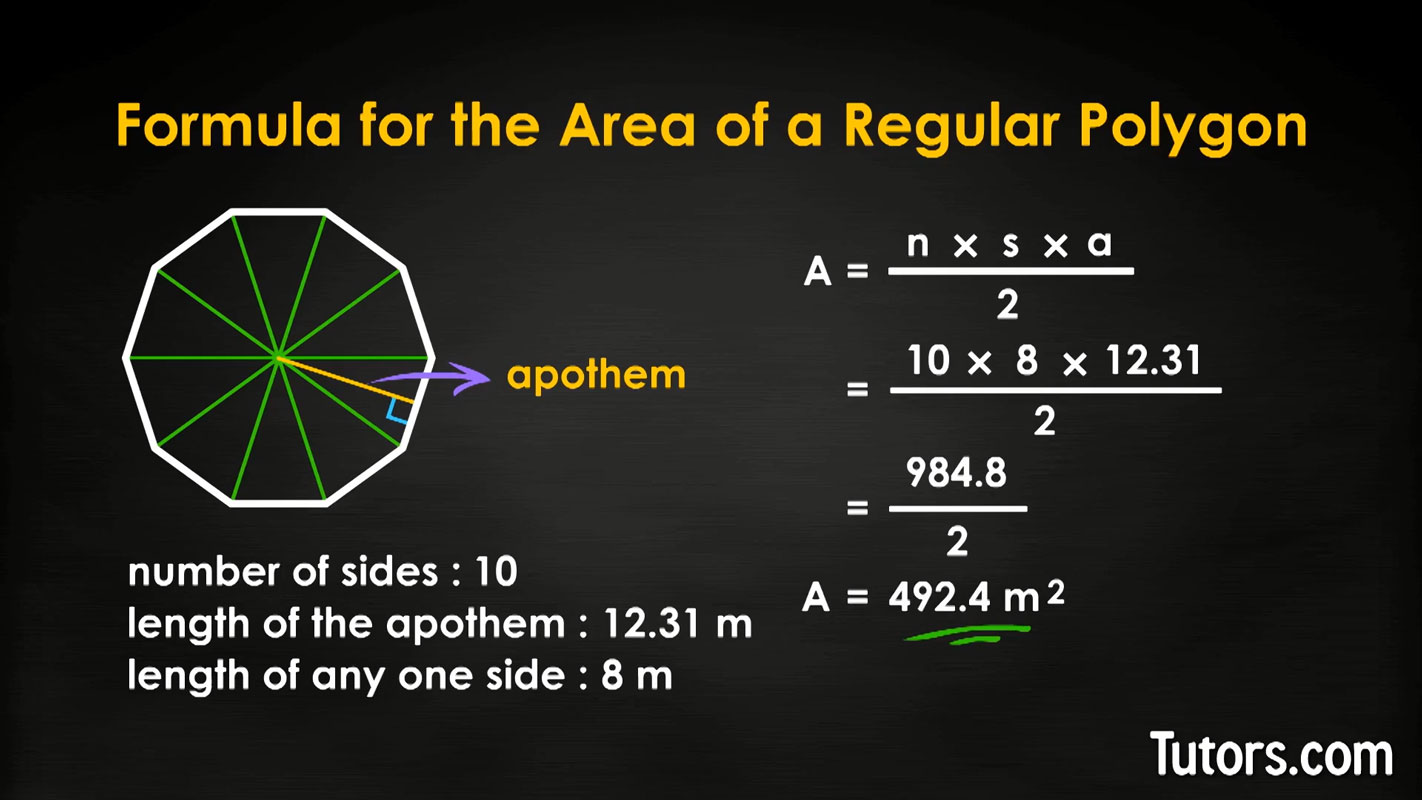
Let's put those numbers into the formula:
The area of our decagon is .
Area of a regular polygon examples
Here is an easier shape to work with. Consider a regular octagon (8 sides; n = 8) with sides 20 centimeters in length. The apothem is 24.142 centimeters. What is the area?
Try it yourself before looking at the steps below.
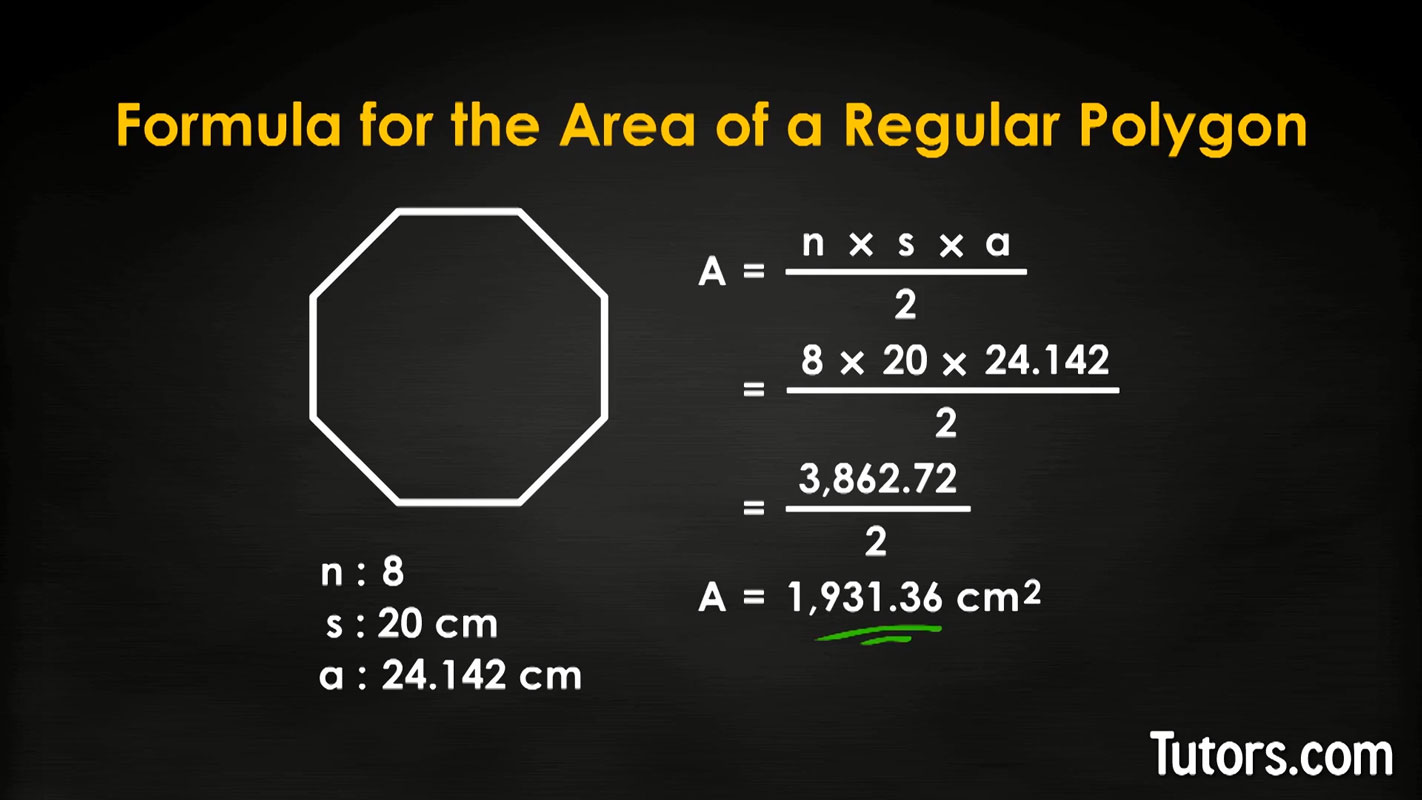
Did you get the area of ?
Lesson summary
You have learned to define and identify a regular polygon, including its parts such as sides and area. You learned what an apothem is, and how to find it on any regular polygon. You also learned the formula for finding the area of any regular polygon if you know the length of one side and the apothem: , where n is the number of sides, s is the length of one side, and a is the apothem.