Arc Measure — Formula, Definition & How to Find

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Arc measure definition

An arc is a segment of a circle around the circumference. An arc measure is an angle the arc makes at the center of a circle, whereas the arc length is the span along the arc. This angle measure can be in radians or degrees, and we can easily convert between each with the formula $\pi$ radians = 180°

You can also measure the circumference, or distance around, a circle. If you take less than the full length around a circle, bounded by two radii, you have an arc. That curved piece of the circle and the interior space is called a sector, like a slice of pizza. When you cut up a circular pizza, the crust gets divided into arcs.

Arc of a circle

If we cut across a delicious, fresh pizza, we have two halves, and each half is an arc measuring 180°. If we make three additional cuts in one side only (so we cut the half first into two quarters and then each quarter into two eighths), we have one side of the pizza with one big, 180° arc and the other side of the pizza with four, 45° arcs like this:

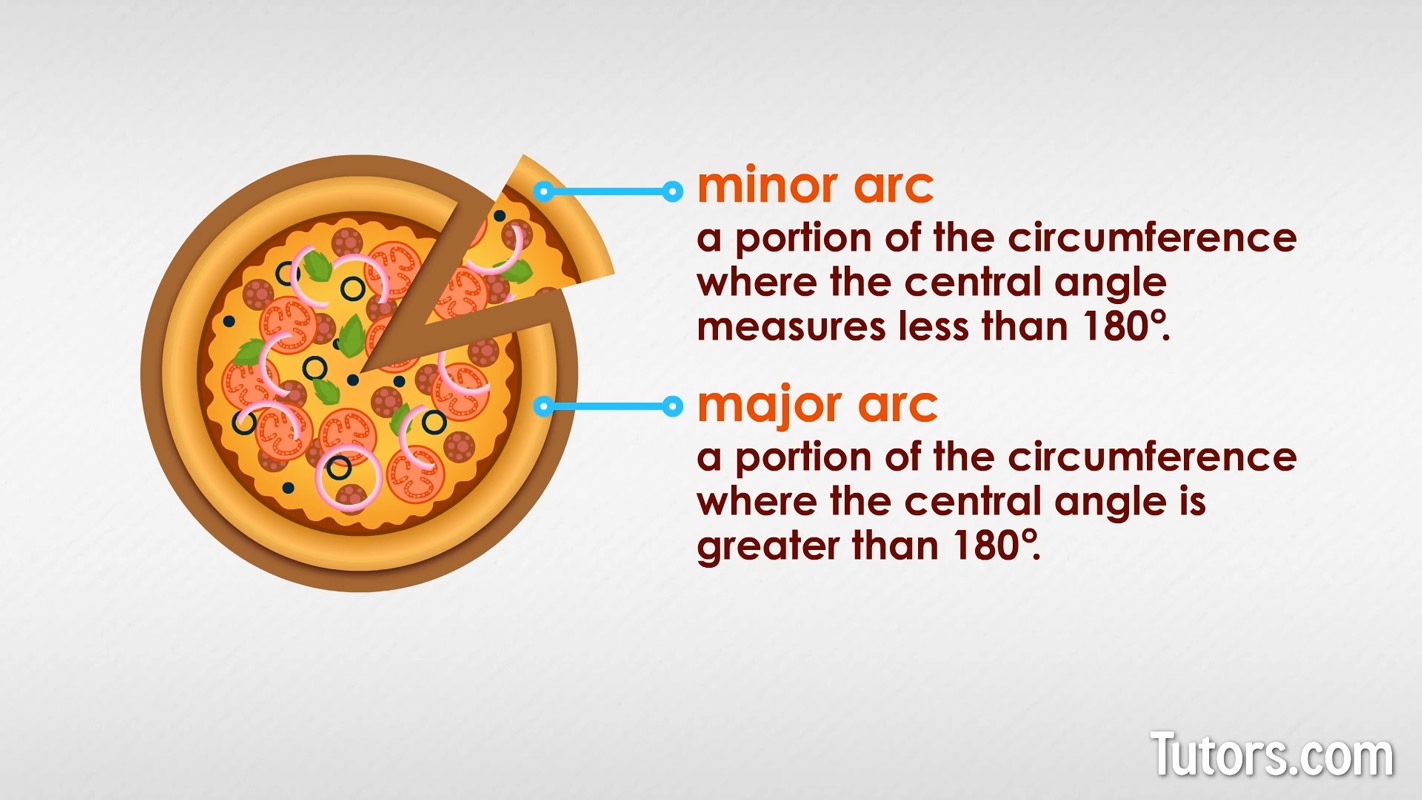
The half of the pizza that is one giant slice is a major arc since it measures 180° (or more). The other side of the pizza has four minor arcs since they each measure less than 180°.

Arc measure vs. arc length

The arc is the fraction of the circle's circumference that lies between the two points on the circle. An arc has two measurements:

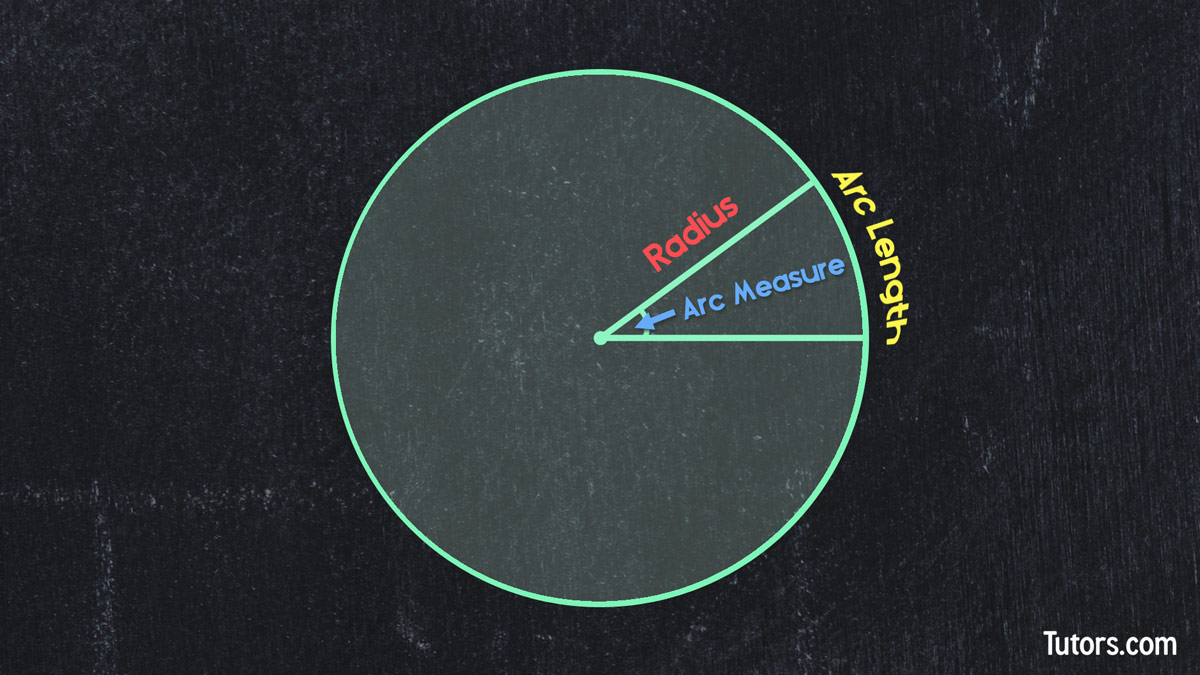
1. The arc's length is a distance along the circumference, measured in the same units as the radius, diameter or entire circumference of the circle; these units will be linear measures, like inches, cm, m, yards, and so on

2. The arc's angle measurement, taken at the center of the circle the arc is part of, is measured in degrees (or radians)

Do not confuse either arc measurement (length or angle) with the straight-line distance of a chord connecting the two points of the arc on the circle. The chord's length will always be shorter than the arc's length.

Degrees and radians

To be able to calculate an arc measure, you need to understand angle measurements in both degrees and radians. An angle is measured in either degrees or radians. A circle measures 360 degrees, or $2\pi$ radians, whereas one radian equals 180 degrees. So degrees and radians are related by the following equations:

The relationship between radians and degrees allows us to convert to one another with simple formulas. To convert degrees to radians, we take the degree measure multiplied by pi divided by 180.

Let's convert 90 degrees into radians for example:

Now let's convert $\frac{\pi }{3}$ radians to degrees:

Arc measure formula

Once you got the hang of radians, we can use the arc measure formula which requires the arc length, s, and the radius of the circle, r, to calculate.

How to find the measure of an arc

Let's try an example where our arc length is 3 cm, and our radius is 4 cm as seen in our illustration:

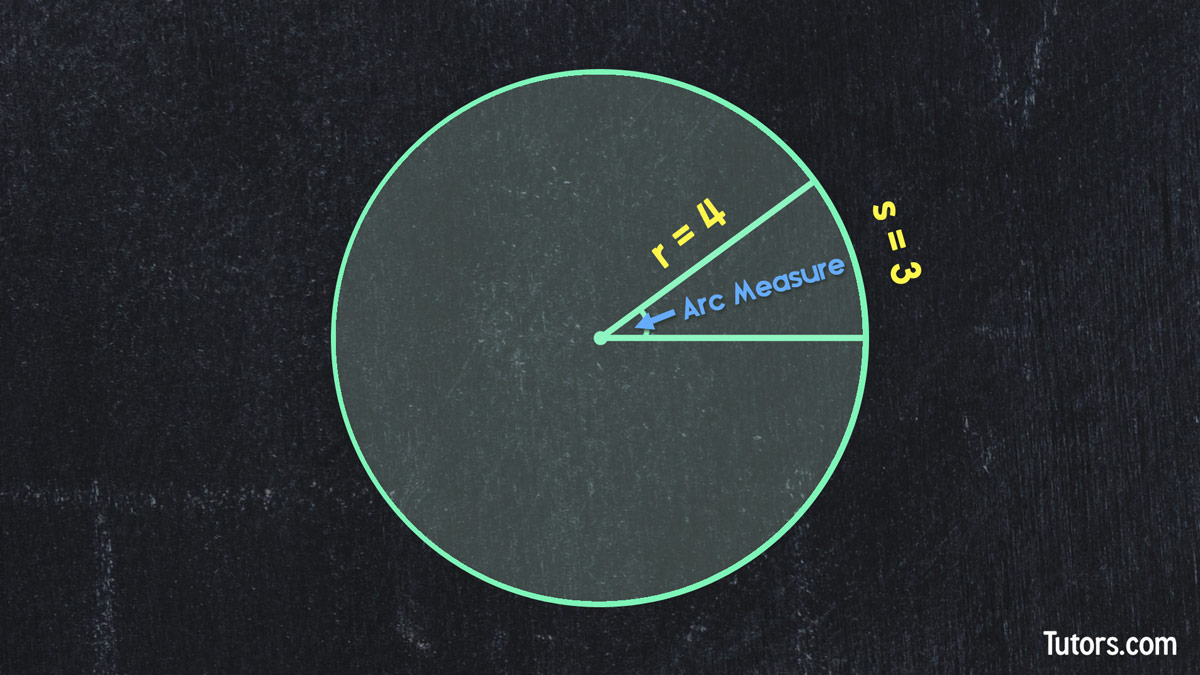
Start with our formula, and plug in everything we know:

Now we can convert $\frac{3}{4}$ radians into degrees by multiplying by 180 dividing by $\pi$.

How to find arc length

You need to know the measurement of the central angle that created the arc (the angle of the two radii) to calculate arc length. The arc length is the fractional amount of the circumference of the circle. The circumference of any circle is found with $2\pi r$ where r = radius. If you have the diameter, you can also use $\pi d$ where d = diameter.

The formula for finding arc length is:

Let's try an example with this pizza:

Our pie has a diameter of 16 inches, giving a radius of 8 inches. We know the slice is 60°. So the formula for this particular pizza slice is:

Identifying arc angle indicated

An arc angle's measurement is shown as $m\overset\frown{AB}$ where A and B are the two points on the circle creating the arc. The mm means measurement, and the short curved line over the $\overset\frown{AB}$ indicates we are referring to the arc. The two points derived from the central angle (the angle of the two radii emerging from the center point).

One important distinction between arc length and arc angle is that, for two circles of different diameters, same-angle sectors from each circle will not have the same arc length. Arc length changes with the radius or diameter of the circle (or pizza).

Lesson summary

Now that you have eaten your way through this lesson, you can identify and define an arc and distinguish between major arcs and minor arcs. You are also able to measure an arc in linear units and degrees and use the correct symbol, $m\overset\frown{AB}$ (where A and B are the two points on the circle), to show arc length.