Converse of The Pythagorean Theorem

Table of Contents

1. Definition
2. Pythagorean Theorem
3. The Law of Cosines
4. Converse Of The Pythagorean Theorem
5. Applying The Converse

What is the Converse of The Pythagorean Theorem?

The Pythagorean Theorem allows you to find the length of any side of a right triangle if you know the lengths of the other two sides. It can be viewed in another way, as the Converse Of The Pythagorean Theorem, to determine if a given triangle is a right triangle just by knowing the lengths of its three sides.

Pythagorean Theorem

To understand the converse of the Pythagorean Theorem, you need to know and recall the Pythagorean Theorem itself:

This formula works for any right triangle $ABC$ where $a$ and $b$ are legs and $c$ is the hypotenuse. The theorem works for all right triangles, so if you know any two lengths (say, $a$ and $c$), you can find the unknown length (in our example, $b$). That is a useful application of the Pythagorean Theorem.

The Law of Cosines

Before we leap ahead, let's make sure we see the special application of the Law of Cosines in the Pythagorean Theorem.

First, here is the Law of Cosines for $△ABC$ where $a$ and $b$ are legs and $c$ is the hypotenuse, with $\angle C$ the right angle opposite the hypotenuse:

$a^2 + b^2 - 2 \times a \times b \times \cos \left(\angle C\right) = c^2$

$a^2 + b^2 - 2 ab \times \cos \left(\angle C\right) = c^2$

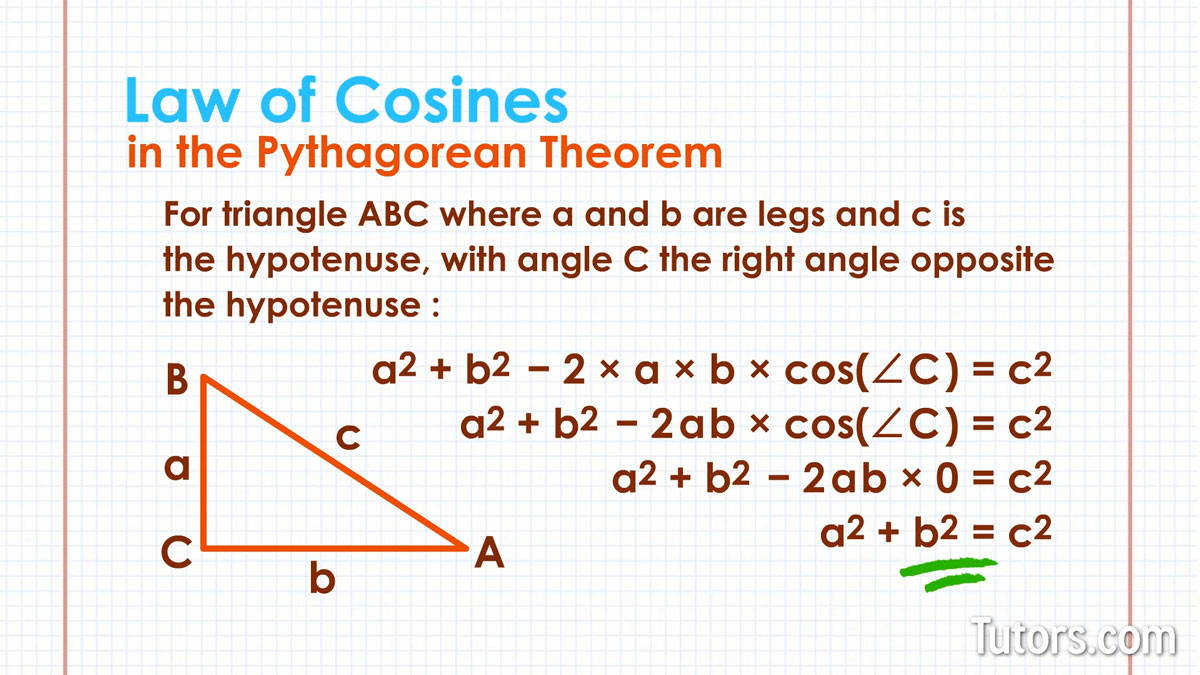
The cosine of $90°$ is 0, which leaves you with $2ab \times 0$, so the entire expression, $2ab \cos \left(\angle C\right) = 0$ and can be removed, leaving just the Pythagorean Theorem:

$a^2 + b^2 - \mathbf{2}\mathbf{ab} \mathbf{cos}\left(\mathbf{\angle }\mathbf{C}\right) = c^2$

$a^2 + b^2 - 0 = c^2$

$a^2 + b^2 = c^2$

Converse Of The Pythagorean Theorem

Suppose, though, we start at the "other end." We have three sides $a$, $b$, and $c$, but are not certain $△ABC$ is a right triangle. In that case, we can apply the Converse Of The Pythagorean Theorem, which states:

Applying the Converse Of The Pythagorean Theorem

Suppose you are given the lengths of three sides of a triangle and asked to determine if it is a right triangle. A common reason for this might be in architecture or in engineering, like getting the correct length of guy-wires bracing an important bridge. Right angles in engineering are very strong.

You know the three sides (legs $a$ and $b$, hypotenuse $c$) are as follows:

$a = 56$

$b = 192$

$c = 200$

If $a^2 + b^2 = c^2$, then the triangle has to be a right triangle and the guy-wires have to be the perfect and safe length to hold up the bridge.

So you put the three lengths into the Pythagorean Theorem formula:

$a^2 + b^2 = c^2$

${56}^2 + {192}^2 = {200}^2$

$\mathrm{3,136} + \mathrm{36,864} = \mathrm{40,000}$

$\mathrm{40,000} = \mathrm{40,000}$

What a relief! The guy-wires are all the correct length to keep the bridge at a safe, sturdy right angle.

Lesson Summary

Today you reviewed what the Pythagorean Theorem is and why it is useful, how to write and use the formula for the Pythagorean Theorem ($a^2 + b^2 = c^2$), and learned how the Pythagorean Theorem is one application of the Law of Cosines.

You also learned what the Converse Of The Pythagorean Theorem is; namely, any triangle in which the square of the longest side of a triangle is equal to the sum of the squares of the other two sides must be a right triangle.

Next Lesson:

Pythagorean Triples