20+ tutors near you & online ready to help.

TABLE OF CONTENTS

Area of a Semicircle — Formula, Definition & Perimeter

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Semicircle definition

A semicircle is a half circle. That means a semicircle will have half of the area of a circle. You might think that means it will have half the perimeter of a circle, but that is not true.

To make a semicircle, take any diameter of the circle. Remove one half of the circle along that diameter. You have a semicircle (half of a circle).

A semicircle is half the circumference of a full circle plus the diameter of a circle, d:

Learn about the radius, diameter, and circumference of a circle in this lesson.

Get free estimates from geometry tutors near you.

Area of a semicircle

The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape.

The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle.

Area of a semicircle formula

The formula for the area, A, of a circle is built around its radius. You find the area of a semicircle by plugging the given radius of the semicircle into the area of a semicircle formula.

The area formula is:

A=\frac{\pi {r}^{2}}{2}

How to find the area of a semicircle

For example, the semicircle below has a radius of 19 cm. What is the area of the semicircle?

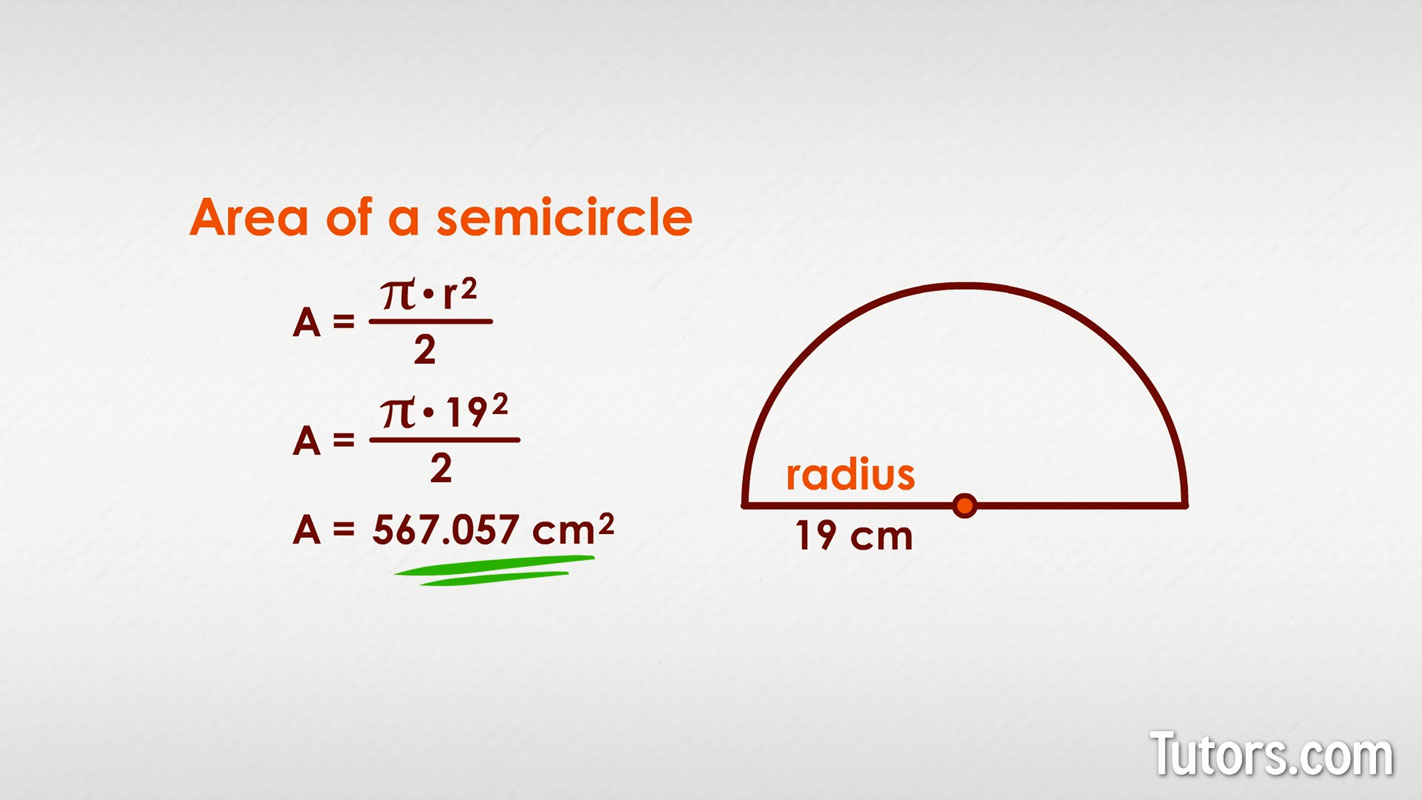
To find its area, we replace r with the actual value:

\mathrm{A}=\frac{{\\pi r}^{2}}{2}

A=\frac{\pi ({19}^{2})}{2}

A=\frac{\pi (361)}{2}

A=\frac{1134.114947}{2}

A=567.057{cm}^{2}

Area of a semicircle examples

The Roman aqueduct of Barcelona in Spain is very old, dating from the first century of the Common Era. The aqueduct is very nearly gone, but it has semicircular arches still visible on a wall in Barcelona.

The arches measure 2.96 meters in diameter. What is the perimeter and area of each arch?

\mathrm{P}=\\pi r+2\mathrm{r}

P=\pi (1.48m)+2.96m

P=4.649557m+2.96m

P=7.609557m

Now, we find the area:

A=\frac{{\\pi r}^{2}}{2}

A=\frac{\pi (1.48{m}^{2})}{2}

A=\frac{6.881344{m}^{2}}{2}

A=3.440672{m}^{2}

Perimeter of a semicircle

The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d. Since the semicircle includes a straight side, its diameter, we cannot describe the distance around the shape as the circumference of a semicircle; it is a perimeter.

How to find the perimeter of a semicircle

Recall that the formula for the perimeter (circumference), C, of a circle of radius, r, is:

C=2\pi r

Another formula that works is:

C=\pi d

To find the perimeter, P, of a semicircle, you need half of the circle's circumference, plus the semicircle's diameter:

P=\frac{1}{2}(2\pi r)+d

The $\frac{1}{2}$ and 2 cancel each other out, so you can simplify to get this perimeter of a semicircle formula.

Perimeter of semicircle formula

P=\pi r+d

Using the substitution property of equality, you can also replace diameter with radius throughout:

$P=\frac{1}{2}(2\pi r)+2r$
$P=\pi r+2r$

Find the perimeter of a semicircle examples

Let's try an example. A semicircle that has a diameter of 100 meters. What is the perimeter?

P=\frac{1}{2}(\pi d)+d

P=\frac{1}{2}(\pi \times 100)+100

P=\frac{1}{2}(314.159265)+100

P=157.079632+100

P=257.08meters

It is fine to round the decimal places as we did here.

Let's try an example using the radius of a semicircle. A semicircle has a radius of 365 inches. What is its perimeter?

P=\pi r+2r

P=\pi r+2r

P=257.08meters

P=1,146.681318+730

P=1,876.68 inches

If the question asks you to convert your answer to units like feet or yards, convert it; otherwise leave it in the original linear units. Round your answer to whatever decimal value the problem requires.

The semicircles at both ends of an NBA basketball court indicate the restricted areas beneath each basket. The semicircles have four-foot radii. What is the perimeter of one semicircle in one restricted area?

P=\pi r+2r

P=\pi (4\text{'})+2(4\text{'})

P=12.56637'+8'

P=20.56637'

In this case, having a measurement to 100,000ths of a foot is unnecessary; 20.57' is a reasonably accurate answer.

Angle inscribed in a semicircle

The angle inscribed in a semicircle is always 90°. The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°.

The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle.