Area of a Sector of a Circle

Table Of Contents

1. Sector of a Circle
2. How to Find Area of a Sector
3. Find the Radius of a Circle
4. Area of a Sector Formula
5. Area of Sector Radians
6. Area of a Sector of a Circle Examples
7. Arc Length and Sector Area

Sector of a Circle

Anytime you cut a slice out of a pumpkin pie, a round birthday cake, or a circular pizza, you are removing a sector. A sector is created by the central angle formed with two radii, and it includes the area inside the circle from that center point to the circle itself. The portion of the circle's circumference bounded by the radii, the arc, is part of the sector.

Arcs of a Circle

Acute central angles will always produce minor arcs and small sectors. When the central angle formed by the two radii is $90°$, the sector is called a quadrant (because the total circle comprises four quadrants, or fourths). When the two radii form a $180°$, or half the circle, the sector is called a semicircle and has a major arc.

Unlike triangles, the boundaries of sectors are not established by line segments. True, you have two radii forming the central angle, but the portion of the circumference that makes up the third "side" is curved, so finding the area of the sector is a bit trickier than finding area of a triangle. The distance along that curved "side" is the arc length.

How to Find Area of a Sector

You cannot find the area of a sector if you do not know the radius of the circle. Be careful, though; you may be able to find the radius if you have either the diameter or the circumference. You may have to do a little preliminary mathematics to get to the radius.

Find the Radius of a Circle

Given the diameter, $d$, of a circle, the radius, $r$, is:

$r=\frac{d}{2}$

Given the circumference, $C$ of a circle, the radius, $r$, is:

$r=\frac{C}{\left(2\pi \right)}$

Once you know the radius, you have the lengths of two of the parts of the sector. You only need to know arc length or the central angle, in degrees or radians.

Area of a Sector Formula

The central angle lets you know what portion or percentage of the entire circle your sector is. A quadrant has a $90°$ central angle and is one-fourth of the whole circle. A $45°$ central angle is one-eighth of a circle.

Those are easy fractions, but what if your central angle of a 9-inch pumpkin pie is, say, $31°$?

[insert drawing of pumpkin pie with sector cut at +/- 31°]

This formula helps you find the area, $A$, of the sector if you know the central angle in degrees, $n°$, and the radius, $r$, of the circle:

For your pumpkin pie, plug in $31°$ and 9 inches:

$A = \left(\frac{31}{360}\right) \times \pi \times 9^2$

$A = 0.086111 \times \pi \times 81$

$\mathbf{A = }\mathbf{21.9126}\mathbf{ }{\mathbf{in}}^{\mathbf{2}}$

Area of Sector Radians

If, instead of a central angle in degrees, you are given the radians, you use an even easier formula.

To find Area, $A$, of a sector with a central angle $\theta$ radians and a radius, $r$:

Our beloved $\pi$ seems to have disappeared! It hasn't, really. Radians are based on $\pi$ (a circle is $2\pi$ radians), so what you really did was replace $\frac{n°}{360°}$ with $\frac{\theta }{2}\pi$. When $\frac{\theta }{2}\pi$ is used in our original formula, it simplifies to the elegant $\left(\frac{\theta }{2}\right) \times r^2$.

Area of a Sector of a Circle Examples

You have a personal pan pizza with a diameter of $30 cm$. You have it cut into six equal slices, so each piece has a central angle of $60°$. What is the area, in square centimeters, of each slice?

$A = \left(\frac{n°}{360°}\right) \times \pi \times r^2$

Try it yourself first, before you look ahead!

$A = \left(\frac{60°}{360°}\right) \times \pi \times {15}^2$

$A = \left(\frac{1}{6}\right) \times \pi \times 225$

$A = 117.8097 c{m}^2$

Area of a Sector Example Using Radians

Suppose you have a sector with a central angle of $0.8$ radians and a radius of $1.3$ meters. Your formula is:

Try it yourself before you look ahead!

$A = \left(\frac{0.8}{2}\right) \times {1.3}^2$

$A = 0.676 m^2$

Arc Length and Sector Area

You can also find the area of a sector from its radius and its arc length. The formula for area, $A$, of a circle with radius, r, and arc length, $L$, is:

Here is a three-tier birthday cake $6$ inches tall with a diameter of $10$ inches.

[insert cartoon drawing, or animate a birthday cake and show it getting cut up]

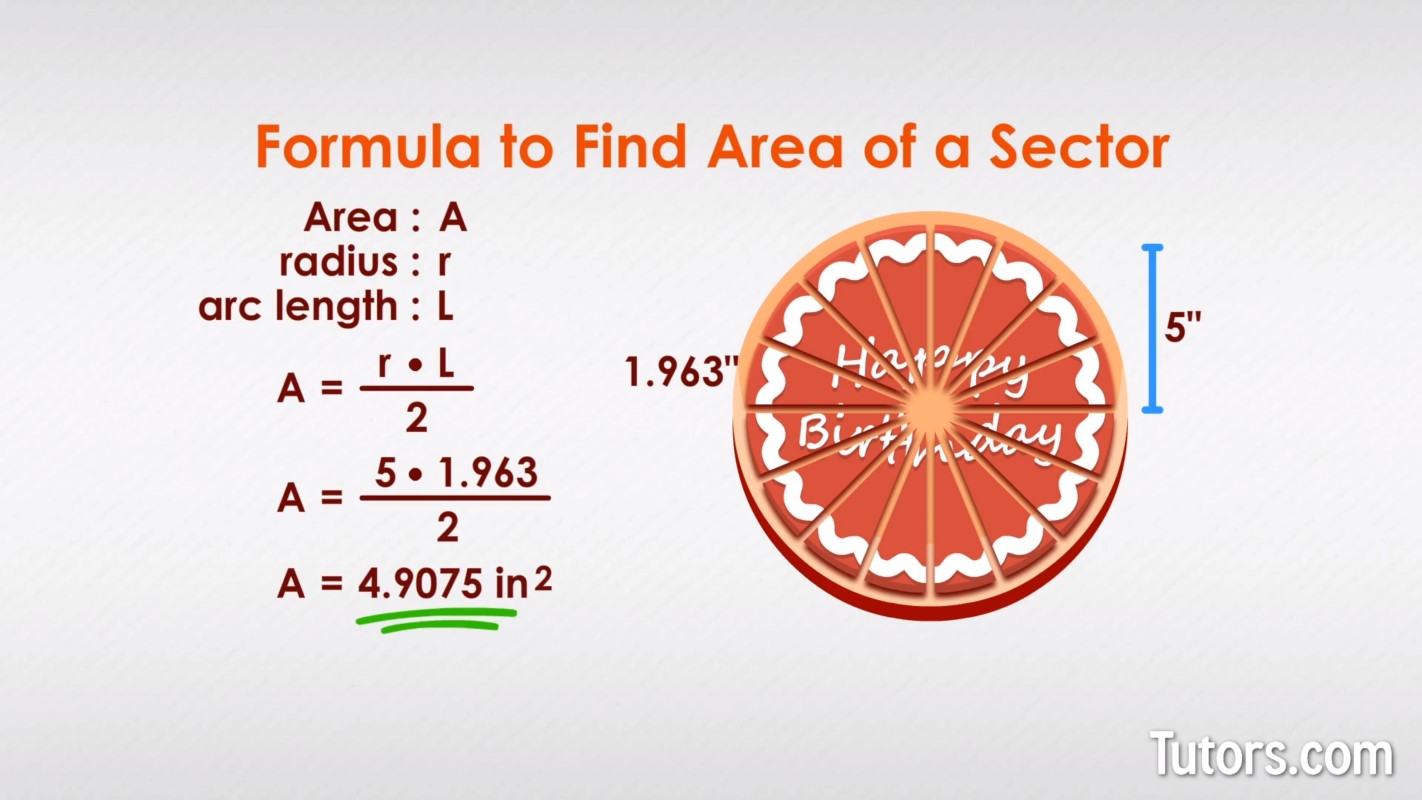
You cut it into $16$ even slices; ignoring the volume of the cake for now, how many square inches of the top of the cake does each person get?

Each slice has a given arc length of $1.963$ inches. The radius is $5$ inches, so:

$A = \frac{(5 \times 1.963)}{2}$

$A = 4.9075 i{n}^2$

Next Lesson:

Equations Of A Circle